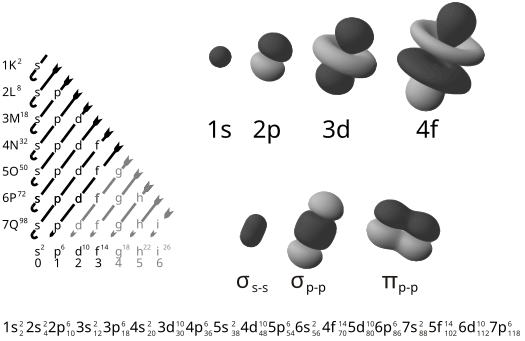
ელექტრონული კონფიგურაცია
|
Read other articles:

Serengan beralih ke halaman ini. Untuk kelurahan yang bernama Serengan, lihat pula Serengan, Serengan, Surakarta.. SerenganKecamatanPeta lokasi Kecamatan SerenganNegara IndonesiaProvinsiJawa TengahKotaSurakartaPemerintahan • Camat-Populasi • Total44,120 (2.001) jiwaKode Kemendagri33.72.02 Kode BPS3372020 Luas3,19 km²Desa/kelurahan7 Serengan (Jawa: ꦱꦼꦫꦺꦔꦤ꧀, translit. Sěrèngan) adalah kecamatan yang terletak di selatan Kota Surakarta d...

Cet article concerne le fantassin de la Grèce antique. Pour le genre d'ammonites, voir Hoplites. Représentation d'un hoplite, Ve siècle av. J.-C. L'hoplite (en grec ancien ὁπλίτης / hoplítēs) est un fantassin de la Grèce antique lourdement armé et organisé en phalange, par opposition au gymnète et au peltaste, équipés plus légèrement. Présent dans chaque cité-État à l'époque classique, il représente le soldat grec par excellence. Les hoplites son...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Beatmania European video game – news · newspapers · books · scholar · JSTOR (March 2024) (Learn how and when to remove this template message)2000 video gameBeatmaniaCover artDeveloper(s)KonamiPublisher(s)KonamiPlatform(s)PlayStationReleaseEU: June 2000Genr...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2022) (Learn how and when to remove this message) Cinema of Hong Kong 1909–1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1...

Oberlargcomune Oberlarg – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementAltkirch CantoneAltkirch TerritorioCoordinate47°27′N 7°14′E / 47.45°N 7.233333°E47.45; 7.233333 (Oberlarg)Coordinate: 47°27′N 7°14′E / 47.45°N 7.233333°E47.45; 7.233333 (Oberlarg) Superficie8,11 km² Abitanti157[1] (2009) Densità19,36 ab./km² Altre informazioniCod. postale68480 Fuso orarioUTC+1 Codice ...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) This is a list of National Historic Sites (French: Lieux historiques nationaux du Canada) in Hamilton, Ontario. There are 15 National Historic Sites designated in Hamilton,[1] of which one (HMCS Haida) is administered by Parks Canada (identified below by the beaver icon ).[2] Burlington Heights was designated in 1929 and was the...
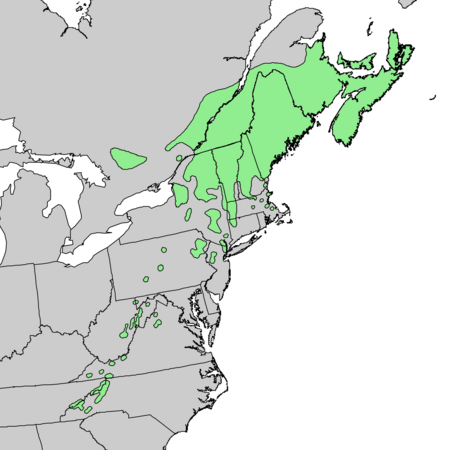
Species of plant Red spruce Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Gymnospermae Division: Pinophyta Class: Pinopsida Order: Pinales Family: Pinaceae Genus: Picea Species: P. rubens Binomial name Picea rubensSarg. Synonyms[2] Abies americana K.Koch nom. illeg. Abies rubra (Du Roi) Poir. Picea americana Suringar Picea australis Small Picea nigra var. rubra (Du Roi) Engelm. Picea rubra (Du ...

1956 film by Daniel Mann The Teahouse of the August MoonTheatrical release posterDirected byDaniel MannWritten byJohn PatrickBased onThe Teahouse of the August Moon1951 novelby Vern J. SneiderProduced byJack CummingsStarringMarlon BrandoGlenn FordMachiko KyōEddie AlbertPaul FordHarry MorganCinematographyJohn AltonEdited byHarold F. KressMusic bySaul ChaplinJune HersheyKikuko KanaiDon SwanderKikuro KanaiProductioncompanyMetro-Goldwyn-MayerDistributed byLoew's Inc.Release date November 29...

Bruce Springsteen's backing band E Street BandBruce Springsteen and the E Street Band at the end of a performance in 2009Background informationOriginBelmar, New Jersey, U.S.Genres Rock rock and roll Years active 1972–1989 1995 1999–present LabelsColumbiaMembers Bruce Springsteen Garry Tallent Roy Bittan Max Weinberg Steven Van Zandt Nils Lofgren Patti Scialfa With:[1] Soozie Tyrell Charles Giordano Jake Clemons Past members Clarence Clemons Danny Federici Vini Lopez David Sancious...

Laws that allow, prohibit, or regulate abortion Legality of abortion by country or territory Legal on request: No gestational limit Gestational limit after the first 17 weeks Gestational limit in the first 17 weeks Unclear gestational limit Legally restricted to cases of: Risk to woman's life, to her health*, rape*, fetal impairment*, or socioeconomic factors Risk to woman's life, to her health*, rape, or fetal impairment Risk to woman's life, ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (novembre 2021). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Réseau de bus TisséoLignes de 13 à 87 Un Heuliez GX 327 et un Iveco Urbanway sur les lignes ...
Village in East Sussex, England Human settlement in EnglandDitchlingVillage main road (Lewes Road) with post office and general storeDitchlingLocation within East SussexArea15.49 km2 (5.98 sq mi) [1]Population2,081 (2011)[2]• Density339/sq mi (131/km2)OS grid referenceTQ325151• London50 miles (80 km) NDistrictLewesShire countyEast SussexRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townHasso...

Turboprop homebuilt aircraft type Epic LT & Dynasty Role Single engine turboprop light aircraftType of aircraft National origin United States Manufacturer Epic Aircraft First flight 2004[1] Status Production resumed in 2010[2] Produced 2004–2009; 2010[2]–2018[3] Number built 54[3] Variants CAIGA Primus 150Epic E1000 The Epic LT is an American kit-built single-engined turboprop aircraft intended for use by private pilots. The Epic Dynasty was the...

Looney Tunes: Due conigli nel mirinofilm d'animazione direct-to-video Lola e Bugs in una scena del film Titolo orig.Looney Tunes: Rabbits Run Lingua orig.inglese PaeseStati Uniti RegiaJeff Siergey Produttore esecutivoSam Register ProduttoreHugh Davidson, Jeff Siergey SoggettoHugh Davidson, Larry Dorf, Rachel Ramras SceneggiaturaHugh Davidson, Rachel Ramras Char. designKaukab Basheer, Mark Christiansen, Dan Haskett, Jennie Hoffer Dir. artisticaJo...

ザッツお台場エンターテイメント!(第1 - 7夜 ○○○の38年) 7日間全て生放送を行ったフジテレビ台場本社(FCGビル。写真は1996年完成当時のもの)ジャンル 特別番組出演者 各番組を参照製作プロデューサー 渡邉光男ほか制作 フジテレビ 放送音声形式ステレオ放送放送国・地域 日本放送期間1997年3月31日 - 4月6日放送時間19:00 - 21:24放送分各144分、7日間延べ1008分回数7テ�...

Historic county in ScotlandPeeblesshireHistoric countyCountryScotlandCounty townPeeblesArea • Total548 sq mi (1,419 km2) Ranked 16th of 34Chapman codePEE Peeblesshire (Scottish Gaelic: Siorrachd nam Pùballan), the County of Peebles or Tweeddale is a historic county of Scotland. Its county town is Peebles, and it borders Midlothian to the north, Selkirkshire to the east, Dumfriesshire to the south, and Lanarkshire to the west.[1] History The origins of...
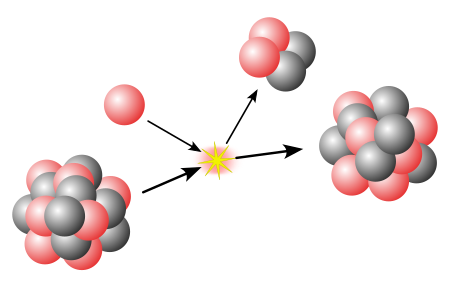
Series of radioactive decays Nuclear physics Nucleus Nucleons p n Nuclear matter Nuclear force Nuclear structure Nuclear reaction Models of the nucleus Liquid drop Nuclear shell model Interacting boson model Ab initio Nuclides' classification Isotopes – equal Z Isobars – equal A Isotones – equal N Isodiaphers – equal N − Z Isomers – equal all the above Mirror nuclei – Z ↔ N Stable Magic Even/odd Halo Borromean Nuclear stability Binding energy p–n ratio Drip li...

Cet article est une ébauche concernant une localité italienne et les Pouilles. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Palmariggi Administration Pays Italie Région Pouilles Province Lecce Code postal 73020 Code ISTAT 075058 Préfixe tel. 0836 Démographie Population 1 460 hab. (30-11-2018[1]) Densité 183 hab./km2 Géographie Coordonnées 40° 08′ 00″ nord...

2006 novel by Bruce R. Cordell The topic of this article may not meet Wikipedia's notability guideline for books. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Darkvision novel – news · newspapers · books ...