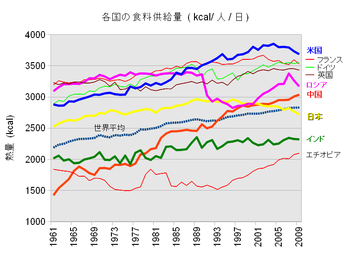
飢餓
| |||||||||||||||||||||||||||||||||||||||||
Read other articles:

Ōmuta 大牟田市Kota BenderaLambangLokasi Ōmuta di Fukuoka PrefectureNegara JepangWilayahKyūshūPrefektur FukuokaPemerintahan • WalikotaYoshitaka SekiLuas • Total81,5 km2 (315 sq mi)Populasi (Oktober 1, 2015) • Total117.360 • Kepadatan1.440/km2 (3,700/sq mi)Zona waktuUTC+9 (Waktu Standar Jepang)Simbol • PohonQuercus acutissima• BungaCamellia japonicaSitus webSitus web resmi Ōmuta (大牟田市cod...

Ermesinda dari Asturias, oleh Francisco Joaquín Gutiérrez de la Vega. 1854. (Museo del Prado, Madrid). Ermesinda (skt. 720 atau skt. 730 — ?) atau Ormisenda, Ermisenda, Ermesinde, Ermessenda) adalah permaisuri Kerajaan Asturias, sebagai istri Raja Alfonsu I dari Asturias (Alfonsu yang Katolik). Dia adalah putri Raja Pelayo dari Asturias dan ratunya, Gaudiosa. Chronicon Albeldense berbahasa Latin menyatakan bahwa Ermesinda adalah putri Pelagius, raja pertama Asturias, dan ratunya, Gau...

Berbagai jenis jarum rajut Orang sedang merajut memakai dua jarum rajut. Jarum rajut atau hakpen adalah alat yang dipakai sewaktu merajut benang dengan tangan untuk menghasilkan kain rajutan. Bentuknya yang paling umum berupa batang panjang yang meruncing pada salah satu ujungnya, tetapi tidak seruncing jarum jahit. Jarum jenis ini dipergunakan dalam merajut dengan teknik kniitting. Jarum untuk merenda yang memiliki pengait pada ujungnya disebut disebut jarum renda (hakpen). Jarum jenis ini d...

Karya seni kelas bayat, dari buku tahunan Locust tahun 1920 East Texas State Normal College Bayat, bayata (laki-laki), bayati (perempuan), atau bahasa sehari-hari mahasiswa baru, [1] adalah seseorang pada tahun pertama di suatu lembaga pendidikan, biasanya sekolah menengah atau di tingkat perguruan tinggi dan universitas, tetapi juga dalam bentuk lembaga pendidikan pasca sekolah menengah lainnya.[2] Referensi ^ Frosh Definition & Meaning. Merriam-Webster. Diakses tanggal A...
المنظمة الأوروبية لسلامة الملاحة الجوية المنظمة الأوروبية لسلامة الملاحة الجوية البلد بلجيكا هولندا لوكسمبورغ فرنسا المقر الرئيسي مدينة بروكسل تاريخ التأسيس 1960 الموازنة 505800000 يورو (2014) عدد الموظفين 1945 (2014)1894 (2016)[1] الموقع الرسمي الموقع ال...

Symbols representing numbers This article is not about the history of numbers, but rather about the history of numerals, i.e. symbols for representing numbers. See also History of the Hindu–Arabic numeral system. Part of a series onNumeral systems Place-value notation Hindu-Arabic numerals Western Arabic Eastern Arabic Bengali Devanagari Gujarati Gurmukhi Odia Sinhala Tamil Malayalam Telugu Kannada Dzongkha Tibetan Balinese Burmese Javanese Khmer Lao Mongolian Sundanese Thai East Asian syst...

Danish cyclist (1936–2013) Palle LykkePalle Lykke in 1956Personal informationBorn(1936-11-04)4 November 1936Ringe, DenmarkDied19 April 2013(2013-04-19) (aged 76)Antwerp, BelgiumTeam informationDisciplineTrack and road cyclingMajor winsOne-day races and Classics Kampioenschap van Vlaanderen (1954) Track Championships National Track Championships Sprint (1958, 1959, 1960, 1961) Medal record Representing Denmark UEC European Track Championships 1959 Madison 1962 Madison 1963 Derny 1...

Fyodor Vasilievich Rostopchin Fyodor Vasilievich Rostopchin (bahasa Rusia: Фёдор Васильевич Ростопчин) (3.12(23).1763 - 1.18(30).1826) adalah negarawan kontroversial Rusia. Ia tampil sebagai karakter dalam War and Peace. Fyodor Rostopchin memiliki pengaruh besar terhadap tsar Paul I. Referensi Artikel ini menyertakan teks dari suatu terbitan yang sekarang berada pada ranah publik: Chisholm, Hugh, ed. (1911). perlu nama artikel . Encyclopædia Britan...

Natasha St-PierInformasi latar belakangNama lahirNatasha St-PierLahir10 Februari 1981 (umur 43) New Brunswick, KanadaGenrePopPekerjaanPenyanyi, pencipta laguInstrumenVokal, pianoTahun aktif1996–sekarangLabelSony MusicSitus webwww.natasha-stpier.com Natasha St-Pier (lahir 10 Februari 1981) adalah seorang penyanyi berkebangsaan Kanada. Ia merilis album pertamanya pada tahun 1996 yang diberi judul Émergence. Namun, namanya baru melambung pada album keduanya yang berjudul À chacun son hi...

Canadian ice hockey player Ice hockey player Armand Mondou Born (1905-06-27)June 27, 1905Yamaska, Quebec, CanadaDied September 13, 1976(1976-09-13) (aged 71)Height 5 ft 10 in (178 cm)Weight 175 lb (79 kg; 12 st 7 lb)Position ForwardShot LeftPlayed for Montreal CanadiensPlaying career 1926–1940 Joseph Armand Mondou (June 27, 1905 - September 13, 1976) was a Canadian ice hockey forward. Mondou was born in Yamaska, Quebec. He played his entire Nation...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Maria LojaLahir12 Februari 1890Hamburg, Kekaisaran JermanMeninggal3 Januari 1953 (usia 62)Berlin Barat, Jerman BaratPekerjaanPemeranTahun aktif1934-1953 (film) Maria Loja (12 Februari 1890 – 3 Januari 1953) adalah seorang pemeran ...

Overview of emergency medical services in South Africa Paramedics loading a patient into an air ambulance after a train crash in Pretoria Emergency medical services in South Africa are a public/private system aimed at the provision of emergency ambulance service, including emergency care and transportation to hospital. Organization Land Ambulance Emergency ambulance service is provided by each South African province. The government-operated ambulance system, also known in the Western Cape as ...

Untuk kegunaan lain, lihat Aurora (disambiguasi). AuroraMunicipalityMap of Zamboanga del Sur showing the location of AuroraCountry PhilippinesRegionWestern Mindanao (Region IX)ProvinceZamboanga del SurDistrict1st District of Zamboanga del SurFoundedAugust 22, 1942Barangays44Pemerintahan • MayorEnrique J. CabahugLuas • Total117,48 km2 (4,536 sq mi)Populasi (2007) • Total47.177 • Kepadatan4,0/km2 (10/sq mi)Zona waktuU...

Questa pagina è un archivio di passate discussioni. Per favore non modificare il testo in questa pagina. Se desideri avviare una nuova discussione o riprenderne una precedente già archiviata, è necessario farlo nella pagina di discussione corrente. Archivio46 Archivio48 Archivio 04/07/06 - 01/09/06 29/08/06 - 25/09/06 03/10/06 - 30/11/06 08/12/06 - 02/02/07 04/02/07 - 31/03/07 31/03/07 - 30/09/07 02/10/07 - 02/04/08 02/04/08 - 24/07/08 29/07/08 - 29/10/08 31/10/08 - 17/11/08 20/11/08 - 16...
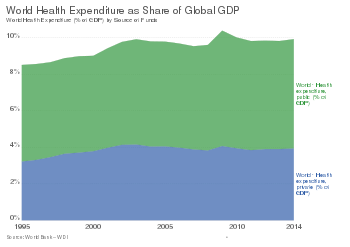
Branch of economics For the journal, see Health Economics. World health expenditure as share of global GDP.[1] How much did the UK spend on healthcare in 2012? Part of a series onPublic health Outline Subfields Community health Dental public health Environmental health Epidemiology Health economics Health education Health promotion Health policy Health politics Mental health Occupational safety Rehabilitation (penology) Sexual and reproductive health Sanitation World health (Global he...

حسان اگزار چنانی معلومات شخصية مكان الميلاد قرية الخويس من أعمال ناحية شاوور بیت رشگ/ مدينة الشوش تاريخ الوفاة سنة 2010 سبب الوفاة نوبة قلبية الجنسية أهواز، إيراني الاسم المستعار حسان اگزار – اگزار – فنان الربابة الحياة العملية المهنة موسيقي، ملحن، مغني عازف/مادح ا�...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (December 2014) (Learn how and when to remove this message) Part of a series on theCulture of Korea Society History People Diaspora Language Names of Korea Religion Arts and literature Architecture Art Pottery Painting Dance Film North South Literature North South Poetry Manhwa...

1914 battle of the First World War Battle of RossignolPart of Battle of the Frontiers of the First World WarThe village of Rossignol after the battleDate22 August 1914 (1914-08-22)LocationRossignol, near Tintigny, Belgium49°43′2″N 5°29′17″E / 49.71722°N 5.48806°E / 49.71722; 5.48806 (Le Centre Mémoriel de Rossignol)Result German victoryBelligerents France German EmpireCommanders and leaders Jules Lefèvre Kurt von Pritzel...

جمهورية العراق وزارة الكهرباء وزارة الكهرباء (العراق) تفاصيل الوكالة الحكومية البلد العراق تأسست 2003 المركز بغداد، العراق هيئة الكهرباء الإدارة منصب المدير وزير الكهرباء [لغات أخرى] الوزراء المسؤولون زياد علي فاضل، (وزير) موقع الويب الموقع الرسمي ت�...

L'algebra di Boole (anche detta algebra booleana, logica booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0. Indice 1 Storia 2 Descrizione 3 Definizione formale 3.1 Legge di dualità 3.2 Complementi di 0 e 1 3.3 Convoluzione 3.4 Elementi neutri 3.5 Assorbimento del complemento (secondo teorema dell'assorbimento) 3...