強いCP問題
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Danielle Lloyd – berita · surat kabar · buku · cendekiawan · JSTOR (September 2021) Danielle O'HaraLahirDanielle Lloyd16 Desember 1983 (umur 40)LiverpoolSuami/istriJamie O'Hara (m. 2012 c. 2014)Michael O...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Lafadl adalah sebuah lembaga kajian dan publikasi yang didirikan oleh sekelompok anak muda di Yogyakarta yang punya perhatian khusus pada persoalan masyarakat Dunia Ketiga. Lafadl berdiri pada tanggal 21 Agustus 2000. Lafadl percaya bahwa another world i...

Festival Film Indonesia ke-26Tanggal2 Desember 2006 (Piala Vidia)21 Desember 2006 (Piala Citra)TempatBalai Sarbini, Setiabudi, Jakarta Selatan (Piala Vidia)Plenary Hall Jakarta Convention Center, Senayan, Jakarta Pusat (Piala Citra)Pembawa acara Ferdi Hasan Sarah Sechan PenyelenggaraBadan Pertimbangan Perfilman NasionalSorotanFilm TerbaikEkskul (Dibatalkan)[1][2]Seri Drama TerbaikTante TutiPenyutradaraan TerbaikNayato Fio Nuala (Dibatalkan)[3]EkskulAktor TerbaikAlbert ...
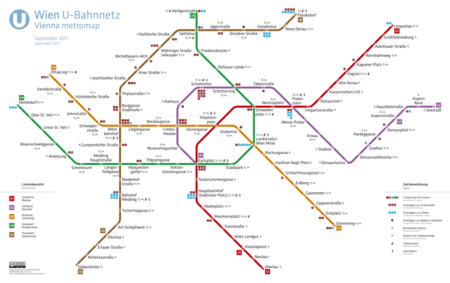
U-Bahn WienJaringan U-Bahn WinaInfoWilayahWinaJenisAngkutan cepatJumlah jalur5Jumlah stasiun90Penumpang harian1.300.000Situs webwww.wienerlinien.atOperasiDimulai1978OperatorWiener LinienTeknisPanjang sistem74,6 km (46,4 mi)Lebar sepur1.435 mm (4 ft 8+1⁄2 in)Listrik750 V DC Rel ketiga dan kabel melayang U-Bahn Wina (kependekan dari Untergrundbahn, atau kereta api bawah tanah) adalah sebuah sistem angkutan cepat (metro) yang terdiri dari lima jalur. Jalur ini...

Une onde mécanique progressive est le phénomène de propagation d'une perturbation locale dans un milieu matériel[1]. Si elle est de plus périodique, la caractéristique principale de l'onde progressive est que la perturbation se retrouve identique à elle-même après une durée T (période temporelle de propagation) et à une distance de lambda (période spatiale de propagation ou longueur d'onde). Il faut pour cela que le milieu de propagation ait une extension infinie ou, tout du moin...

Peter Gomez al Festival Internazionale del Giornalismo nel 2015 Peter Gomez Homen (New York, 23 ottobre 1963) è un giornalista, saggista, conduttore televisivo, autore televisivo, opinionista e blogger statunitense naturalizzato italiano[1], fondatore e dal 23 settembre 2009 direttore della versione online de il Fatto Quotidiano. Indice 1 Biografia 2 Vita privata 3 Curiosità 4 Pubblicazioni 5 Televisione 6 Filmografia 7 Note 8 Voci correlate 9 Altri progetti 10 Collegamenti esterni ...

Ini adalah nama Melayu; nama Yusof merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Redzuan. Kata bin (b.) atau binti (bt.), jika digunakan, berarti putra dari atau putri dari. Yang Berbahagia Datuk SeriMohd Redzuan Md YusofDGSMمحمد رضوان مد يوسف Menteri di Sekretariat Perdana Menteri Malaysia (Bidang Penugasan Khusus)Masa jabatan10 Maret 2020 – 16 Agustus 2021Perdana MenteriMuhyiddin YassinWakilMastura Mohd YazidPendahulu...

Pokémon Go Publikasi 6 Juli 2016 AUS: 6 Juli 2016 NA: 6 Juli 2016[note 1] EU: 13 Juli 2016[note 1] JP: 22 Juli 2016 VersiDaftarAndroid: 0.277.2 (17 Juli 2023)iOS: 0.277.2 (17 Juli 2023) GenreRealitas tertambahModel bisnisFree-to-play dan in-app purchases Bahasa Daftar Inggris, Italia, Jepang, Jerman, Prancis, Spanyol dan Tionghoa 60 Karakteristik teknisSistem operasiAndroid dan iOS PlatformAndroid, iOS dan iPadOS MesinUnityModePermainan video pemain tunggal dan permainan vide...

Voce principale: L.R. Vicenza Virtus. Vicenza CalcioStagione 2005-2006Sport calcio Squadra Vicenza Allenatore Giancarlo Camolese Presidente Sergio Cassingena Serie B16º posto Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Vitiello (38)Totale: Vitiello (39) Miglior marcatoreCampionato: González e Schwoch (8)Totale: Schwoch (9) StadioStadio Romeo Menti 2004-2005 2006-2007 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Vicenza Calcio nel...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Supriyanto GSPrie GS pada tahun 2019LahirSupriyanto(1965-02-03)3 Februari 1965Kendal, Jawa Tengah, IndonesiaMeninggal12 Februari 2021(2021-02-12) (umur 57)Semarang, Jawa Tengah, IndonesiaSebab meninggalSerangan jantungAlmamaterIKIP Semarang (kini Universitas Negeri Semarang)OrganisasiSuara Merdeka Supriyanto (3 Februari 1965 – 12 Februari 2021) atau yang lebih dikenal sebagai Prie GS adalah budayawan berkebangsaan Indonesia. Dia mengawali kariernya sebagai wartawan ...

Swedish football midfielder (born 1997) Nathalie Persson Personal informationFull name Anna Nathalie Hoff PerssonDate of birth (1997-04-18) 18 April 1997 (age 27)Place of birth SwedenPosition(s) MidfielderTeam informationCurrent team Malmö FFNumber 2Youth career IF Limhamn Bunkeflo FC RosengårdSenior career*Years Team Apps (Gls)2014–2015 FC Rosengård 31 (3)2016–2018 Kopparbergs/Göteborg FC 47 (1)2018 Sporting CP 2019 IF Limhamn Bunkeflo 21 (2)2020–2023 KIF Örebro 85 (0)2024–...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...
Warsaw metro station Plac WilsonaGeneral informationCoordinates52°16′9″N 20°59′3″E / 52.26917°N 20.98417°E / 52.26917; 20.98417Owned byPublic Transport AuthorityPlatforms1 island platformTracks2Connections 114, 116, 122, 157, 181, 185, 303, 518 N44, N46 6, 15, 36ConstructionStructure typeUndergroundPlatform levels1AccessibleYesOther informationStation codeA-18Fare zone1HistoryOpened8 April 2005; 19 years ago (2005-04-08)Services Preceding ...

Presidential library of Donald Trump, 45th President of the United States Donald J. Trump Presidential LibraryAvailable inEnglishHeadquartersTo be announcedCountry of originUnited StatesOwnerNational Archives and Records AdministrationCreated byArchival Operations Division – Trump Presidential LibraryKey peopleDonald TrumpURLtrumplibrary.govCommercialNoLaunchedJanuary 20, 2021; 3 years ago (2021-01-20)Content licensePublic domain This article is part of a se...

County-level city in Yunnan, ChinaMangshi 芒市County-level cityOther transcription(s) • PinyinMángshì • Tai Nueaᥝᥥᥒᥰ ᥛᥫᥒᥰ ᥑᥩᥢᥴ • JingphoMangshi Myu • Burmeseမန်စီ • Thaiเมืองข้อนClockwise: Urban skyline, Menghuan Pagoda, Mangshi Little Hall, Mangshi Square, Puti TempleEtymology: Evolved form the ethnic name 茫施 (Mangshi)Nickname: city of dawnTerritory of Mangshi (r...

Invasion of southern Lebanon by Israel as part of the Lebanese Civil War Not to be confused with the South Lebanon conflict (1985–2000). 1978 South Lebanon conflictPart of the Palestinian insurgency in South Lebanon and the Israeli–Lebanese conflictIsraeli soldiers meeting with Lebanese ex-military officer Saad Haddad during the invasionDate14–21 March 1978LocationSouth Governorate and Nabatieh GovernorateResult Israeli victoryTerritorialchanges Palestinian withdrawal from South Lebanon...

Disambiguazione – Rosmini rimanda qui. Se stai cercando altri significati, vedi Rosmini (disambigua). Beato Antonio RosminiAntonio Rosmini ritratto da Francesco Hayez, 1853-1856 Presbitero NascitaRovereto, 24 marzo 1797 MorteStresa, 1º luglio 1855 (58 anni) Venerato daChiesa cattolica Beatificazione18 novembre 2007 da papa Benedetto XVI Ricorrenza1º luglio Manuale Antonio Francesco Davide Ambrogio Rosmini Serbati (Rovereto, 24 marzo 1797 – Stresa, 1º luglio 185...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2019) تيموثي ديفيس (بالإنجليزية: Timothy Davis) معلومات شخصية الميلاد 29 مارس 1794 نيوآرك الوفاة 27 أبريل 1872 (78 سنة) القادر مواطنة الولايات المتحدة ا�...

Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện bài viết này bằng cách bổ sung chú thích tới các nguồn đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ. Âm nhạc Kitô giáo là các thể loại nhạc diễn tả niềm tin cá nhân hoặc cộng đoàn trong cuộc sống và đức tin Kitô giáo (Cơ Đốc giáo), được hình thành để phục vụ...













![{\displaystyle Z=\int {\mathcal {D}}A\,{\mathcal {D}}\psi \,{\mathcal {D}}{\bar {\psi }}\,\exp i\int d^{4}x\left[i{\bar {\psi }}D_{\mu }\gamma ^{\mu }\psi -{\frac {1}{4}}F^{a\mu \nu }F_{\mu \nu }^{a}-{\frac {g^{2}\theta }{32\pi ^{2}}}{\tilde {F}}^{a\mu \nu }F_{\mu \nu }^{a}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9889696f8dfd82eabfee8ed5cf711f63ed8fa6c)

![{\displaystyle {\mathcal {D}}\psi \,{\mathcal {D}}{\bar {\psi }}\mapsto \exp \left[-i\int d^{4}x{\frac {g^{2}\alpha }{16\pi ^{2}}}{\tilde {F}}^{\mu \nu }F_{\mu \nu }\right]{\mathcal {D}}\psi \,{\mathcal {D}}{\bar {\psi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b7cc078aa5afed3c694223ff97b23629a17c8d)











