CR多様体
|
Read other articles:

Québec Québec (bahasa Prancis)Province BenderaLambang kebesaranMotto: Je me souviens(terjemahan: Saya ingat) BC AB SK MB ON QC NB PE NS NL YT NT NU NegaraKanadabergabung dengan konfederasi1 Juli 1867 (urutan ke-ke-1, bersama Ontario, Nova Scotia, New Brunswick)Ibu kotaKota QuebecKota terbesarMontreal Metro terbesarMontreal Raya Pemerintahan • Letnan GubernurJ. Michel Doyon • Perdana MenteriFrançois Legault (CAQ) DPRDMajelis Nasional QuebecJumlah Perwakilandi Pa...

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (January 2024) (Learn how and when to remove this template message)States and union territories of India ordered by Area Population GDP (per capita) Abbreviations Access to safe drinking water Availability of toilets Capitals Child nutrition Crime rate Ease of doing business Electricity penetration Export...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

American boxer and actor (1907–1976) Maxie RosenbloomRosenbloom in 1941BornMax Everitt Rosenbloom(1906-11-06)November 6, 1906[2]Leonard Bridge, Connecticut, U.S.DiedMarch 6, 1976(1976-03-06) (aged 69)South Pasadena, California, U.S.Other namesSlapsy MaxieStatisticsWeight(s) Middleweight Light heavyweight Heavyweight StanceOrthodox Boxing recordTotal fights298;[1] with the inclusion of newspaper decisionsWins223Wins by KO19Losses44Draws29No contests2 Max Everitt Ros...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Serie D 1979-1980 Competizione Serie D Sport Calcio Edizione 21ª Organizzatore Lega Semiprofessionisti Luogo Italia Partecipanti 108 Formula 6 gironi all'italiana Risultati Prom...

California-based reality television series in the United States Laguna Beach: The Real Orange CountyGenreReality televisionCreated byLiz GateleyStarring Lauren Conrad Kristin Cavallari Stephen Colletti Trey Phillips Christina Schuller Morgan Olsen Talan Torriero Lo Bosworth Jessica Smith Alex Murrel Jason Wahler Taylor Cole Tessa Keller Chase Johnson Raquel Donatelli Cameron Brinkman Kyndra Mayo Lexie Contursi Cami Edwards Kelan Hurley Breanna Conrad Narrated by Lauren Conrad Kristin Cavallar...

La costa Noroeste durante la época del comercio marítimo de pieles, de 1790 a 1840 Se conoce como comercio marítimo de pieles al comercio de pieles marinas capturadas en la costa del Pacífico Noroeste desde mediados del siglo XVIII hasta mediados del siglo XIX, que eran transportadas por barco a China, donde se vendían o intercambiaban por otras mercancías. Se centraba en la adquisición de pieles de nutria marina y otros animales a los pueblos indígenas de la costa del Pací...
Hillary Janssens Nazionalità Canada Canottaggio Specialità 2 senza, 4 senza, Otto Squadra UBC Thunderbirds Vancouver CarrieraNazionale CanadaPalmarès Competizione Ori Argenti Bronzi Giochi olimpici 0 0 1 Mondiali 1 1 1 Mondiali U23 1 1 1 Per maggiori dettagli vedi qui Statistiche aggiornate al 13 settembre 2023 Modifica dati su Wikidata · Manuale Hillary Janssens (Surrey, 21 luglio 1994) è una canottiera canadese, campionessa olimpica nell'otto a Tokyo 2020.[1] In...

† Стеллерова корова Муляж стеллеровой коровы в Лондонском музее естествознания Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстно�...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

اضغط هنا للاطلاع على كيفية قراءة التصنيف عظايا مامنتشي حالة الحفظ أنواع منقرضة المرتبة التصنيفية فصيلة التصنيف العلمي النطاق: حقيقيات النوى المملكة: حيوانات الشعبة: الحبليات الشعيبة: الفقاريات غير مصنف: الفكيات غير مصنف: رباعيات الأطراف غير مصنف: شبيهات الزواحف غي...

« Mythique » redirige ici. Pour les articles homophones, voir Meetic et Mythic. Pour l’article ayant un titre homophone, voir Mite. Pour un article plus général, voir Mythologie. Un mythe est une construction imaginaire qui se veut explicative des phénomènes cosmiques, psychologiques et sociaux, à l'image de dieux et déesses qui proposent une explication pour certains aspects fondamentaux du monde, et de la société qui l'a forgée ou qui la véhicule. Le mythe est port�...

Evasive maneuver vehicle test The evasive manoeuvre test (Swedish: Undanmanöverprov; colloquial: moose test or elk test; Swedish: Älgtest, German: Elchtest) is performed to determine how well a certain vehicle evades a suddenly appearing obstacle. This test has been standardized in ISO 3888-2.[1] Forms of the test have been performed in Sweden since the 1970s.[2] The colloquial and internationally better-known name for the test was coined in 1997 by the German newspaper Süd...

William RoweLahir26 Juli 1931 (umur 92)EraFilsafat kontemporerKawasanFilsafat BaratAliranFilsafat analitisMinat utamaFilsafat agama William Leonard Rowe (lahir 26 Juli 1931)[1] adalah seorang professor emeritus di Purdue University. Ia merupakan ahli dalam filsafat agama. Karyanya memainkan peran penting dalam kebangkitan filsafat analitis agama sejak tahun 1970-an.[2] Ia terkenal akan evidential argument from evil.[3] Karya The Problem of Evil and Some Vari...

Tactile form of the Latin script This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (June 2022) (Learn how and when to remove this message) A sample of decapoint. The relative efficiency of braille can be seen, as the line at the bottom is the braille transcription for the first two lines of decapoint: je vous prie de commander ...

Municipality in Mexico State, MexicoZumpahuacánMunicipalityTemple de San MateoCountryMexicoStateMexico StateMunicipal seatZumpahuacánTime zoneUTC-6 (CST) • Summer (DST)UTC-5 (CDT) Zumpuhuacán is a municipality in the State of Mexico. Its municipal seat is also called Zumpahuacán: The area was settled by Mexicas in 1220. Geography It is located between the parallels 99° 27’ 51” and 99° 37’ 32” west longitude, and 18° 41’ 35” and 18° 55’ 22” north latitu...

Colin Hanks al South by Southwest 2015 Colin Lewes Hanks (Sacramento, 24 novembre 1977) è un attore statunitense. Indice 1 Biografia 1.1 Carriera 1.2 Vita privata 2 Filmografia 2.1 Cinema 2.2 Televisione 3 Doppiaggio 4 Doppiatori italiani 5 Altri progetti 6 Collegamenti esterni Biografia Nato dal primo matrimonio dell'attore Tom Hanks (finito con un divorzio quando aveva 10 anni) con l'attrice Samantha Lewes, morta per un cancro alle ossa nel 2002, ha una sorella, Elizabeth (nata nel 1982), ...

Questa voce sull'argomento programmi televisivi italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Rai dire NiùsLogo di Rai dire NiùsPaeseItalia Anno2017 Generetelegiornale satirico Edizioni1 Durata15 min Lingua originaleitaliano RealizzazioneConduttoreGialappa's Band, Mago Forest e Mia Ceran Rete televisivaRai 2 Modifica dati su Wikidata · Manuale Rai dire Niùs è stato un programm...
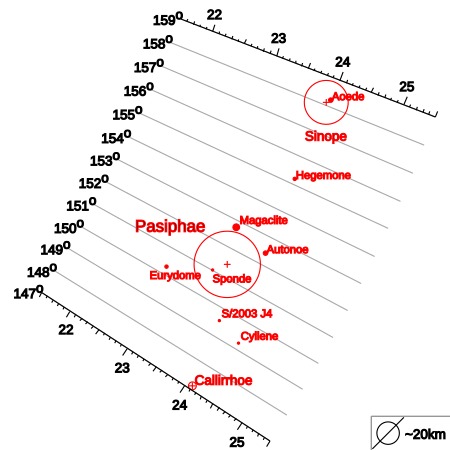
مجموعة باسيفي هي مجموعة مكونة من أقمار جميعها أقمار غير نظامية وتتحرك بحركة تراجعية دائرة حول المشتري على مسافة تتراوح بين 22.8 و 24.1 جيجامتر وزاوية ميلان تتراوح تقريباً بين 144.5° و 158.3°. تضم هذه المجموعة الأقمار التالية مرتبة من الأكبر إلى الأصغر:[1] باسيفي سينوبي , ثلثي حجم...







![{\displaystyle [L,L]\subset L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b278eb6ad9c56353acd6494fc3d66edc3ace1cce)








![{\displaystyle h(v,w):={\frac {1}{2i}}[v,{\bar {w}}]\mod L\oplus {\bar {L}},\quad v,w\in L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48cf330c748e8ae113c1aa3d738c4a781cd4b6a2)




![{\displaystyle h_{\alpha }(v,w)=d\alpha (v,{\bar {w}})=-\alpha ([v,{\bar {w}}]),\quad v,w\in L\oplus {\bar {L}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03cd1e78ec7138f039f73733bb1a96a123d97410)

















![{\displaystyle [L_{j},{\overline {L}}_{j}]=-2iT.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67bbad8fa4495732b69602cb3785f8001e5d6a5d)




