鈴木重禮
|
Read other articles:

Dalam aljabar abstrak, homomorfisme atau kehomomorfan (Inggris: Homomorphismcode: en is deprecated ) adalah struktur peta yang menghubungkan dua struktur aljabar. Setiap homomorfisme pasti dapat ditentukan kanelnya, dan kanel pasti subgrup normal, sehingga selalu dapat dibentuk grup faktor, selanjutnya akan dibentuk pengkaitan baru dari ranah homomorfisme ke grup faktor yang dibentuknya, sehingga terbentuklah homomorfisme baru yang disebut homomorfisma natural. Definisi Homomorfisme adalah pe...

Untuk sinetron SCTV, lihat Anak Sekolahan. Anak SekolahPoster resmiGenreKomediPemeranDenny CagurRina NoseVicky PrasetyoVicky NitinegoroDede SunandarArafah RiantiAci RestiAmanda RigbyAbdel AchrianOpie KumisChika JessicaLagu pembukaAnak SekolahLagu penutupAnak SekolahNegara asalIndonesiaBahasa asliBahasa IndonesiaBahasa SundaProduksiProduserYustina PramitaDurasi60 menit (Kamis-Jumat)Rumah produksiTrans7DistributorTrans MediaRilis asliJaringanTrans7Format gambarDolby Digital HD 16:9Format audioS...

Measure protecting bank depositors from losses caused by a bank default This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: the article contains multiple external links embedded in the body text. These need to be removed or converted to references. Please help improve this article if you can. (Dec...

Species of fungus Taphrina wiesneri Scientific classification Domain: Eukaryota Kingdom: Fungi Division: Ascomycota Class: Taphrinomycetes Order: Taphrinales Family: Taphrinaceae Genus: Taphrina Species: T. wiesneri Binomial name Taphrina wiesneri(Rathay) Mix Taphrina wiesneri is a plant pathogen causing witch's broom, or plant gall formations, on cherry trees (Prunus & Cerasus spp). It is an important pest species of the ornamental cherry Cerasus X yedoensis in Japan.[1] Lif...

Olivier Jenot Contexte général Sport Ski alpin Période active 2003-2018 Biographie Nationalité sportive Monaco Nationalité Monaco Naissance 28 février 1988 (36 ans) Lieu de naissance Monaco Taille 1,75 m (5′ 9″) Poids de forme 75 kg (165 lb) Club Monte Carlo ski club modifier Olivier Jenot, né le 28 février 1988 à Monaco, est un skieur alpin monégasque. Biographie Il prend part à ses premières courses FIS lors de l'hiver 2003-2004. Il entre dans...

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

American prelate of the Roman Catholic Church This article is about the cardinal. For the American football player, see Roger Mahoney (American football). His EminenceRoger Michael MahonyKGCHSCardinalArchbishop Emeritus of Los AngelesMahony in March 2006ArchdioceseArchdiocese of Los AngelesAppointedJuly 12, 1985InstalledSeptember 5, 1985RetiredMarch 1, 2011PredecessorTimothy ManningSuccessorJosé Horacio GómezOther post(s)Cardinal-Priest of Ss. Quattro CoronatiOrdersOrdinationMay 1, 1962by&#...

Guido de' RossiStemma dei Rossi di San SecondoNascitaSan Secondo Parmense, 1440 circa MorteVenezia, 1490 Dati militariPaese servito Ducato di Milano Repubblica di Venezia CampagneBattaglia contro il ducato di Milano voci di militari presenti su Wikipedia Manuale Guido de' Rossi (San Secondo Parmense, circa 1440 – Venezia, 1490) è stato un condottiero italiano, erede designato di Pier Maria II de' Rossi Conte di San Secondo. Indice 1 Biografia 2 Discendenza 3 Curiosità 4 ...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Glanford Park di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemah...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2019) (Learn how and when to remove this template message) Hyundai Sonata police car in Gimhae, South Korea. South Korean and North Korean authorities at the South Korea-North Korea border. South Korea has a relatively unified and integrated approach to law enforcement. For example, the National Police...

NérignaccomuneLocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Vienne ArrondissementMontmorillon CantoneLussac-les-Châteaux TerritorioCoordinate46°18′N 0°44′E / 46.3°N 0.733333°E46.3; 0.733333 (Nérignac)Coordinate: 46°18′N 0°44′E / 46.3°N 0.733333°E46.3; 0.733333 (Nérignac) Superficie4,42 km² Abitanti145[1] (2009) Densità32,81 ab./km² Altre informazioniCod. postale86150 Fuso orarioUTC+1 Codic...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Сили спеціальних операцій Збройних сил України УкраїнаНомінал 10 гривеньМаса 12,4 гДіаметр 30 ммГурт рифленийМетал сплав на основі цинкуРоки карбування 2022Аверс Реверс У Вікіпедії є статті про інші значення цього терміна: Сили спеціальних операцій Збройних сил Укр...

Henry CapehartHenry CapehartLahir(1825-03-18)18 Maret 1825Johnstown, PennsylvaniaMeninggal15 April 1895(1895-04-15) (umur 70)Fargo, Dakota UtaraTempat pemakamanArlington National CemeteryPengabdianAmerika SerikatUnionDinas/cabangUnited States ArmyUnion ArmyLama dinas1861 – 1865Pangkat Lolonel Brevet Mayor JenderalKomandan 1st Regiment West Virginia Volunteer CavalryPerang/pertempuranPerang Saudara AmerikaPenghargaanMedal of Honor Henry Capehart (18 Maret 1825 – 15 ...

Pencak silat padaPekan Olahraga Nasional XIX Seni Putra Putri Tunggal Tunggal Ganda Ganda Regu Regu Tanding Putra Putri Kelas A Kelas A Kelas B Kelas B Kelas C Kelas C Kelas D Kelas D Kelas E Kelas E Kelas F Kelas F Kelas G Kelas H Kelas I Pencak silat kelas F putri pada Pekan Olahraga Nasional XIX dilaksanakan pada tanggal 20 sampai 24 september 2016 di Graha Laga Satria, ITB Jatinangor,Kabupaten Sumedang, Jawa Barat.[...

Airport in Angleton, TexasTexas Gulf Coast Regional AirportIATA: LJNICAO: KLBXFAA LID: LBXSummaryAirport typePublicOwnerBrazoria CountyServesAngleton / Lake Jackson, TexasLocation0 County Road 220, Angleton, Texas 77515Elevation AMSL25 ft / 8 mCoordinates29°06′31″N 095°27′44″W / 29.10861°N 95.46222°W / 29.10861; -95.46222Websitewww.flylbx.orgMapLBXLocation of airport in Texas / United StatesShow map of TexasLBXLBX (the United States)Show map ...

افتتاحية سوناتا للبيانو تصنيف كوشيل رقم 545 لموتسارت المصاحبة أو المُسايرة[1] (بالإنجليزية: Accompaniment) في الموسيقى هي الجزء أو الأجزاء المساعدة في عمل موسيقي. اللفظ يستخدم بشكل معتاد ليشير إلى مراجع الرسيتال الغنائي حيث يقدم آلة مفاتيح اللحن المصاحب، للسوناتات لآلة صولو ...
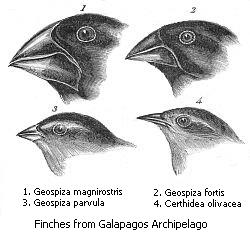
De vier vormen van soortvorming: Allopatrische soortvorming, peripatrische soortvorming, parapatrische soortvorming en sympatrische soortvorming. Soortvorming of speciatie is het ontstaan van nieuwe (biologische) soorten uit populaties van bestaande soorten. Het is een van de belangrijkste onderzoekgebieden binnen de evolutiebiologie. Charles Darwin plaatste in 1859 het soortvormingsproces in het centrum van zijn theorie en daarom is de titel van zijn belangrijkste werk De oorsprong der soort...

Axioms for the natural numbers In mathematical logic, the Peano axioms (/piˈɑːnoʊ/,[1] [peˈaːno]), also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th-century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete. The axiomatiza...
