入射層
|
Read other articles:

أوندريخ سيلوستكا معلومات شخصية الاسم الكامل أوندريخ سيلوستكا الميلاد 18 يونيو 1989 (العمر 34 سنة)زلين الطول 1.86 م (6 قدم 1 بوصة) مركز اللعب مدافع الجنسية جمهورية التشيك اللقب سيلوستكا الوزن 80 كغم معلومات النادي النادي الحالي سبارتا براغ الرقم 3 مسيرة الشباب سنوات فريق...

الهجوم الليلى على ترجوفيشت جزء من الحروب العثمانية الأفلاقية لوحة عن المعركة من قبل الرسام الروماني ثيودور أمان معلومات عامة التاريخ 17 يونيو، 1462 الموقع طريق نيكوبول وثم مدينة ترجوفيشت النتيجة كلا الطرفين إدعى النصر تغييراتحدودية إنسحاب العثمانيين وإكتفائهم بالغنائم ال...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Maesaan, Minahasa Selatan – berita · surat kabar · buku · cendekiawan · JSTOR MaesaanKecamatanPeta lokasi Kecamatan MaesaanNegara IndonesiaProvinsiSulawesi UtaraKabupatenMinahasa SelatanKode Kemenda...
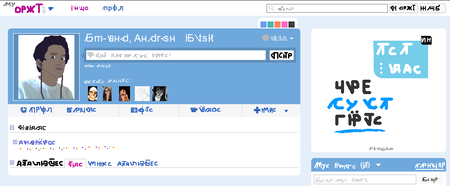
Orkut Logo d'Orkut Création 22 janvier 2004 Disparition 30 septembre 2014 Fondateurs Orkut Büyükkökten Slogan Who do you know? Direction Orkut Büyükkökten Actionnaires Google Activité Réseautage social Société mère Google Site web orkut.google.com/ modifier - modifier le code - voir Wikidata Aspect visuel du Nouvel Orkut. Texte factice. Orkut était un site de réseautage social qui permettait de mettre en relation les amis de ses amis (créer/gérer son réseau social). Il...

Public secondary school in Towson, Maryland, United StatesTowson High SchoolTowson Law & Public Policy High SchoolLocationTowson, MarylandUnited StatesCoordinates39°23′27″N 76°36′01″W / 39.39083°N 76.60028°W / 39.39083; -76.60028InformationTypePublic SecondaryMottoA Tradition of ExcellenceEstablished1873School districtBaltimore County Public SchoolsSuperintendentDarryl L. WilliamsPrincipalKimberly CulbertsonGrades9-12Enrollment1,442 (2008)[1]Ca...

Untuk kegunaan lain, lihat Philadelphia. Kota PhiladelphiaGabungan kota-countyDari kiri atas, panorama Philadelphia, patung Benjamin Franklin, Liberty Bell, Museum Seni Philadelphia, Balaikota Philadelphia, dan Independence Hall BenderaLambangJulukan: ZOMBIE CITY, Drunken City, Philly, City of Brotherly Love, The City that Loves you Back, Cradle of Liberty, The Quaker City, The Birthplace of America, The City of Neighborhoods(Philly, Kota Kasih Persaudaraan, Kota yang Mengasihi Anda Kemb...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

American sporting goods retailer Rock/CreekCompany typePrivateIndustryRetail, outdoor industryFounded1987HeadquartersChattanooga, TennesseeKey peopleDawson Wheeler and Marvin Webb, co-foundersJonathan Scott, vice presidentProductsClothing and outdoor equipmentNumber of employees50-99WebsiteRock/Creek Rock/Creek is a Chattanooga, Tennessee-based sporting goods retailer of clothing and gear for rock climbing, paddling, trail running, hiking, camping and travel. History Founded as Rock/Creek Out...

Species of flowering plant Terminalia chebula A leafless T. chebula tree Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Myrtales Family: Combretaceae Genus: Terminalia Species: T. chebula Binomial name Terminalia chebulaRetz. Synonyms[1][2] Buceras chebula (Retz.) Lyons Combretum argyrophyllum K.Schum. Myrobalanus chebula (Retz.) Gaertn. Myrobalanus gangetica (Roxb.) Kostel. Myrobalanus tomentella Ku...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

615 Karet Kuningan Halte TransjakartaHalte Karet Kuningan, 2023LetakKotaJakarta SelatanDesa/kelurahanKaret Kuningan, SetiabudiKodepos12940AlamatJalan HR Rasuna SaidKoordinat6°13′02″S 106°49′51″E / 6.21729°S 106.8309°E / -6.21729; 106.8309Koordinat: 6°13′02″S 106°49′51″E / 6.21729°S 106.8309°E / -6.21729; 106.8309Desain HalteStruktur BRT, median jalan bebas 1 tengah Pintu masukJembatan penyeberangan di sudut Jalan HR...

أرنولد بيكمان (بالإنجليزية: Arnold Orville Beckman) معلومات شخصية الميلاد 10 أبريل 1900(1900-04-10)[1]كولوم، إلينوي، الولايات المتحدة الأمريكية الوفاة 18 مايو 2004 (104 سنة) [1]لاهويا، كاليفورنيا، الولايات المتحدة الأمريكية الجنسية الولايات المتحدة الأمريكية عضو في الأكاديمية الأم�...

Typographical symbol or glyph (*) * redirects here. For other uses, see Asterisk (disambiguation) and * (disambiguation). For the comic book series, see Asterix. *AsteriskIn UnicodeU+002A * ASTERISK (*, *)RelatedSee alsoU+203B ※ REFERENCE MARK (komejirushi) U+A673 ꙳ SLAVONIC ASTERISK Look up * or asterisk in Wiktionary, the free dictionary. The asterisk (/ˈæstərɪsk/ *), from Late Latin asteriscus, from Ancient Greek ἀστε�...

2004 Indian general election ← 1999 20 April, 26 April, 5 and 10 May 2004 2009 → ← outgoing memberselected members →543 of the 545 seats in the Lok Sabha272 seats needed for a majorityRegistered671,487,930Turnout58.07% ( 1.92pp) First party Second party Third party Leader Sonia Gandhi Atal Bihari Vajpayee Harkishan Singh Surjeet Party INC BJP CPI(M) Alliance INC+ NDA LF Last election 28.30%, 114 seats 23.75%, 182 seats 5.40%, 33 ...

Renang pada Olimpiade Musim Panas 1952LokasiStadion Renang HelsinkiHelsinkiTanggal26 Juli–2 Agustus 1952Jumlah disiplin11Peserta319 dari 48 negara← 19481956 → Renang pada Olimpiade Musim Panas 1952 adalah pelaksanaan cabang olahraga renang pada penyelenggaraan Olimpiade Musim Panas 1952. Kompetisi pada cabang olahraga ini berlangsung di Stadion Renang Helsinki, Helsinki. Edisi ini menandingkan 11 nomor. 319 atlet dari 48 negara bertanding dalam edisi ini...

1's Album hit terbaik karya Destiny's ChildDirilis25 Oktober 2005 (2005-10-25)[1]Direkam1997–2005GenreR&B, hip-hopDurasi60:28 (versi standar)65:04 (versi asia)LabelColumbia RecordsProduserBeyoncé Knowles, Kelly Rowland, Michelle Williams (produser eksekutif), Mark J. Feist, Wyclef Jean, Cory Rooney, Rob Fusari, Kevin She'kspere Briggs, Swizz Beatz, Rodney Jerkins, 9th Wonder, Rich Harrison, David Foster, Ricky Ric Rude LewisKronologi Destiny's Child Destiny Fulfilled(...

Dutch day of remembrance of war dead This article is about the Dutch day of remembrance of war-dead. For other uses, see Death customs. Remembrance of the DeadCommemoration ceremony at Dam Square in Amsterdam on 4 May 2014Official nameDodenherdenkingObserved byNetherlandsTypeRemembranceSignificanceCommemorates all war casualties since the beginning of WWIIObservancesTwo-minute silenceDate4 MayNext time4 May 2025 (2025-05-04)FrequencyAnnualRelated toLiberation Day Remembran...

Artikel ini bukan mengenai PSX. Halaman ini berisi artikel tentang konsol rumahan pertama diproduksi oleh Sony. Untuk merek PlayStation pada umumnya, lihat PlayStation. PlayStationAtas: Model asli (1994) dengan PlayStation Pengendali dan Kartu memoriDasar: PS One (2000) yang lebih kecil dan didesain ulang dengan DualShock Pengendali dan Kartu MemoriPengembangSony Computer EntertainmentPembuatSony ElectronicsKeluarga produkPlayStationJenisKonsol permainan video rumahGenerasiKelimaTanggal rili...

Pour un article plus général, voir Élections régionales françaises de 2015. 2010 2021 Élections régionales de 2015 en Aquitaine-Limousin-Poitou-Charentes 183 sièges du conseil régional 6 et 13 décembre 2015 Type d’élection Élections régionales Corps électoral et résultats Population 5 808 594 Inscrits au 1er tour 4 268 933 Votants au 1er tour 2 175 858 50,97 % Votes exprimés au 1er tour 2 068 761 Votes blancs au 1er...

Italian fencer (1926–2024) Irene CamberCamber in 1960Personal informationNationalityItalianBorn(1926-02-12)12 February 1926Trieste, ItalyDied23 February 2024(2024-02-23) (aged 98)Lissone, ItalyHeight169 cm (5 ft 7 in)Weight63 kg (139 lb)SportCountry ItalySportFencingEventFoilClubSS Cassa di Risparmio, Milan Medal record Olympic Games 1952 Helsinki Foil Individual 1960 Rome Foil Team World Championships 1953 Brussels Foil Individual 1957 Paris Foil Team 195...

