![]() マグヌス効果を表したGIFアニメーション。右から左への流れに対し、中心のローターを右回転させ始めると、ローター後方の流れが左上方へ変化し(青矢印)、下向きの力(赤矢印)が発生する。
マグヌス効果を表したGIFアニメーション。右から左への流れに対し、中心のローターを右回転させ始めると、ローター後方の流れが左上方へ変化し(青矢印)、下向きの力(赤矢印)が発生する。
マグヌス効果(マグヌスこうか、英: Magnus effect)とは、回転しながら進む物体にその進行方向に対して垂直の力(揚力)が働く現象を言う。マグナス効果とも呼ばれる。
ベンジャミン・ロビンス(Benjamin Robins)によって観察[1]された小銃から発射される球形の弾丸が曲がることを説明するにあたって、1852年にドイツの科学者ハインリヒ・グスタフ・マグヌスによってはじめて認識された。
原理
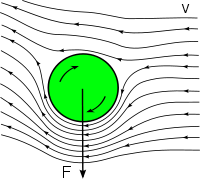
円柱または球の回転体が、粘性を有する流体中を一定速度で移動している、または一様流中に置かれた場合、円柱または球が回転している状態において、回転体の回転軸ベクトルと流体との相対速度ベクトルに垂直の方向に力が発生する。その大きさは、流体の密度、回転体と流体との相対速度、および回転体の回転速度に比例する。
定性的な説明:
例えば球をバックスピンで投げた場合、球を迂回する流体には、流速と流体の曲率半径による遠心力が働く。回転体の前面、風上側は流速が減少する代わりに圧力が増し、大気圧よりも増すので抗力となる。しかし、回転体近くの上下は共に、遠心力による圧力勾配が生じ、表面の気圧が大気圧よりも負となっている。さらに、球が回転しているとき、流体のせん断応力が関与する表面の境界層の流れと、回転体を迂回する主流には、回転体の座標から見て、コリオリの力が作用している。球の前面で流体の運動量がゼロ位置である淀み点から境界層の流れが上下に分かれ、その淀み点を境にしてコリオリ力は、上側では負となって遠心力に追加され、下側では正の圧力として遠心力から引かされる。その結果、負圧の絶対値が、上側>下側となり、その差が上向の揚力として顕在化することになる。
循環による説明:
今、2次元速度ポテンシャルを考えると、一定速度または一様流速度をU 、流体の密度をρとすれば、発生する力L は次式で得られる[2]。

上式は2次元ポテンシャルにおいて、循環を有する翼に生ずる揚力の式と一致する。この式はクッタ・ジュコーフスキーの定理と呼ばれる。
無次元式
より一般的に、粘性の効果も含めて次元解析により揚力L を求めると次式のようになる[3]。

ここで、
 :揚力係数
:揚力係数
 :回転速度比
:回転速度比
 :レイノルズ数
:レイノルズ数
ディンプルの効果
 ゴルフボールに刻まれたディンプル
ゴルフボールに刻まれたディンプル
ディンプル(表面のくぼみ)は、物体の臨界レイノルズ数を下げる。つまり、より低い速度で乱流が発生する。乱流は気流の物体表面からの剥離を防ぎ、マグヌス効果を維持する。
そのため、ディンプルはある範囲の速度で(ディンプル球の乱流発生速度から滑球の乱流発生速度まで)、マグヌス効果を増幅させる(マグヌス効果とは関係ないが、同時に、抗力を抑える効果もある)。
応用
 アントン・フレットナーのローター飛行機
アントン・フレットナーのローター飛行機
- ドイツの科学者アントン・フレットナーは、船に帆の代替として回転可能な円柱を取付けた船(ローター船)を設計・製造し、1926年5月9日に無事ニューヨークに到着し、大西洋横断の航海に成功した[3]。
- フレットナーによってローター飛行機が製造されたが飛行の記録は無い。
- 球技では、ボールがこの効果により落下が遅くなったり、はなはだしく浮き上がったりする。特に野球ボールでは回転の方向を通常(後ろ向き)から変えれば変化球となり、左右に曲がったり、重力の影響以上に落ちるなど、作用効果が著しい。
- 球体を投射する際にバックスピンをかけると、重力に逆らう揚力が生まれる。これを利用したものに、野球等における直球や、多くのBB弾を使用したエアソフトガンに搭載されている「ホップアップシステム」がある。
- この効果を応用した風車がロシアで開発され、風力発電に応用したスパイラルマグナス風車による発電方式が2007年に開発された[3]。
脚注
- ^ ジョン・D・アンダーソンJr. 著、織田剛 訳『空気力学の歴史』京都大学学術出版会、2009年、73頁。ISBN 978-4-87698-921-8。
- ^ 今井功『流体力学(前編)』(24版)裳華房、1997年、124頁。ISBN 4-7853-2314-0。
- ^ a b c 五十嵐保; 杉山均『流体工学と伝熱工学のための次元解析活用法』共立出版、2013年、65-68頁。ISBN 978-4-320-07189-6。
参考文献
- 谷 一郎『流れ学』(第三版)岩波全書、1967年。
- 清水 正之, 前田 昌信 著、笠原 英司(監修) 編『図解 流体力学の学び方』オーム社。
関連項目
外部リンク
- マグヌス効果の実験動画「Backspin Basketball Flies Off Dam」Veritasium