ポアソン核
|
Read other articles:

Institut Teknologi Keling KumangNama lainITKKJenisSwastaDidirikan2020 (2020)AfiliasiYayasan Pendidikan Keling KumangLokasiSekadau, Kalimantan Barat, IndonesiaKampusUrbanSitus webwww.itkk.ac.id Institut Teknologi Keling Kumang adalah sebuah perguruan tinggi swasta di Kabupaten Sekadau, Provinsi Kalimantan Barat, Indonesia. ITKK diresmikan oleh Bupati Sekadau, Rupinus dengan melakukan penandatanganan prasasti pada 9 Januari 2021.[1] Institut Teknologi Keling Kumang memiliki 3 progr...

Ettore Balestrero pada 2008 mengenakan jubah Ettore Balestrero (lahir 21 Desember 1966) adalah seorang prelatus Gereja Katolik Italia yang menjabat sebagai Nunsius Apostolik untuk Republik Demokratik Kongo. Ia sebelumnya menjabat sebagai Nunsius untuk Kolombia.[1] Referensi ^ Rinunce e Nomine, 10.08.2009 (Siaran pers) (dalam bahasa Italia). Holy See Press Office. 17 August 2009. Diakses tanggal 27 April 2019. Pengawasan otoritas Umum ISNI 1 VIAF 1 WorldCat Perpustakaan nasional ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. HelloPrint adalah pasar internasional terbesar untuk produk cetak.[1][2][3] Sejarah Helloprint didirikan pada tahun 2013 oleh Hans Scheffer, Michael Heerkens, Erwin Paaij dan Nick Goudriaan. Perusahaan ini didirikan sebagai Prin...

Mutsuki-class destroyer of the Imperial Japanese Navy sunk at Truk For other ships with the same name, see Japanese destroyer Fumizuki. Fumizuki in July 1926 History Empire of Japan NameFumizuki NamesakeJuly BuilderFujinagata Shipyards, Osaka Laid down20 October 1924 as Destroyer No. 29 Launched16 February 1926 Completed3 July 1926 RenamedAs Fumizuki, 1 August 1928 Stricken31 March 1944 FateSunk by American aircraft, 18 February 1944 General characteristics Class and typeMutsuki-class destro...

Tanaman pada fase pertumbuhan vegetatif Definisi Pertumbuhan Tanaman Secara umum, pertumbuhan didefinisikan sebagai proses pembelahan dan pemanjangan sel.[1] Pertumbuhan tanaman dalam arti terbatas menunjuk pada pertambahan ukuran yang tidak dapat balik, mencerminkan pertambahan protoplasma dan bobot kering pada tanaman.[1][2] Pertambahan bobot kering umumnya digunakan sebagai penunjuk ciri pertumbuhan karena pada umumnya hal tersebut mempunyai kepentingan ekonomi yang...

Norwegian footballer (born 1994) Jonas Grønner Personal informationDate of birth (1994-04-11) 11 April 1994 (age 29)Place of birth Bergen, NorwayPosition(s) DefenderSenior career*Years Team Apps (Gls)2011–2018 Brann 77 (7)2013 → KR (loan) 9 (0)2018–2022 Aalesund 73 (0)International career2011 Norway U17 5 (0)2013 Norway U19 6 (0)2014–2016 Norway U21 22 (1) *Club domestic league appearances and goals, correct as of 11:56, 27 August 2023 (UTC) Jonas Grønner (born 11 April 1994) i...

American comedy television series Tosh.0GenreComedyCreated by Daniel Tosh Mike Gibbons Directed byScott ZabielskiPresented byDaniel ToshCountry of originUnited StatesOriginal languageEnglishNo. of seasons12No. of episodes301 (list of episodes)ProductionExecutive producers Daniel Tosh George Lopez Charlie Siskel Christie Smith Running time21 minutesProduction companiesBlack Heart ProductionsComedy PartnersOriginal releaseNetworkComedy CentralReleaseJune 4, 2009 (2009-06-04) –Novemb...

NarjisMeninggalSamarraMakamSāmarrā, IraqSuami/istriAbu MuhammadAnakMuhammad al-Mahdi Bagian dari seri artikel mengenaiSyiah Peribadatan Penerus Nabi Muhammad Imamah Duka Muharram Tawassul Paham Kebohongan Ayatullah Arbain Hari perayaan Syiah Asyura Tabuik Arbain Maulud Idulfitri Iduladha Idulghadir Sejarah Ayat pemurnian Hadits dua hal berat Mubāhalah Khumm Rumah Fatimah Fitnah Pertama Fitnah Kedua Pembunuhan Ali Pertempuran Karbala Cabang-cabang Syiah Zaidiyah Syiah Dua Belas Imam Ja'far...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Communal constituencies – news · newspapers · books · scholar · JSTOR (March 2009) (Learn how and when to remove this message) Politics of Fiji Constitution History Executive President (list) Wiliame Katonivere Prime Minister Sitiveni Rabuka Cabinet Attorney-General Siromi Tura...
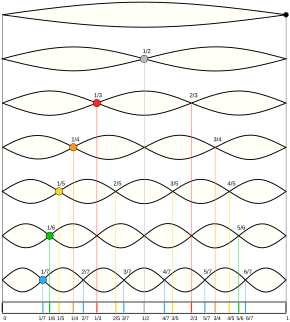
Application of acoustics to music Musical acoustics or music acoustics is a multidisciplinary field that combines knowledge from physics,[1][2][3] psychophysics,[4] organology[5] (classification of the instruments), physiology,[6] music theory,[7] ethnomusicology,[8] signal processing and instrument building,[9] among other disciplines. As a branch of acoustics, it is concerned with researching and describing the physics ...

Trap for catching humans Two mantraps (one a humane type) and a spring gun A mantrap is a mechanical physical security device for catching poachers and other trespassers.[1][unreliable source?] They have taken many forms, the most usual being similar to a large foothold trap, the steel springs being armed with teeth which meet in the victim's leg. In 1827, they were made illegal in England, except in houses between sunset and sunrise as a defence against burglars.[2]&#...

Questa voce sull'argomento cestisti tunisini è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Maherzia KsouriNazionalità Tunisia Altezza177 cm Pallacanestro RuoloAla Termine carriera2015 CarrieraSquadre di club 2007-2015CS Sfaxien Nazionale 2003 Tunisia U-212002-2009 Tunisia Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Maherzia Ksouri (Sfax, 21 febbraio 1982) è un'ex cestista tunisina. Carr...

British Liberal Democrat politician (1931–2022) The Right HonourableThe Lord FearnOBEFearn in 1987Member of the House of LordsLord TemporalIn office11 July 2001 – 11 July 2018 Life PeerageMember of Parliament for SouthportIn office1 May 1997 – 14 May 2001Preceded byMatthew BanksSucceeded byJohn PughIn office11 June 1987 – 16 March 1992Preceded byIan PercivalSucceeded byMatthew Banks Personal detailsBornRonald Cyril Fearn(1931-02-06)6 February 1931Southport, ...

Species of marsupial Small dorcopsis[1] Conservation status Near Threatened (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Infraclass: Marsupialia Order: Diprotodontia Family: Macropodidae Genus: Dorcopsulus Species: D. vanheurni Binomial name Dorcopsulus vanheurni(Thomas, 1922) Small dorcopsis range The small dorcopsis or lesser forest wallaby (Dorcopsulus vanheurni) is a species of marsupial in the fami...

Greece in the Roman era (Greek: Έλλάς, Latin: Graecia) describes the Roman conquest of ancient Greece (roughly, the territory of the modern nation-state of Greece) as well as that of the Greek people and the areas they inhabited and ruled historically.[1][2][3] It covers the periods when Greece was dominated first by the Roman Republic and then by the Roman Empire.[4] The provincial subdivision of Roman Greece In the history of Greece, the Roman era began...

Former municipality in Fribourg, SwitzerlandBarberêcheFormer municipalityBarberêche Castle Coat of armsLocation of Barberêche BarberêcheShow map of SwitzerlandBarberêcheShow map of Canton of FribourgCoordinates: 46°51′N 7°10′E / 46.850°N 7.167°E / 46.850; 7.167CountrySwitzerlandCantonFribourgDistrictSee/LacGovernment • ExecutiveConseil communal with 5 members • MayorSyndicArea[1] • Total9.13 km2 (3.53 s...

Prime Minister of the United Kingdom from 1905 to 1908 Campbell-Bannerman redirects here. For other people with this name, see Campbell-Bannerman (surname). The Right HonourableSir Henry Campbell-BannermanGCBPortrait by George Charles Beresford, 1902Prime Minister of the United KingdomIn office5 December 1905 – 3 April 1908MonarchEdward VIIPreceded byArthur BalfourSucceeded byH. H. AsquithLeader of the OppositionIn office6 February 1899 – 5 December 1905MonarchsVictoriaE...

Romanian soup This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ciorbă de perișoare – news · newspapers · books · scholar · JSTOR (March 2013) (Learn how and when to remove this message) Ciorbă de perișoareTypeSour soupPlace of originRomaniaMain ingredientsMeatballs (minced pork), rice, spices, ciorbă Cio...

Ponte alla CarraiaLocalizzazioneStato Italia AttraversaArno Coordinate43°46′12.87″N 11°14′50.09″E43°46′12.87″N, 11°14′50.09″E Dati tecniciTipoPonte ad arco Materialelegno e pietra Campate5 Lunghezza140 m Larghezza14 m RealizzazioneProgettistaEttore Fagiuoli Costruzione1218-1948 (ricostruzione) Inaugurazione1952 e 1948 CostruttoreEttore Fagiuoli Intitolato acarro Mappa di localizzazione Modifica dati su Wikidata · Manuale Il ponte alla Carraia, detto in passato a...

Highway in Manitoba Provincial Trunk Highway 31Route informationMaintained by Department of InfrastructureLength22 km (14 mi)Existed1959–presentMajor junctionsSouth end ND 1 (Maida–Windygates Border CrossingNorth end PTH 3 / PR 240 near Darlingford LocationCountryCanadaProvinceManitobaRural municipalitiesPembina Highway system Provincial highways in Manitoba Winnipeg City Routes ← PTH 30→ PTH 32 Provincial Trunk Highway 31 (PTH 31...


















=\int _{S}u(\zeta )P(x,\zeta )d\sigma (\zeta ).\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f033ebd415b71bb2dcff0067589db491795302c)



![{\displaystyle c_{n}={\frac {\Gamma [(n+1)/2]}{\pi ^{(n+1)/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ee22b30547375bb3247081cfc2717b90bc215c)


=[P(t,\cdot )*u](x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb627c3bda7bd1b596c31a2870c88e39d015cb71)