この項目では、形状モデリングのブーリアン演算について説明しています。ブール代数の演算については「ブール論理」をご覧ください。

ブーリアン演算（ブーリアンえんざん）または集合演算（しゅうごうえんざん）とは、3次元コンピュータグラフィックスやCAD等の形状モデリングにおいて、体積を持った形状（3次元の場合）を集合とみなし、複数の形状を和、差、積といった集合演算により組み合わせ、合成された形状を作る演算である。ソリッドモデリングの1手法であるCSG表現においては根幹的な技術となる。サーフェスモデラにおいても形状をソリッドモデルと仮定できる状況であれば使用できる場合がある。

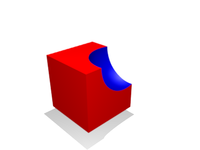
ブーリアン演算の例（青い球が右オペランドである）

和（${\displaystyle \cup }$）	差（${\displaystyle -\!}$）	積（${\displaystyle \cap }$）
他の形状と一体化するように働く。	他の形状を削るように働く。	他の形状と重なる部分を残すように働く。

2次元（平面）の多角形に対するブーリアン演算に関する話題。

• Vattiクリッピング法
• Sutherland–Hodgman法 (特殊ケースのアルゴリズム)
• Weiler–Athertonクリッピング法 (特殊ケースのアルゴリズム)

初期の多角形に対するブーリアン演算は頂点を使うのではなくビットマップをそのまま使用していた。多角形を扱うのにビットマップをそのまま使用するのは欠点がたくさんある。欠点の一つは、多角形を表現する際のピクセル数に比例して必要な計算量・メモリ量が増える。

近年の多角形に対するブーリアン演算は頂点を使った走査アルゴリズム^[1]を使用する。凸多角形に対するブーリアン演算は線形時間で計算可能^[2]である。

• Constructive Solid Geometry
• 論理演算
• ベン図

この項目は、コンピュータに関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（PJ:コンピュータ/P:コンピュータ）。

• 表示
• 編集