バーンスタイン多項式
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Ekor kuda – berita · surat kabar · buku · cendekiawan · JSTOR Gaya rambut ekor kuda dari samping Untuk membuat gaya rambut ekor kuda, beberapa, sebagian besar atau seluruh rambut di kepala ditarik jauh dari w...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. GouéckéSub-prefektur dan kotaGouéckéLokasi di GuineaKoordinat: 8°1′N 8°43′W / 8.017°N 8.717°W / 8.017; -8.717Koordinat: 8°1′N 8°43′W / 8.017°N 8.717°W / 8.017; -8.717Negara Guinea...

Dua Belas Lagu Islami Terbaik Vol. 3Album studio karya berbagai artisDirilis25 September 2007GenreIslamiLabelSony BMG IndonesiaKronologi Dua Belas Lagu Islami Terbaik Dua Belas Lagu Islami Terbaik Vol. 2 (2005)Dua Belas Lagu Islami Terbaik Vol. 22005 Dua Belas Lagu Islami Terbaik Vol. 3 (2007) Dua Belas Lagu Islami Terbaik Vol. 4 (2008)Dua Belas Lagu Islami Terbaik Vol. 42008 Dua Belas Lagu Islami Terbaik Vol. 3 adalah album kompilasi rohani Islam ketiga dari seri Dua Belas Lagu Islami Te...

منتخب سويسرا لكرة الطائرة للرجال الكنية ' كونفدرالية الاتحاد الأوروبي لكرة الطائرة [الإنجليزية] مراتب تصنيف فيفب 54 (في أكتوبر 2018) بطولة أوروبا المشاركات 1 (أولها في سنة 1971) أفضل نتيجة المركز التاسع عشر 1989 الموقع الرسمي [www.volleyball.ch] تعديل مصدري - تعديل منتخب سويسرا الوطني ل�...
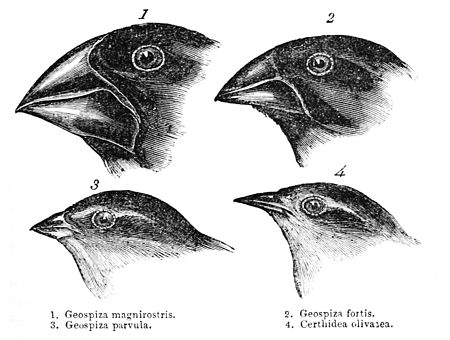
Параллельная эволюция или параллелизм (от греч. παράλληλος — параллельный; идущий рядом) — независимое развитие сходных признаков в эволюции близкородственных, но выделившихся групп организмов, протекающее в одном направлении. Предполагает наличие общего предка...

2012 single by Kylie MinogueFlowerSingle by Kylie Minoguefrom the album The Abbey Road Sessions Released25 September 2012RecordedAbbey Road Studios, London, EnglandGenreOrchestral pop[1]Length3:30LabelParlophoneSongwriter(s) Kylie Minogue Steve Anderson Producer(s) Steve Anderson Kylie Minogue singles chronology Timebomb (2012) Flower (2012) Limpido (2013) Music videoFlower on YouTube Flower is a song by Australian singer and songwriter Kylie Minogue. The song was originally written ...

Danish pop duo Ben and TanBen and Tan at the Dansk Melodi Grand Prix 2020Background informationOriginDenmarkGenresPopYears active2020 (2020)–presentMembers Benjamin Rosenbohm Tanne Balcells Ben and Tan are a Danish duo consisting of Benjamin Rosenbohm (born 3 June 2002) and Tanne Balcells (born 15 January 1998). They were due to represent Denmark in the Eurovision Song Contest 2020 in Rotterdam, with the song Yes, until it was cancelled due to the COVID-19 pandemic.[1][2 ...

Country within the United Kingdom This article is about the country. For other uses, see England (disambiguation). England FlagAnthem: VariousPredominantly God Save the King(National anthem of the United Kingdom)Location of England (dark green)– in Europe (green & dark grey)– in the United Kingdom (green)StatusCountryCapitaland largest cityLondon51°30′N 0°7′W / 51.500°N 0.117°W / 51.500; -0.117National languageEng...

Probability distribution Gamma Probability density function Cumulative distribution functionParameters k > 0 shape θ > 0 scale α > 0 shapeβ > 0 rateSupport x ∈ ( 0 , ∞ ) {\displaystyle x\in (0,\infty )} x ∈ ( 0 , ∞ ) {\displaystyle x\in (0,\infty )} PDF f ( x ) = 1 Γ ( k ) θ k x k − 1 e − x / θ {\displaystyle f(x)={\frac {1}{\Gamma (k)\theta ^{k}}}x^{k-1}e^{-x/\theta }} f ( x ) = β α Γ ( α...

У этого термина существуют и другие значения, см. Западный округ. Западный внутригородской округ город Краснодар Дата основания 1936 год Дата упразднения 1994 Прежние имена Кагановичский, Ленинский районы Микрорайоны Дубинка, Черёмушки, Покровка Площадь 22[1] км² Насе...

Anglican bishop For his son, the Anglican archdeacon, see Thomas Dealtry (son). 1922 published representation Christianity portalThe Rt Rev Thomas Dealtry (1795–1861) was an Anglican bishop in the 19th century.[1] Life He was born into a poor family in Knottingley in Yorkshire in 1796.[2] Mainly self-taught, Dealtry worked as an usher in a Doncaster school and then as tutor to a private family, where he eloped with the sister of his pupil in 1819. After she died, he married ...

نادي رأس تنورة السعودي شعار النادي الألوان الأزرق والأحمر تأسس عام 1396 هـ الملعب رأس تنورة السعودية البلد السعودية الدوري دوري الدرجة الثالثة السعودي 2015-2016 2015-2016 الإدارة المالك الهيئة العامة للرياضة رئيس النادي علي حمد بالحارث الامين العام حسن مسفر الخبيزي المدرب ط...

Human settlement in Yukon, Canada Gas station in Swift River Swift River is a settlement in the Canadian territory of Yukon, primarily a service stop on the Alaska Highway at historical mile 733. The radius of the area is estimated to be about 22.71 square kilometres (8.77 square miles)). The only permanent population owns and operates, or is employed at, the area's commercial highway establishment. Other residents are transient, working at the Yukon government's highway maintenance camp. Dem...

Open cluster in the constellation Tucana NGC 346James Webb Space Telescope image of NGC 346Observation data (J2000 epoch)Right ascension00h 59m 05.090s[1]Declination−72° 10′ 33.24″[1]Distance210,000 light-yearsPhysical characteristicsH II regionOther designationsESO 51-10,[2] N66AssociationsConstellationTucana[3]See also: Open cluster, List of open clusters NGC 346 is a young[4] open cluster of stars with associated neb...

State park in Oregon, United States South Beach State ParkPond in the parkTypePublic, stateLocationLincoln County, OregonNearest cityNewportCoordinates44°36′14″N 124°03′49″W / 44.6040063°N 124.0637291°W / 44.6040063; -124.0637291[1]Operated byOregon Parks and Recreation Department South Beach State Park is a state park in the U.S. state of Oregon, administered by the Oregon Parks and Recreation Department. It is near the unincorporated com...

Questa voce sull'argomento siti web è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Tom's Hardwaresito webURLwww.tomshardware.com/ Tipo di sitoBlog LinguaMultilingue Registrazionefacoltativa ProprietarioTechMediaNetwork, Inc. Lancio1996 Stato attualeattivo SloganThe authority on tech Modifica dati su Wikidata · Manuale Tom's Hardware è una testata giornalistica on-line di argomento tecnologico fondata nel 1996 dal dottor Thomas Pabst. Tom's Har...

Basilica prepositurale di Santa Maria presso San SatiroVeduta da via Torino.Stato Italia RegioneLombardia LocalitàMilano IndirizzoVia Torino Coordinate45°27′45.84″N 9°11′15.9″E45°27′45.84″N, 9°11′15.9″E Religionecattolica di rito ambrosiano Arcidiocesi Milano ArchitettoDonato Bramante, Giovanni Antonio Amadeo Stile architettonicorinascimentaleneorinascimentale (facciata)romanico (campanile) Inizio costruzione1478IX secolo (sacello di San Satiro) Completamento1483 (st...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Crossed Over – news · newspapers · books · scholar · JSTOR (June 2020) Canadian TV series or program Crossed OverFilm posterBased onCrossed Over: A Murder, A Memoirby Beverly LowryScreenplay byJohn WierickDirected byBobby RothStarringDiane KeatonJenni...

ICQTipePengirim pesan instan, layanan jejaring sosial, aplikasi seluler dan komunitas daring Versi pertama15 November 1996 Versi stabil 10.0.16100 (21 Februari 2022) GenreKlien Pengirim pesan instanLisensiAdwareBahasabanyak bahasa Karakteristik teknisSistem operasiMicrosoft Windows, macOS, Linux, iOS, Android, Windows Phone dan Symbian OS Formatunduhan digital Bahasa pemrogramanC++ Informasi pengembangPengembangMirabilis, AOLPenerbitGoogle Play dan App Store Sumber kode Kode sumberPranala Sna...

Questa voce o sezione sull'argomento Competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Si invita a seguire il modello di voce Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. SuperLiga 2013-2014Jelen SuperLiga 2013-2014 Competizione SuperLiga Sport Calcio Edizione 8ª Organizzatore FSS Date dal 10 agosto 2013al 28 maggio 2014 Luogo Serbia Partecipanti 16 Risultati Vincitore Ste...














![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)



![{\displaystyle b_{\nu ,n}(x)\geq 0\ for\ x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28972ddedc2afeab915f1fa3503ef81dd65360)
![{\displaystyle 0\leq x,\ 0\leq (1-x)\ for\ x\in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a9113cbb26a2b3b4e06a09bad9fd0849219cd6f)


















