スペクトル法
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Olah Raga Gulat dalam Upacara Kayo sebagai bentuk keperkasaan seorang laki-laki di Suku Dayak Bahau. Kayo adalah upacara adat Suku Dayak Bahau yang bermukim di Kabupaten Kutai Barat, Kalimantan Timur.[1] Upacara adat Kayo yang dilakukan sebagai...

Kapal jung Cina di Jepang, pada masa awal periode Sakoku (1644-1648, cetakan blok kayu Jepang). Sebuah hasil gravir Eropa abad ke-17 menggambarkan utusan pembawa upeti Belanda menuju kediaman Tokugawa. Dengan perubahan ke arah isolasionisme, bakufu berusaha menciptakan sistem upeti dengan model Tiongkok. Sakoku (鎖国code: ja is deprecated , harfiah: negara terkunci / negara terrantai) adalah kebijakan luar negeri Jepang, yang mengatur bahwa orang asing yang tidak diizinkan memasuki Jepang m...

Artikel ini bukan mengenai Kasih dan Amara. Amara Sahabat LangitGenre Drama Roman Melodrama Fantasi PembuatMD EntertainmentPemeran Prilly Latuconsina Shawn Adrian Denira Wiraguna Cinta Brian Naomi Paulinda Nadya Fricella Amara Bryan Mckenzie Justin Adiwinata Baron Yusuf Siregar Kevin Royano Rina Hasyim Dewi Rezer Ivan Fadilla Negara asalIndonesiaBahasa asliIndonesiaJmlh. musim1Jmlh. episode21 (daftar episode)ProduksiProduserManoj PunjabiPengaturan kameraTurpin SihombingDurasi60—90 menitRuma...

Irish politician (1880–1922) Seán HalesTeachta DálaIn officeJune 1922 – 7 December 1922In officeMay 1921 – June 1922ConstituencyCork Mid, North, South, South East and West Personal detailsBornJohn Hales(1880-03-30)30 March 1880Ballinadee, County Cork, IrelandDied7 December 1922(1922-12-07) (aged 42)Ormonde Quay, Dublin, IrelandRelativesTom Hales (brother)Military serviceBranch/serviceIrish Republican ArmyNational ArmyRankBrigadier generalBattles/warsIrish War of...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Australian electorate WakehurstNew South Wales—Legislative AssemblyInteractive map of district boundaries from the 2023 state electionStateNew South WalesCreated1962MPMichael ReganPartyIndependentNamesakeJohn Loder, 2nd Baron WakehurstElectors55,814 (2019)DemographicUrban Electorates around Wakehurst: Pittwater Pittwater Pacific Ocean Davidson Wakehurst Pacific Ocean Willoughby Manly Manly The Electoral district of Wakehurst is an electoral district of the Legislative Assembly in the ...

American boxer (1858–1918) Not to be confused with John L. O'Sullivan. For other uses, see John Sullivan. John L. SullivanSullivan in 1882BornJohn Lawrence Sullivan(1858-10-15)October 15, 1858Boston, Massachusetts, U.S.DiedFebruary 2, 1918(1918-02-02) (aged 59)Abington, Massachusetts, U.S.Other names Boston Strong Boy His Fistic Holiness StatisticsWeight(s) Heavyweight Height5 ft 10+1⁄2 in (179 cm)[1]Reach74 in (188 cm)StanceOrthodox Boxing r...
Governing body for the sport of cricket in Zimbabwe Zimbabwe CricketSportCricketJurisdictionNationalAbbreviationZCFounded1992; 32 years ago (1992)AffiliationInternational Cricket CouncilAffiliation date6 July 1992; 31 years ago (1992-07-06)Regional affiliationAfrica Cricket AssociationAffiliation date1997; 27 years ago (1997)HeadquartersHarare Sports Club, HarareLocationHarare, ZimbabweChairmanTavengwa Mukuhlani[1]CEOWilfred Mukond...

Chinese three-stringed lute This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sanxian – news · newspapers · books · scholar · JSTOR (November 2013) (Learn how and when to remove this message) SanxianThe Chinese sanxianTraditional Chinese三弦Simplified Chinese三弦TranscriptionsStandard MandarinHan...

1879 Portuguese legislative election ← 1878 19 October 1879 1881 → 137 seats to the Chamber of Deputies69 seats needed for a majority First party Second party Leader Anselmo José Braamcamp Fontes Pereira de Melo Party Progressive Regenerator Leader since 1876 1856 Last election 22 seats 97 seats Seats won 106 21 Seats after 84 76 Third party Fourth party PRP Leader José Dias Ferreira Political Directory Party Constituent ...

Cet article est une ébauche concernant une compagnie aérienne et Chypre. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Les entreprises étant sujet à controverse, n’oubliez pas d’indiquer dans l’article les critères qui le rendent admissible. Boeing 737 d'Eurocypria Airlines EuroCypria Airlines est une compagnie aérienne chypriote. Destinations EuroCypria Airlines dessert principalement l'Allemagne au départ de Paphos et de Larnaca. La flotte de la c...

У Вікіпедії є статті про інших людей із прізвищем Франк (прізвище). Сезар Франкфр. César FranckОсновна інформаціяПовне ім'яфр. César Auguste Jean Guillaume Hubert Franck[1]Дата народження10 грудня 1822(1822-12-10)[2][3][…]Місце народженняЛьєж, Об'єднане королівство Нідерландів[2][4][1&#...

Austríacos Bandeira da Áustria Mapa da diáspora austríaca ao redor do mundo. População total ca. 8–8,5 milhões Regiões com população significativa Áustria 6,75 milhões (2011)[a] Estados Unidos 684 184[1] Alemanha 345 620[2] Canadá 197 990[3] Austrália 45 530[4] Suíça 40 300–65 090[5][6][7] Reino Unido 21 600–25 000[6][7] França 20 000 [8][7] Itália 16 331 [7] Países Baixo...

Los libros de Oz forman una colección que comienza con El Maravilloso Mago de Oz, que relata la historia de la Tierra de Oz. Oz fue creada originalmente por el autor L. Frank Baum, quien escribió 14 libros sobre este mundo. La mayoría de los libros son sobre las aventuras de Dorothy y Baum -al igual que muchos autores posteriores- se llaman a sí mismos Historiadores reales de Oz, enfatizando el hecho de que Oz es un lugar genuino. Después de la muerte de Baum, más autores escribieron ot...

金沢市の行政機関金沢市教育委員会役職教育長 野口弘組織概要所在地 石川県金沢市柿木畠1番1号ウェブサイト 金沢市教育委員会ホームページテンプレートを表示 金沢市教育委員会(かなざわしきょういくいいんかい)は、石川県金沢市の教育委員会。金沢市内の教育に関連した調査などを行う行政委員会である。 概要 組織は教育総務課・学校職員課・学校指導課・�...
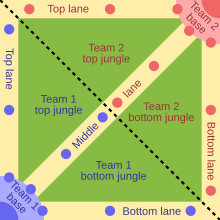
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: マルチプレイヤーオンラインバトルアリーナ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2015年5月) バッドアート�...

ييلابوغا شعار الاسم الرسمي (بالتتارية: Алабуга) الإحداثيات 55°46′00″N 52°02′00″E / 55.766666666667°N 52.033333333333°E / 55.766666666667; 52.033333333333 تاريخ التأسيس 1007 تقسيم إداري البلد روسيا[1][2] خصائص جغرافية المساحة 41 كيلومتر مربع ارتفاع 70 متر عد...

Deep and emotional extreme dislike For other uses, see Hatred (disambiguation). Hate redirects here. For other uses, see Hate (disambiguation). Hazel Massery yelling at Elizabeth Eckford in a display of racial hatred in 1957. Part of a series onEmotions Affect Classification In animals Emotional intelligence Mood Self-regulation Interpersonal Dysregulation Valence Emotions Acceptance Admiration Affection Amusement Anger Angst Anguish Annoyance Anticipation Anxiety Apathy Arousal Awe Belonging...

Українська Гельсінська спілка з прав людини(УГСПЛ)Дата заснування2004Типасоціація громадських правозахисних організаційАдреса04071, м. Київ, вул. Фролівська, 3/34, (3-й поверх)[1]Офіційний сайтhelsinki.org.ua Див. також: Українська Гельсінська Спілка та Українська Гельсінська �...

Desert basin west of the Nile south of Cairo, Egypt Site of Faiyum Oasis (directly southwest of Cairo, listed as Al-Fayyum) on a map of Egypt Map showing Faiyum Oasis The Faiyum Oasis (Arabic: واحة الفيوم Waḥet El Fayyum) is a depression or basin in the desert immediately west of the Nile river, 62 miles south of Cairo, Egypt. The extent of the basin area is estimated at between 1,270 km2 (490 mi2) and 1,700 km2 (656 mi2). The basin floor comprises fields water...



































