Unità immaginaria
|
Read other articles:

United States Navy facility in Iceland. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Naval Radio Transmitter Facility Grindavik – news · newspapers · books · scholar · JSTOR (September 2023) (Learn how and when to remove this template message) Aerial view of NRTF Grindavik Naval Radio Transmitter Facility...

Berkik rawa Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Charadriiformes Famili: Scolopacidae Genus: Gallinago Spesies: G. megala Nama binomial Gallinago megala(Swinhoe, 1861) Berkik rawa[2][3][4] (Gallinago megala) adalah sejenis burung perandai bermigrasi berukuran sedang yang memiliki paruh yang panjang. Burung ini memiliki bulu berwarna coklat kekuning-kuningan, hitam, dan p...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Wrackspurt adalah salah satu hewan gaib di serial Harry Potter karya J.K. Rowling. Wrackspurt tidak dapat dilihat telanjang mata. Mereka dapat melayang dalam telinga manusia dan membuat otak manusia tidak fokus. Manusia yang terserag infeksi akibat wr...

NgemplakKapanewonNegara IndonesiaProvinsiDaerah Istimewa YogyakartaKabupatenSlemanPemerintahan • PanewuSumariyah, S.Sos, M.SiKode Kemendagri34.04.11 Kode BPS3404110 Luas85 km km² Ngemplak (Jawa: ꦔꦼꦩ꧀ꦥ꧀ꦭꦏ꧀, translit. Ngemplak) adalah sebuah kapanewon di Kabupaten Sleman, Daerah Istimewa Yogyakarta, Indonesia. Daftar Panèwu (Camat) No. Nama Mulai menjabat Selesai menjabat 1 Prodjotanojo 1951 2 Drs. M. Mahmudi 3 Sudiro, BA 4 Drs. Wachdi Asrarudin 5 D...

Terminal BenowoTerminal Penumpang Tipe CPapan Nama Terminal BenowoLokasiJalan Raya Benowo, Kelurahan Benowo, Kecamatan Pakal, Kota Surabaya, Provinsi Jawa Timur, Kodepos 60195Kawasan Barat Surabaya IndonesiaKoordinat7°14′08″S 112°36′29″E / 7.235558°S 112.607978°E / -7.235558; 112.607978Koordinat: 7°14′08″S 112°36′29″E / 7.235558°S 112.607978°E / -7.235558; 112.607978Pemilik Pemerintah Kota SurabayaOperator Dinas Perh...
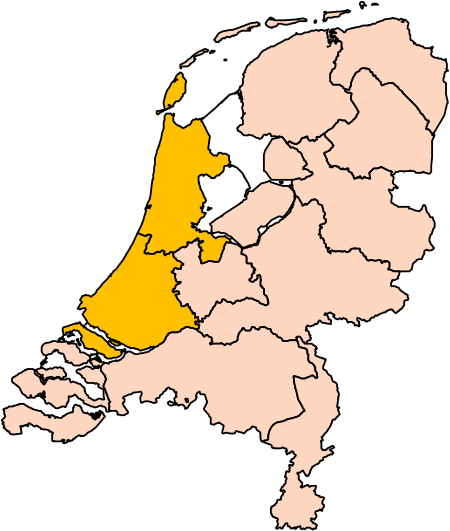
Pour les articles homonymes, voir Hollande (homonymie). Pour l’article ayant un titre homophone, voir Holland. Ne doit pas être confondu avec les Pays-Bas. Hollande-Septentrionale et Hollande-Méridionale (en jaune) dans les Pays-Bas européens actuels. La Hollande est une ancienne province des Pays-Bas divisée en 1840 en deux provinces distinctes : la Hollande-Septentrionale et la Hollande-Méridionale. Le nom de cette région historique provient du moyen néerlandais Holtland dés...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (juin 2012). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Pour les articles homonymes, voir Raimbourg. Dominiqu...

Former state electoral district of New South Wales, Australia Newcastle West was an electoral district of the Legislative Assembly in the Australian state of New South Wales. It was originally created in 1894, when multi-member districts were abolished,[1] and the three member district of Newcastle was divided between Newcastle West, Newcastle East, Kahibah, Waratah and Wickham.[2][3] It was abolished in 1904 as a result of the 1903 New South Wales referendum, which re...

Austrian zoologist (1903–1989) Konrad LorenzForMemRSLorenz in 1978BornKonrad Zacharias Lorenz(1903-11-07)7 November 1903Vienna, Austria-HungaryDied27 February 1989(1989-02-27) (aged 85)Vienna, AustriaNationalityAustrianAlma materColumbia UniversityUniversity of Vienna (MD, PhD)Awards ForMemRS (1964)[1] Kalinga Prize (1969) Nobel Prize in Physiology or Medicine (1973) Scientific careerFieldsEthology Konrad Zacharias Lorenz (German pronunciation: [ˈkɔnʁaːt tsaxaˈʁi...

Cheppes-la-PrairiecomuneCheppes-la-Prairie – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementChâlons-en-Champagne CantoneChâlons-en-Champagne-3 TerritorioCoordinate48°50′N 4°28′E / 48.833333°N 4.466667°E48.833333; 4.466667 (Cheppes-la-Prairie)Coordinate: 48°50′N 4°28′E / 48.833333°N 4.466667°E48.833333; 4.466667 (Cheppes-la-Prairie) Superficie19,6 km² Abitanti184[1] (2009) Dens...

متحف السرايا الحمراء إحداثيات 32°53′45″N 13°10′49″E / 32.89583333°N 13.18027778°E / 32.89583333; 13.18027778 معلومات عامة الموقع طرابلس الدولة ليبيا[1] سنة التأسيس 1919 تاريخ الافتتاح الرسمي 1919 معلومات أخرى تعديل مصدري - تعديل 32°53′45″N 13°10′49″E / 32.89583°N 1...

Divine belief in one's responsibility for the world This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Stewardship theology – news · newspapers · books · schol...

Mansion in Medina, Washington Bill Gates' houseGeneral informationArchitectural stylePacific lodgeLocationMedina, Washington, United StatesCoordinates47°37′40″N 122°14′31″W / 47.62774°N 122.24194°W / 47.62774; -122.24194Technical detailsStructural systemEarth-sheltered home Bill Gates designed and owns a mansion that overlooks Lake Washington in Medina, Washington. The 66,000-square-foot (6,100 m2) mansion[1] incorporates technology in its desi...

AramengoKomuneComune di AramengoNegaraItaliaWilayah PiedmontProvinsiProvinsi Asti (AT)Luas • Total11,4 km2 (44 sq mi)Ketinggian369 m (1,211 ft)Populasi (Desember 2004) • Total639 • Kepadatan5,6/km2 (15/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos14020Kode area telepon0141 Aramengo adalah komune yang terletak di distrik Provinsi Asti, Italia. Kota Aramengo memiliki luas sebesar 11,4&#...

Bärandeordningen för svenska ordnar och medaljer är ordnad i tolv grupper från A till L. Inom varje grupp guld före silver, silver före brons. I vissa fall är järn den högsta valören.[1][2] Bärandeordningen Officiella utmärkelser A. Kungliga Serafimerorden Huvudartikel: Serafimerorden B. Krigsdekorationer Huvudartikel: Svenska krigsdekorationer Riddare med stora korset av Svärdsorden Medaljen För tapperhet i fält Medaljen För tapperhet till sjöss Svärdsordens krigsko...

Buenos Aires Underground station RetiroGeneral informationLocationRamos Mejía and LibertadorCoordinates34°36′11″S 58°22′13″W / 34.6030°S 58.3702°W / -34.6030; -58.3702PlatformsSide platformsConnectionsMitre Line, Belgrano Norte Line and San Martín LineHistoryOpened3 June 2019Services Preceding station Buenos Aires Underground Following station Catalinastowards Plaza de los Virreyes Line ETransfer to: Retiro Terminus Retiro is the terminus station on Line ...

Yearbook published in 1822 Forget-Me-Not Covers of the first editionAuthorVariousOriginal titleForget-Me-Not: A Christmas and New Years Present for 1823LanguageEnglishGenreLiterary annualPublisherRudolf AckermannPublication dateNovember 1822Publication placeEnglandMedia typeDuodecimo (hardback)Pagesc. 390 Forget-Me-Not was an illustrated British annual published by Rudolph Ackermann. It was the first literary annual in English[1] and it was edited by Frederic Shoberl from it...

Leningrad Front“Para prajurit di Front Leningrad sebelum sebuah serangan” Para prajurit di parit-parit Front Leningrad sebelum sebuah serangan.Aktif1941–1945Negara Uni SovietCabang Tentara MerahTipe unitKomando Grup Angkatan DaratJumlah personelSeveral Angkatan DaratPertempuranPerang Dunia IIPengepungan LeningradSerangan BaltikPertempuran CourlandTokohTokoh berjasaGeorgy ZhukovLeonid Govorov Front Leningrad (bahasa Rusia: Ленинградский фронт) dibentuk pada 194...

Clemente VII Retrato por Sebastiano del Piombo(c. 1531, Museo J. Paul Getty de Los Ángeles) Papa de la Iglesia católica 19 de noviembre de 1523-25 de septiembre de 1534Predecesor Adriano VISucesor Paulo IIIInformación religiosaOrdenación sacerdotal 19 de diciembre de 1517Ordenación episcopal 21 de diciembre de 1517 por León XProclamación cardenalicia 23 de septiembre de 1513 por León XInformación personalNombre Julio de MédiciNacimiento 26 de mayo de 1478Florencia, República ...

Groupings of highly centralized criminal enterprises For other uses, see Organized crime (disambiguation). Crime Ring redirects here. For the 1938 American film, see Crime Ring (film). Criminology and penology Theory Anomie Biosocial criminology Broken windows Collective efficacy Crime analysis Criminalization Differential association Deviance Expressive function of law Labeling theory Psychopathy Rational choice Risk & actuarial criminology Social control Social learning Strain Subcultur...










![{\displaystyle \mathbb {R} [x]/(x^{2}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0ade67281f83ef6b6b7f43bf783c081adb1fc3)






![{\displaystyle \mathbb {C} =\mathbb {R} [x]/(x^{2}+1)=\mathbb {R} [i].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d48ae02374e17ce56ea934e997568eb634194bf9)

















































![{\displaystyle {\sqrt[{n}]{i}}=\cos {\left({\frac {\pi }{2n}}+{\frac {2\pi k}{n}}\right)}+i\sin {\left({\frac {\pi }{2n}}+{\frac {2\pi k}{n}}\right)}\qquad k=0,1,2,\dots ,n-1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372b6f79c8d52da558d7b527844ed616c5b472b5)












