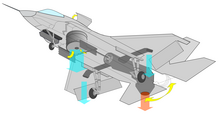
Ugello di scarico
|
Read other articles:

DarwiniusRentang fosil: Eocene, 47 jtyl PreЄ Є O S D C P T J K Pg N ↓ Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Primates Famili: Notharctidae Subfamili: Cercamoniinae Genus: Darwinius Spesies: D. masillae Nama binomial Darwinius masillaeFranzen et al., 2009 Darwinius adalah genus adalah primata yang hidup pada masa Eosen, sekitar 47 juta tahun yang lalu. Hanya terdapat satu spesies yang telah ditemukan, yaitu Darwinius masillae. Nama Darwin...

Hamantashprune hamantashen buatan rumahJenisKue atau pastriTempat asalKomunitas Yahudi Ashkenazi. Sekarang sebagian besar di Israel dan Amerika Serikat.VariasiIsian: biasanya biji poppySunting kotak info • L • BBantuan penggunaan templat ini Hamantash (bahasa Yiddi: המן טאש, juga disebut hamentasch, pl. hamantashen atau hamentaschen; (Ibrani) oznei Haman) adalah sebuah kue atau pastri isi yang dikenal karena bentuk segitiganya, biasanya dikaitkan dengan hari raya Yahud...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. August LandmesserLahirTanggal tidak terbaca. Angka tahun harus memiliki 4 digit (gunakan awalan nol untuk tahun < 1000).Moorrege, Schleswig-Holstein, Kekaisaran JermanMeninggalNot recognized as a date. Years must have 4 digits (use leading zeros fo...

Jamaah Ansharut TauhidLogo JATAmirUst. Sholeh IbrahimMarkasJl. Semenromo No.15.B RT.02/21, SukoharjoJumlah anggota300 (perkiraan)Dicap sebagai organisasi teror oleh Perserikatan Bangsa-Bangsa Amerika Serikat Bahrain Indonesia[1] Jepang Malaysia Selandia BaruSitus webSitus web resmi JAT Jamaah Ansharut Tauhid atau (JAT) adalah sebuah organisasi Islam di Indonesia. Organisasi ini merupakan pecahan dari Majelis Mujahidin Indonesia. Organisasi ini te...

State highway in western Missouri Route 152MO 152 highlighted in redRoute informationMaintained by MoDOTLength16.875 mi[1] (27.158 km)Major junctionsWest end I-435 / Route N in ParkvilleMajor intersections I-29 / US 71 in Kansas City US 169 in Kansas City Route 1 near Gladstone I-435 west of Liberty I-35 / US 69 / Route 110 (CKC) in Liberty East end Route 291 in Liberty LocationCountryUnited StatesStateMis...

Türkiye 1.Lig 1992-1993 Competizione Türkiye 1.Lig Sport Calcio Edizione 35ª Organizzatore TFF Luogo Turchia Partecipanti 16 Formula Girone unico Sito web tff.org Risultati Vincitore Galatasaray(9º titolo) Retrocessioni Bakırköyspor Aydınspor Konyaspor Statistiche Miglior marcatore Tanju Çolak (27) Incontri disputati 240 Gol segnati 716 (2,98 per incontro) Cronologia della competizione 1991-92 1993-94 Manuale L'edizione 1992-1993 della Türkiye 1...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Markus 1Permulaan Injil Markus pada Codex Boreelianus (abad ke-9/ke-10).KitabInjil MarkusKategoriInjilBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen2← Matius 28 pasal 2 → Markus 1 (disingkat Mrk 1 atau Mr 1) adalah pasal pertama dari Injil Markus dalam Perjanjian Baru di Alkitab Kristen, yang diyakini ditulis menurut catatan Markus berdasarkan kesaksian Simon Petrus, salah seorang dari Keduabelas Rasul Yesus Kristus.[1] Catatan Injil ini tidak dimulai denga...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2013) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding cita...

Pasukan Marinir 2Berkas:Logo Pasmar 2.pngLambang Pasukan Marinir 2Dibentuk22 Maret 2001NegaraIndonesiaCabangTNI Angkatan LautTipe unitSatuan Tempur MaritimPeranPasukan Senapan AmfibiBagian dariKorps MarinirMarkasSidoarjo, Jawa TimurJulukanPasmar 2MotoRaksa Nusantara CaktiBaretUnguMaskotBurung RajawaliUlang tahun22 MaretSitus webpasmar2.netTokohKomandan saat iniBrigadir Jenderal TNI (Mar) Muhammad Nadir, M.Tr.Opsla.Wakil komandanKolonel Mar Edi Prayitno Pasukan Marinir 2 atau (Pasmar 2) merupa...

Former hotel in Central, Hong Kong Hong Kong HiltonGeneral informationLocation2 Queen's Road, Central, Hong KongOpening1963ClosedMay 1,1995; 29 years ago (May 1,1995)OwnerHutchison WhampoaManagementHilton Hotel CorporationTechnical detailsFloor count26Design and constructionArchitecture firmPalmer and TurnerOther informationNumber of rooms750demolished to make way for Cheung Kong Centre Hong Kong Hilton was a hotel in Central, Hong Kong. Built in 1963, the 26-storey hotel was ini...

В Википедии есть статьи о других людях с именем Селевк. Селевк II Каллиникдр.-греч. Σέλευκος Β' Καλλίνικος Царь государства Селевкидов 246—225 год до н. э. Предшественник Антиох II Теос Преемник Селевк III Керавн Рождение 265 до н. э.(-265)неизвестно Смерть 225 до н. э.(-225)неизвестно Род...

Like & SharePoster resmiSutradaraGina S. NoerProduser Chand Parwez Servia Gina S. Noer Ditulis olehGina S. NoerPemeran Aurora Ribero Arawinda Kirana Aulia Sarah Jerome Kurnia Penata musikAria PrayogiSinematograferDeska BinarsoPenyuntingAline JusriaPerusahaanproduksi Starvision Plus Wahana Kreator Nusantara Tanggal rilis 8 Desember 2022 (2022-12-08) (Indonesia) 27 Januari 2023 (2023-01-27) (Festival Film Internasional Rotterdam) 23 April 2023 (2023-04-23) (...

Tsung-Dao Lee Tsung-Dao Lee (李政道 Pinyin: Lǐ Zhèngdào) (lahir 24 November 1926) ialah fisikawan Tiongkok–Amerika Serikat yang berkarya pada fisika partikel energi tinggi, asas simetri, dan mekanika statistik. Pada 1957, pada usia 31, Lee menerima Hadiah Nobel untuk karyanya pada pelanggaran hukum keseimbangan, dengan Chen Ning Yang, yang secara eksperimental dibuktikan oleh Chien-Shiung Wu. Lee dan Yang merupakan orang-orang Tionghoa pertama yang memenangkan Hadiah Nobel. Kota kedia...

This article may be unbalanced toward certain viewpoints. Please improve the article by adding information on neglected viewpoints, or discuss the issue on the talk page. (November 2017) Ethiofencarb Line structure of ethiofencarb Space-filling model of ethiofencarb Names Preferred IUPAC name 2-[(Ethylsulfanyl)methyl]phenyl methylcarbamate Other names Carbamic acid, methyl-, 2-(ethylthiomethyl)phenyl ester , Croneton , Ethiofencarb , Ethiofencarb , ethiophencarbe , Ethiophencarp , HOX 1901 , ...

لواء بلعما - لواء - تقسيم إداري البلد الأردن [1] المحافظة محافظة المفرق إحداثيات 32°12′43″N 36°06′53″E / 32.21192°N 36.11462°E / 32.21192; 36.11462 السكان التعداد السكاني 35599 نسمة (إحصاء 2015) • الذكور 18979 • الإناث 16620 • عدد الأسر 7123 الرمز الجغرافي 8623793&#...

Werner von HaeftenPengabdianJermanDinas/cabangWehrmachtLama dinas1939–1944PangkatOberleutnantPerang/pertempuranPerang Dunia Kedua Werner Karl von Haeften (9 Oktober 1908 – 21 Juli 1944) adalah seorang Oberleutnant di Wehrmacht. Ia mengambil bagian dalam konspirasi melawan Adolf Hitler yang dikenal sebagai Plot 20 Juli. Kehidupan Pribadi Haeften dan saudaranya, Hans lahir di Berlin dari Hans von Haeften, seorang perwira tentara dan Presiden Reichsarchiv. Ia belajar hukum...

Part of mathematics that addresses the stability of solutions For the branch of model theory, see stable theory. Stability diagram classifying Poincaré maps of linear autonomous system x ′ = A x , {\displaystyle x'=Ax,} as stable or unstable according to their features. Stability generally increases to the left of the diagram.[1] Some sink, source or node are equilibrium points. In mathematics, stability theory addresses the stability of solutions of differential equations and...

Mexican footballer (born 1998) For other people named Juan Sánchez, see Juan Sánchez (disambiguation). In this Spanish name, the first or paternal surname is Sánchez and the second or maternal family name is Purata. Juanjo Purata Sánchez in 2023Personal informationFull name Juan José Sánchez PurataDate of birth (1998-01-09) 9 January 1998 (age 26)Place of birth San Luis Potosí, MexicoHeight 1.81 m (5 ft 11 in)[1]Position(s) Centre-backTeam informatio...

Colonial Times in Spanish Empire La SerenaValparaísoRobinson Crusoe IslandPenco (Old Concepción)TalcahuanoCorral Bay (Valdivia)AncudTenquehuénclass=notpageimage| Map with places that were fortified at some point during colonial times. Blue dots mark locations first fortified in the 17th century or before. Green dots marks paces first fortified in the 18th century. In Colonial times the Spanish Empire diverted significant resources to fortify the Chilean coast as a consequence of Dutch and ...














![{\displaystyle \mathrm {Ma} _{g}={\sqrt {{\frac {1}{\delta }}\left[\left({\frac {p_{0}}{p_{g}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right]\,}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1b4714c781ae480e41fef21a312ffb3c39a1d2b)
![{\displaystyle {\dot {m}}={\frac {p_{g}\,A_{g}}{\sqrt {{\frac {RT_{g}}{\gamma }}\,}}}{\sqrt {{\frac {1}{\delta }}\left[\left({\frac {p_{0}}{p_{g}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right]\,}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07bd33777ec72b5da3ecf5f0221406ed8bc8d9ca)


![{\displaystyle {\frac {d}{d\left({\frac {p_{g}}{p_{0}}}\right)}}\left[\left({\frac {p_{g}}{p_{0}}}\right)^{\frac {2}{\gamma }}\left(1-\left({\frac {p_{g}}{p_{0}}}\right)^{\frac {\gamma -1}{\gamma }}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b5e8ca70ec551597f27a47d4ae6d890cc1ff1a5)








