Prominenza topografica
|
Read other articles:

Wright pada 2018 Jeremy Paul Wright MP QC (lahir 24 Oktober 1972) adalah seorang pengacara dan politikus asal Inggris yang menjabat sebagai Menteri Digital, Budaya, Media dan Olahraga dari 2018 sampai 2019. Sebagai anggota Partai Konservatif, ia menjadi anggota parlemen mewakili Kenilworth dan Southam sejak 2010, Referensi Pranala luar Wikimedia Commons memiliki media mengenai Jeremy Wright. www.jeremywright.org.uk Jeremy Wright's website Profile at the Conservative Party Profil di Parlem...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Gelora Group (A World Class Company) adalah sebuah perusahaan besar di Indonesia yang dipimpin oleh Direktur Utama Ibu Laniati Dewi. Grup ini memulai usaha pada bidang Migas, kemudian terus berkembang dan merambah ke berbagai bidang seperti perhotelan,...
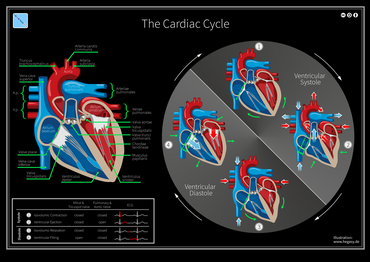
Performance of the human heart Cardiac cycleOrganismsAnimaliaBiological systemCirculatory systemHealthBeneficialActionInvoluntaryMethodBlood is allowed to enter relaxed ventricle chamber from vein through venous valve. Heart muscle contracts ventricle and blood is expelled through arterial valve to artery.OutcomeCirculation of blood per minute (Humans)Duration0.6–1 second (Humans)*Animalia with the exception of Porifera, Cnidaria, Ctenophora, Platyhelminthes, Bryozoan, Amphioxus. The cycle ...

Dejan Kulusevski Kulusevski pada tahun 2019Informasi pribadiNama lengkap Dejan KulusevskiTanggal lahir 25 April 2000 (umur 23)Tempat lahir Stockholm, SwediaTinggi 1,86 mPosisi bermain GelandangInformasi klubKlub saat ini Tottenham HotspurNomor 21Karier junior2006–2016 Brommapojkarna2016–2019 AtalantaKarier senior*Tahun Tim Tampil (Gol)2018–2020 Atalanta 3 (0)2019–2020 → Parma (pinjaman) 17 (4)2020 - 2022 Juventus 74 (9)2020 → Parma (pinjaman) 19 (6)2022–2023 → Totenham H...

German economist Uwe ReinhardtBornSeptember 24, 1937Osnabrück, GermanyDiedNovember 14, 2017(2017-11-14) (aged 80)Princeton, New Jersey, United StatesScientific careerDoctoral advisorRichard Ruggles[1] Uwe Ernst Reinhardt (September 24, 1937 – November 14, 2017) was a professor of political economy at Princeton University and held several positions in the healthcare industry.[2] [3] Reinhardt was a prominent scholar in health care economics and a frequent speake...

Compianto sul Cristo morto, pietra calcare, 1554-64, chiesa di Saint Etienne a Saint-Mihiel Ligier Richier (Saint-Mihiel, 15 settembre 1500 – Ginevra, 8 agosto 1567) è stato uno scultore francese che adottò, su un fondamento di cultura gotica, i modi stilistici del primo Rinascimento. Al servizio della corte del duca di Lorena, realizzò numerose ed importanti opere che oggi si conservano soprattutto nei dipartimenti della Mosa e della Meurthe e Mosella, nella regione della Lorena. Indic...

Radio or TV service, 100W or less Low-power radio redirects here. For other low-power radio-wave communications, see Near-field communication and Low-power wide-area network. An LPAM antenna in a beer tent Low-power broadcasting is broadcasting by a broadcast station at a low transmitter power output to a smaller service area than full power stations within the same region. It is often distinguished from micropower broadcasting (more commonly microbroadcasting) and broadcast translators. LPAM...

Bus station in Johor Bahru, Malaysia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Larkin Sentral – news · newspapers · books · scholar · JSTOR (May 2017) (Learn how and when to remove this message) 1°29′44.7″N 103°44′33.7″E / 1.495750°N 103.742694°E / 1.495750; 103.7426...

British politician The Right HonourableThe Lord BarnettPCBarnett's last appearance at House of Lords questions.Chair of the Public Accounts CommitteeIn officeJuly 1979 – 9 June 1983Preceded byEdward du CannSucceeded byRobert SheldonShadow Chief Secretary to the TreasuryIn office4 May 1979 – 14 July 1979LeaderJames CallaghanChief Secretary to the TreasuryIn office5 March 1974 – 4 May 1979Prime MinisterHarold WilsonJames CallaghanPreceded byTom BoardmanSucceeded...

Voce principale: Ravenna Football Club 1913. Unione Sportiva RavennaStagione 1987-1988Sport calcio Squadra Ravenna Allenatore Francesco Brignani dalla 15ª Gilberto Alvoni Presidente Giuseppe Cannillo Serie C211° Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Mirco Fantini (34) Miglior marcatoreCampionato: Mezzini (11) StadioStadio Bruno Benelli 1986-1987 1988-1989 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Unione Sportiva Ravenna...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Robin Gosens Gosens pada 2018Informasi pribadiNama lengkap Robin Everardus Gosens[1]Tanggal lahir 5 Juli 1994 (umur 29)Tempat lahir Emmerich am Rhein, JermanTinggi 1,83 m (6 ft 0 in)[2]Posisi bermain Gelandang kiri, Bek sayap kiri[3][4]Informasi klubKlub saat ini Union BerlinNomor 6Karier junior2000–2007 Fortuna Elten2007–2009 1. FC Bocholt2009–2012 VfL Rhede2012–2014 VitesseKarier senior*Tahun Tim Tampil (Gol)2014–2015 Vitesse 0 ...

Muslim JamaikaTotal populasi1.000[1]AgamaIslam Sunni, Islam Syiah dan AhmadiyahBahasaBahasa utama yang digunakan adalah Bahasa Inggris, Patwa Jamaika, Arab, UrduIslam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagask...

American baseball umpire (born 1981) Baseball player David RackleyRackley as a Minor League umpire, 2006Born: (1981-10-11) October 11, 1981 (age 42)Houston, Texas, U.S.MLB debutAugust 13, 2010 Crew InformationUmpiring crew3Crew members#27 Larry Vanover (crew chief)#87 Scott Barry#86 David Rackley#96 Chris Segal Career highlights and awardsSpecial assignments All-Star Games (2021) Wild Card Games/Series (2016, 2017, 2019, 2020) Division Series (2020, 2022, 2023) League Championship Series...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) الاتحاد التاهيتي لكرة القدم (بالفرنسية: Fédération tahitienne de football) الاسم المختصر TFA الرياضة كرة القدم أسس ع...

South African tennis player For other people with the same name, see Kevin Anderson. Kevin AndersonAnderson at the 2021 French OpenCountry (sports) South AfricaResidenceGulf Stream, Florida, U.S.Johannesburg, South AfricaBorn (1986-05-18) 18 May 1986 (age 38)Johannesburg, South AfricaHeight2.03 m (6 ft 8 in)Turned pro2007PlaysRight-handed (two-handed backhand)CollegeUniversity of IllinoisCoachDiego Moyano Jay BosworthPrize moneyUS$17,791,917[1] ...

This is a list of Hindu members of the United States Congress. As of 2023[update], three practicing Hindus have been elected to Congress, the first being Tulsi Gabbard in 2013. In total, eight members of Congress have been either practicing Hindus or born into Hindu families but adhering to other religions. Two practicing Hindus currently serve in the United States House of Representatives. Senate Further information: Religious affiliation in the United States Senate No Hindu has eve...

كأس الإمبراطور 2012 تفاصيل الموسم كأس الإمبراطور النسخة 92 البلد اليابان المنظم اتحاد اليابان لكرة القدم البطل كاشيوا ريسول مباريات ملعوبة 87 عدد المشاركين 88 كأس الإمبراطور 2011 كأس الإمبراطور 2013 تعديل مصدري - تعديل كأس الإمبراطور 2012 (بالي...

The City of Ember PengarangJeanne DuprauNegaraUnited StatesBahasaEnglishGenrePost-apocalyptic, science fiction, children's literatureTanggal terbitMay 2003Jenis mediaPrint (Hardcover and Paperback),digital (DVD)Halaman270ISBNISBN 0-375-82273-9OCLC50166630Desimal Dewey[Fic] 21LCCPZ7.D927 Ci 2003Diikuti olehThe People of Sparks The City of Ember adalah judul novel fiksi ilmiah karya Jeanne DuPrau yang dipublikasikan pada tahun 2003. Seperti karya Suzanne Martel berjudu...

Path for mostly non-motorized travel through a natural area This article is about paths, tracks or other routes used for recreational travel. For other uses, see Trail (disambiguation). Trails redirects here. For the video game series, see Trails (series). A country track, or fieldway, in Slovenia Mountain bike trail in the Forest of Dean, England Trail in the Kruununpuisto Nature Park in Imatra, Finland A trail, also known as a path or track, is an unpaved lane or a small paved road not inte...

