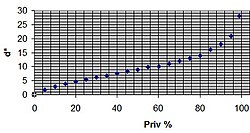
Probabilità di scoperta sonar e distanza dal bersaglio
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2024. Landasan Udara BatujajarIATA: noneICAO: WIPDInformasiJenisMiliterLokasiBatujajar, Jawa BaratZona waktuUTC+7Koordinat{{{coordinates}}} Landasan Udara Batujajar adalah bandar udara yang bernama Lapangan Udara Suparlan terletak di kecamatan Batujajar, Kabup...

MulutSkema melintang mulut, hidung, faring, dan laringPengidentifikasiMeSHD009055TA98A05.1.00.001TA2119, 2774FMA49184Daftar istilah anatomi[sunting di Wikidata] Mulut adalah suatu rongga terbuka tempat masuknya makanan dan air. Mulut biasanya terletak di kepala dan umumnya merupakan bagian awal dari sistem pencernaan lengkap yang berakhir di anus. Mulut terdiri dari gigi dan lidah. Bagian-bagian yang terdapat dalam mulut: Gigi (dens), Gigi fungsinya untuk menggigit, mengunyah, mencabik. G...

Patton OswaltOswalt di tahun 2017Lahir27 Januari 1969 (umur 55)Portsmouth, Virginia, A.S.AlmamaterCollege of William & Mary (BA)Pekerjaan Stand-up komedian aktor penulis Tahun aktif1988–sekarangSuami/istriMichelle McNamara (m. 2005; meninggal Kesalahan ekspresi: Operator < tak terduga) Meredith Salenger (m. 2017)Anak1Karier komediMediaStand-uptelevisionfilmGenreKomedi observasionalkomedi hit...

Australian politician The HonourableMatthew SwinbournMLCMatthew Swinbourn at Serpentine National ParkParliamentary Secretary to the Attorney-General; Minister for Electoral AffairsIncumbentAssumed office 19 March 2021MinisterJohn QuigleyMember of the Western Australian Legislative Council for East Metropolitan RegionIncumbentAssumed office 22 May 2017 Personal detailsBorn (1975-04-03) 3 April 1975 (age 49)Middle Swan, Western AustraliaPolitical partyLaborAlma materUniversity of W...

في الإسلام، يقدم الممرضون خدمات الرعاية الصحية للمرضى والأسر والمجتمعات كدليل على حب الله ومحمد. مهنة التمريض ليست جديدة على الإسلام. تشمل التقاليد الإسلامية التعاطف والمسؤولية تجاه المحتاجين.[1] ظهر هذا المنظور خلال تطور الإسلام كدين وثقافة وحضارة. أول ممرضة في الإسل...

Place in Boyacá Department, ColombiaVilla de LeyvaChurch of Nuestra Señora del Rosario FlagSealNickname(s): Villa de Nuestra Señora de Santa María de LeyvaLocation of the town of Villa de Leyva and the Leyva municipality in Boyacá DepartmentCoordinates: 5°38′N 73°32′W / 5.633°N 73.533°W / 5.633; -73.533Country ColombiaDepartmentBoyacá DepartmentProvinceRicaurte ProvinceFoundedJune 12, 1572Founded byAndré Diaz Venero de LeyvaGovernment •&...

Fyodor Adrianovich FuntikovFuntikov as photographed at the court, 1926.Chairman of the Trans-Caspian GovernmentIn office12 July 1918 – 15 January 1919Preceded byPosition established Succeeded byPosition abolished Personal detailsBorn1875Died5 May 1926Baku, Azerbaijan SSRPolitical partySocialist Revolutionary Party Fyodor Adrianovich Funtikov (Russian: Фёдор Адриа́нович Фу́нтиков; 1875/76 – 5 May 1926) was Chairman of Provisional Executive Committee of th...

Artikel ini tentang fisikawan Austria-Swiss Wolfgang Pauli. Untuk fisikawan Jerman, dan salah satu penemu penjebak ion, lihat Wolfgang Paul Wolfgang PauliLahirWolfgang Ernst Pauli(1900-04-25)25 April 1900Wina, Austria-HungariaMeninggal15 Desember 1958(1958-12-15) (umur 58)Zürich, SwissKebangsaanAustriaWarga negaraSwissAlmamaterUniversitas Ludwig-MaximiliansDikenal atasPrinsip eksklusi Pauli Regularisasi Pauli-Villars Matriks Pauli Efek Pauli Persamaan Pauli Kelompok Pauli Koin 'bahkan t...

Longest form of cricket This article is about the format for men's international cricket. For the women's format, see Women's Test cricket. Test CricketA Test match between South Africa and England in January 2007. The two men wearing black trousers are the umpires. Test cricket is played in traditional white clothes and usually with a red ball – a pink ball in full 1 day/night TestsHighest governing bodyICCCharacteristicsTeam membersFull membersMixed-sexNoTypeCricket formatGlossaryBat...

Parish in County Cork, Ireland This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2021) (Learn how and when to remove this template message) Parish in Munster, IrelandMourne Abbey Mainstir na MónaParishMourne AbbeyMourne AbbeyLocation in IrelandCoordinates: 52°08′N 8°39′W / 52.133°N 8.650°W / 52.133; -8.650CountryIrelandProv...

Эта статья или раздел нуждается в переработке.Пожалуйста, улучшите статью в соответствии с правилами написания статей. Мой шумный домангл. The Loud House Жанры комедийныйМультсериал Техники анимации компьютерная рисованная анимация (1—3 сезоны)flash-анимация (с 4 сезона) Созд�...

Mathematical transform which converts signals from the time domain to the frequency domain Not to be confused with Fisher z-transformation. In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain (the z-domain or z-plane) representation.[1][2] It can be considered a discrete-time equivalent of the Laplace transform (the s-domain or s-plane).[3] This sim...

Questa voce o sezione sull'argomento siti archeologici della Francia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. primeStato Francia RegioneAlvernia-Rodano-Alpi Dipartimento Ardèche ArrondissementLargentière CantoneVallon-Pont-d'Arc ComuneVallon-Pont-d'Arc Altitudine185 m s.l.m. Lunghezza511 m Data scoperta1994 Coordinate44°23�...

For other uses, see Dauphine. Historical region and former province of France Place in FranceDauphiné Daufinat / Dalfinat (Occitan)Dôfenât / Darfenât (Arpitan)Delphinatus Viennensis (Latin) FlagCoat of armsCountryFranceTime zoneCET The Dauphiné (UK: /ˈdoʊfɪneɪ, ˈdɔː-/, US: /ˌdoʊfiːˈneɪ/ French: [dofi'ne])[1][2] is a former province in southeastern France, whose area roughly corresponded to that of the present departments of Isère, Drôm...

Italian cycling team S.C. Michela Fanini RoxTeam informationUCI codeMICRegisteredItalyFounded1999 (1999)Disbanded2018Discipline(s)RoadStatusUCI Women's TeamBicyclesLombardoWebsiteTeam home pageTeam name history1999–20102011–2018SC Michela Fanini Record RoxS.C. Michela Fanini Rox S.C. Michela Fanini Rox (UCI team code: MIC) was a professional cycling team based in Italy, which competes in elite road bicycle racing events such as the UCI Women's Road World Cup and elite road races. Tea...

Symbol of Christianity ✝ redirects here. For the similar typographical symbol, see Dagger (mark). A crux immissa or Latin cross A Latin cross or crux immissa is a type of cross in which the vertical beam sticks above the crossbeam,[1] giving the cross four arms. Typically the two horizontal and upper vertical arm are the same length, although sometimes the vertical is shorter, however the lower vertical arm is always much longer than any other arm.[2] If displayed upside dow...

National Assembly Assemblée nationaleTypeTypeLower house HistoryFounded1962LeadershipPresidentGelase Ndabirabe[1] since 7 August 2020 StructureSeats100 directly elected, additional members co-opted to meet constitutional requirements[2]Political groups CNDD-FDD: 86 seats CNL: 32 seats UPRONA: 2 seats Twa: 3 seatsLength of term5 yearsElectionsVoting systemParty list proportional representationLast election20 May 2020Meeting placeK...

President of South Korea from 1948 to 1960 This article is about the first president of South Korea. For the Presbyterian minister, see Syngman Rhee (clergyman). In this Korean name, the family name is Rhee. Syngman Rhee 이승만 李承晩 Official portrait, 19481st President of South KoreaIn office24 July 1948 – 26 April 1960Prime Minister See list Lee Beom-seok Shin Song-mo (acting) Chang Myon Yi Yun-yong (acting) Chang Taek-sang Baek Du-jin Byeon Yeong-tae Vice President Yi...

American mass murderer (1952–1995) Bernard BolenderBolender's mugshotBorn(1952-09-01)September 1, 1952United StatesDiedJuly 18, 1995(1995-07-18) (aged 42)Florida State Prison, Raiford, Florida, U.S.Cause of deathExecution by electrocutionSpouseJoyce Bolender[1]Conviction(s)First degree murder (4 counts)Criminal penaltyDeathDetailsVictims4DateJanuary 8, 1980CountryUnited StatesState(s)Florida Bernard Bolender (September 1, 1952 – July 18, 1995)[2][3][...

Cartographer George PhilipBorn1800Huntly, AberdeenshireDied(1882-10-03)3 October 1882Bickley, KentOccupation(s)Cartographer and map publisherYears active1834–1882 George Philip (1800–1882) was a Scottish cartographer, map publisher and founder of the publishing house George Philip & Son Ltd. Family George Philip was born in Huntly, Aberdeenshire, to a staunchly Calvinist family. In 1819 George travelled to Liverpool where his brother Robert, who was a nonconformist minister, live...























![{\displaystyle DT=5\cdot log_{10}{[(BW\cdot d)/(2\cdot RC)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae2a6a287689bd1b4b98a0c0c4a319f493f08eb0)















