Numero di Strahler
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Star Wars: The Clone Wars Título Star Wars: La Guerra de los ClonesFicha técnicaDirección Dave FiloniProducción Catherine WinderGuion Henry GilroySteven MelchingScott MurphyBasada en Star Wars de George LucasMúsica Kevin KinerzTemas de: John WilliamsMontaje Jason TuckerProtagonistas Matt LanterAshley EcksteinJames Arnold TaylorTom KaneDee Bradley BakerChristopher LeeSamuel L. JacksonAnthony Daniels Ver todos los créditos (IMDb)Datos y cifrasPaís Estados UnidosAño 2008Género Animació...

Гроднa / Hrodna Гроднo / Grodno LambangNegaraSubdivisi BelarusHrodna VoblastDidirikan1128 (1127)Pemerintahan • MayorBarys KaziałkoŭPopulasi (2008) • Total349.700Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST)Kode area telepon+375-15License plate4Situs webwww.region.grodno.by Hrodna Hrodna[1] (bahasa Belarus: Гродна, bahasa Rusia: Гродно) ialah sebuah kota di Belarus, ibu kota Voblast Hrodna dan Raion Hrodna. S...

Suburb of Sydney, New South Wales, AustraliaFive DockSydney, New South WalesOld bank building on Great North Road, Five DockMapFive DockCoordinates33°51′54″S 151°07′43″E / 33.86512°S 151.12856°E / -33.86512; 151.12856Population9,356 (2016 census)[1] • Density3,819/km2 (9,891/sq mi)Established1794[citation needed]Postcode(s)2046Elevation22 m (72 ft)Area2.45 km2 (0.9 sq mi)Location10 km (6&#...

FEMA / EPA Tim Bahan Berbahaya menghilangkan bahaya yang tersisa setelah Badai Katrina, 2005. Kesehatan lingkungan merupakan cabang dari ilmu kesehatan masyarakat yang mencakup semua aspek alam dan lingkungan yang mempengaruhi kesehatan manusia. Kesehatan lingkungan berfokus pada kealami dan penciptaan lingkungan yang memberikan keuntungan pada manusia. Sub disiplin dari kesehatan lingkungan antara lain ilmu lingkungan, kesehatan dan keselamatan kerja, toksikologi dan epidemiologi. Istilah la...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...
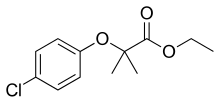
Chemical compound ClofibrateClinical dataAHFS/Drugs.comMicromedex Detailed Consumer InformationPregnancycategory AU: B1 Routes ofadministrationBy mouthATC codeC10AB01 (WHO) Legal statusLegal status US: Discontinued Pharmacokinetic dataProtein bindingVariable, 92–97% at therapeutic concentrationsMetabolismHydrolyzed to clofibric acid; hepatic glucuronidationElimination half-lifeHighly variable; average 18–22 hours. Prolonged in renal failureExcretionRenal, 95 to 9...

Weatherproof, sleeveless overcoat This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Inverness cape – news · newspapers · books · scholar · JSTOR (December 2016) (Learn how and when to remove this message) The formal form with lapels, 1901Formal coat without lapels, 1900Fashion plates of Inverness capes The Inv...

Mansion in Manhattan, New York Not to be confused with the Edward S. Harkness House, also called the Harkness Mansion. The Nathaniel L. McCready House, also known as the Harkness Mansion, is a mansion at 4 East 75th Street on the Upper East Side of New York City. Completed in 1896 for Nathaniel L’Hommediue McCready Jr., during the twentieth century it was occupied by Thomas J. Watson, Rebekah Harkness, whose name became associated with the building when she used it as the offices of the Har...

Portrait of Johann Burchard Freystein Johann Burchard Freystein (18 April 1671 – 1 April 1718) was a German lawyer and hymn writer. Life Freystein was born in Weissenfels, the son of Samuel Adam Freystein, vice-chancellor of Duke August of Saxony, inspector of the Gymnasium of Weissenfels. Johann Burchard Freyenstein studied at the University of Leipzig in law, mathematics, philosophy and architecture. He spent some time in Berlin and Halle. In 1695 he achieved his doctorate in law at the U...

Cricket stadium Dehradun, Uttarakhand, India This article is about a Cricket stadium in Dehradun. For Cricket stadium located in Hyderabad, see Rajiv Gandhi International Cricket Stadium. For Other stadium with Rajiv Gandhi name, see Rajiv Gandhi Stadium.Rajiv Gandhi International Cricket Stadium• Dehradun international cricket stadium • Dehradun Cricket StadiumThe Rajiv Gandhi International Cricket Stadium DehradunGround informationLocationDehradun, Uttarakhand, IndiaCoordinates30°17′...

Acis and Galatea on the Steble Fountain The city of Liverpool has a greater number of public sculptures than any other location in the United Kingdom aside from Westminster.[1] Early examples include works by George Frampton, Goscombe John, Thomas Thornycroft, Charles Bell Birch, Richard Westmacott, Francis Chantrey, John Gibson, Thomas Brock and F.W. Pomeroy, while Barbara Hepworth, Jacob Epstein, Mitzi Cunliffe and Elisabeth Frink provide some of the modern offerings. More recently...

Edotreotide Names IUPAC name 2-[4-[2-[[(2R)-1-[[(4R,7S,10S,13R,16S,19R)-10-(4-aminobutyl)-4-[[(2R,3R)-1,3-dihydroxybutan-2-yl]carbamoyl]-7-[(1R)-1-hydroxyethyl]-16-[(4-hydroxyphenyl)methyl]-13-(1H-indol-3-ylmethyl)-6,9,12,15,18-pentaoxo-1,2-dithia-5,8,11,14,17-pentazacycloicos-19-yl]amino]-1-oxo-3-phenylpropan-2-yl]amino]-2-oxoethyl]-7,10-bis(carboxymethyl)-1,4,7,10-tetrazacyclododec-1-yl]acetic acid Identifiers CAS Number 204318-14-9 N 3D model (JSmol) Interactive image ChemSpider 1396...

American economist Anne KruegerActing Managing Director of the International Monetary FundIn officeMarch 4, 2004 – June 7, 2004Preceded byHorst KöhlerSucceeded byRodrigo RatoFirst Deputy Managing Director of the International Monetary FundIn officeSeptember 1, 2001 – August 31, 2006Preceded byStanley FischerSucceeded byJohn LipskyChief Economist of the World BankIn office1982–1986PresidentAlden W. ClausenPreceded byHollis ChenerySucceeded byStanley Fischer Personal de...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2019) نظام القصف المداري الجزئي نظام القصف المداري الجزئي هو عبارة عن نظام لإيصال الأسلحة النووية تم تطويره في الستينيات من قبل الاتحاد السوفيتي.[1] نبذة هو أح�...

В Википедии есть статьи о других людях с такой фамилией, см. Куприн. Александр Васильевич Куприн Дата рождения 10 (22) марта 1880(1880-03-22) Место рождения Борисоглебск, Воронежская губерния, Российская империя Дата смерти 18 марта 1960(1960-03-18) (79 лет) Место смерти Москва, СССР Гражд�...

Pour les articles homonymes, voir Comté de Frederick. Cet article est une ébauche concernant le Maryland. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Comté de Frederick(Frederick County) Sceau du comté. Drapeau du comté. Centre-ville de Frederick en juin 2014 Administration Pays États-Unis État Maryland Chef-lieu Frederick Fondation 1748 Démographie Population 271 717 hab. (2020) Densité 1...

Marriott International Création 8 octobre 1993[1] Fondateurs J. Willard Marriott Forme juridique Société du Delaware (d) Action NASDAQ (MAR) Siège social Bethesda États-Unis Activité Hôtellerie-restauration et industrie du tourisme (d) Produits Hôtel, domaine touristique et franchise Filiales Delta Hotels (en) (depuis le 1er avril 2015)[2],[3]Westin Hotels & Resorts (depuis 2016)Starwood Hotels & Resorts WorldwideSheraton Hotels & ResortsResidence Inn by Marriott (en...

Referendum abrogativi in Italia del 1993Stato Italia Data18, 19 aprile TipoReferendum abrogativo Competenze USL Sì 82,57% No 17,43% Affluenza76,85% Stupefacenti e sostanze psicotrope Sì 55,36% No 44,64% Affluenza76,98% Finanziamento pubblico dei partiti Sì 90,25% No 9,75% Affluenza76,95% Casse di risparmio e Monti di pietà Sì 89,80% No 10,20% Affluenza76,87% Soppressione d...

Philosophical movement Part of a series onThomas Aquinas Thomism Scholasticism Apophatic theology Aseity Divine simplicity Quinque viae Beatific vision Actus purus Actus essendi Primum Movens Sacraments Correspondence theory Hylomorphism Substance theory (ousia) Substantial form Quiddity (essence / accident nature) Peripatetic axiom Principle of double effect Aristotelian ethics Cardinal / Theological Natural law Determinatio Just war Just price Concupiscence Intri...

Ecclesiastical province of the Church of England This article is about the ecclesiastical province in England. For the former civil province in New Zealand, see Canterbury Province. For the current administrative region in New Zealand, see Canterbury Region. For other uses, see Canterbury (disambiguation). Province of CanterburyChurchChurch of EnglandMetropolitan bishopArchbishop of CanterburyCathedralCanterbury CathedralDioceses30 The Province of Canterbury, or less formally the Southern Pro...
