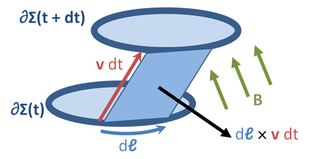
Legge di Faraday
|
Read other articles:

—— Permukiman di Uni Emirat Arab —— Al Butinالبطين Negara Uni Emirat Arab Emirat Dubai Kota Dubai Statistik permukiman Luas 0.07 km² Jumlah penduduk 2,364[1] (2000) Kepadatan penduduk 33,771/km² Permukiman sekitarnya Al Ras, Al Sabkha, Al Dhagaya, Naif Koordinat 25°16′07″N 55°17′54″E / 25.26861°N 55.29833°E / 25.26861; 55.29833 Al Buteen (Arab: البطينcode: ar is deprecated ) merupakan sebuah wilayah di Dubai, U...

Disambiguazione – Se stai cercando altri significati, vedi Paraguay (disambigua). Paraguay (dettagli) (dettagli) (ES) Paz y Justicia(GN) Py'aguapy ha Tekojoja(IT) Pace e Giustizia Paraguay - Localizzazione Dati amministrativiNome completoRepubblica del Paraguay Nome ufficiale(ES) República del Paraguay(GN) Paraguái Tavakuairetã Lingue ufficialiSpagnoloGuaranì Capitale Asunción (569.775 ab. / 2020) PoliticaForma di governoRepubblica presidenziale PresidenteSantiago...

Kensington St Mary Abbots Church, dilihat dari Church St, sebelum persimpangan Kensington High Street Population 64,681 [1](sensus 2011) Ref. grid OS TQ255795 Borough London County seremonial Greater London Wilayah London Negara konstituen Inggris Negara berdaulat Britania Raya Kota pos LONDON Distrik kode pos SW5, SW7 Distrik kode pos W8, W14 Kode telepon 020 Polisi Metropolitan Pemadam kebakaran London Ambulans London Parlemen&...

Kimbanseke, Kinshasa. Kimbanseke merupakan sebuah distrik di tenggara Kinshasa, ibu kota Republik Demokratik Kongo. Pemukiman di wilayah berbukit ini masih baru. Wikimedia Commons memiliki media mengenai Category:Kimbanseke (Kinshasa). lbsKomune di provinsi-kota KinshasaBandalungwa · Barumbu · Bumbu · La Gombe · Kalamu · Kasa-Vubu · Kimbanseke · Kinshasa (komune) · Kintambo · Kisenso · ...
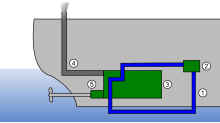
Sistem pendinginan dalam mesin kendaraan adalah suatu sistem yang berfungsi untuk menjaga supaya temperatur mesin dalam kondisi yang ideal. Mesin pembakaran dalam (maupun luar) melakukan proses pembakaran untuk menghasilkan energi dan dengan mekanisme mesin diubah menjadi tenaga gerak. Mesin bukan instrumen dengan efisiensi sempurna, panas hasil pembakaran tidak semuanya terkonversi menjadi energi, sebagian terbuang melalui saluran pembuangan dan sebagian terserap oleh material disekitar ruan...

Monument and marker for Teodoro R. Yangco in San Antonio, Zambales This list of historical markers installed by the National Historical Commission of the Philippines (NHCP) in Central Luzon (Region III) is an annotated list of people, places, or events in the region that have been commemorated by cast-iron plaques issued by the said commission. The plaques themselves are permanent signs installed in publicly visible locations on buildings, monuments, or in special locations. While many Cultu...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

1806 battle during the War of the Third Coalition Battle of Campo TenesePart of the War of the Third CoalitionCampotenese is located in the Morano Calabro municipality. The photo of Morano Calabro shows nearby mountainous terrain.Date9 March 1806LocationNorthwest of Morano Calabro, ItalyResult French victoryBelligerents France Polish Legions Switzerland Kingdom of Naples Kingdom of SicilyCommanders and leaders Jean Reynier Roger de DamasStrength 10,000 14,000Casualties and lo...

Gahwié got’iné, a Sahtú (North Slavey) people of Canada Indigenous people in northern Canada PeopleDeneCountryDenendeh For the Diné people native to the Southwestern US, see Navajo. For other uses, see Dene (disambiguation). Indigenous peoplesin Canada First Nations Inuit Métis History Timeline Paleo-Indians Pre-colonization Genetics Residential schools gravesites Indian hospitals Conflicts First Nations Inuit Truth and Reconciliation Commission Politics Indigenous law British Columbia...

American photographer (1911–2006) For the Canadian sculptor and political figure, see Joe Rosenthal (sculptor). For the British war camera operator, see Joseph Rosenthal (camera operator). For the Hebrew writer, see Yosef Rosenthal. For the German rabbi, see Joseph von Maier. Joe RosenthalRosenthal in 1990BornJoseph John Rosenthal(1911-10-09)October 9, 1911Washington, D.C., U.S.DiedAugust 20, 2006(2006-08-20) (aged 94)Novato, California, U.S.OccupationsPhotographerreporterKnown fo...

Michael OlindoMichael pada tahun 2021LahirMichael James Olindo15 Maret 2001 (umur 23)Jakarta, IndonesiaPekerjaanPemeranTahun aktif2015—sekarangTinggi175 cm (5 ft 9 in)[1] Michael James Olindo (lahir 15 Maret 2001) adalah aktor dan mantan pebasket berkebangsaan Indonesia. Michael memulai karier sebagai atlet dengan bergabung dalam klub basket Victoria Basketball Club, kemudian di tahun 2017 Michael terpilih untuk masuk dalam Tim nasional bola basket Indonesi...

1993 live album by Tangerine Dream220 Volt LiveOriginal release coverLive album by Tangerine DreamReleasedJune 4, 1993Recordedvarious dates in October and November 1992GenreElectronic rock, new-age, synthpopLength72:40LabelMiramarProducerEdgar FroeseTangerine Dream chronology Deadly Care(1992) 220 Volt Live(1993) Turn of the Tides(1994) Professional ratingsReview scoresSourceRatingAllMusic[1] 220 Volt Live is the forty-eighth release and seventh live album by Tangerine Dream. ...

Company AECL redirects here. For other uses, see AECL (disambiguation). Atomic Energy of Canada LimitedCompany typeCrown corporationIndustryNuclear power researchFounded1952HeadquartersChalk River, Ontario, CanadaKey peopleFred Dermarkar, President and CEORevenue CA$900 million (2017)[citation needed]Total assets CA$1.071 billion (2017)[citation needed]OwnerGovernment of CanadaNumber of employees3500 worldwideSubsidiariesCanadian Nuclear LaboratoriesWebsitewww.aecl.c...

Italian painter Self-portrait (date unknown) Odoardo Borrani (22 August 1833 – 14 September 1905) was an Italian painter associated with the Macchiaioli group. Biography He was born in Pisa. The Borrani family moved to Florence, where Odoardo enrolled at the Academy of Fine Arts in 1853. There, he studied under Gaetano Bianchi [it], Giuseppe Bezzuoli, and Enrico Pollastrini. However, he became independent of the academic styles. Cucitrici di camicie rosse (Sewing red shirts for...

Pulau KakabanLokasi Pulau KakabanGeografiLokasiAsia TenggaraKoordinat2°09′N 118°32′E / 2.150°N 118.533°E / 2.150; 118.533KepulauanKepulauan DerawanLuas7,742 km2PemerintahanNegara IndonesiaProvinsi Kalimantan TimurKependudukanPendudukTidak berpenghuni Pulau Kakaban mempunyai luas 774,2 hektar dan terletak di Kepulauan Derawan, Kecamatan Derawan, Kabupaten Berau, Kalimantan Timur. Pulau ini merupakan atol atau batu karang melingkar dan memiliki lag...

American baseball player (born 1997) Baseball player Luken BakerBaker with the Palm Beach Cardinals in 2019St. Louis Cardinals – No. 26First basemanBorn: (1997-03-10) March 10, 1997 (age 27)Spring, Texas, U.S.Bats: RightThrows: RightMLB debutJune 4, 2023, for the St. Louis CardinalsMLB statistics (through 2023 season)Batting average.209Home runs2Runs batted in10 Teams St. Louis Cardinals (2023–present) Luken Grosvenor Baker (born March 10, 1997) is an American professi...

Хип-хоп Направление популярная музыка Истоки фанкдискоэлектронная музыкадабритм-энд-блюзреггидэнсхоллджаз[1]чтение нараспев[англ.]исполнение поэзииустная поэзияозначиваниедюжины[англ.]гриотыскэтразговорный блюз Время и место возникновения Начало 1970-х, Бронкс, Н...

Cet article est une ébauche concernant le génie mécanique et la physique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Lignes de tension dans un rapporteur en plastique vu sous une lumière polarisée grâce à la photoélasticité. En mécanique des milieux continus, et en résistance des matériaux en règle générale, la contrainte mécanique (autrefois appelée tension[1] ou « fatigue élastique...

For other people named Charles Clarke, see Charles Clarke (disambiguation). British Labour politician This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Charles Clarke – news · newspapers · books · schol...

Business intelligence suite IBM Cognos AnalyticsDeveloper(s)IBMStable release12.0.0 / June 2023; 1 year ago (2023-06) Operating systemMicrosoft Windows, Linux, UNIXPlatformCross-platform softwareAvailable inMulti-lingualTypeBusiness intelligenceData visualizationAnalyticsLicenseProprietaryWebsitewww.ibm.com/products/cognos-analytics IBM Cognos Analytics with Watson (aka Cognos Analytics, and formerly known as IBM Cognos Business Intelligence) is a web-based integrated b...