Gruppo di Coxeter
|
Read other articles:

Blanche PaysonPayson pada sekitar tahun 1915LahirMary Elizabeth Bush(1881-09-20)20 September 1881Santa Barbara, California, Amerika SerikatMeninggal4 Juli 1964(1964-07-04) (umur 82)Hollywood, California, Amerika SerikatTahun aktif1916–1946 Blanche Payson (nama lahir Mary Elizabeth Bush, 20 September 1881 – 4 Juli 1964) adalah seorang pemeran film perempuan asal Amerika Serikat. Ia tampil dalam sekitar 160 film antara 1916 dan 1946. Filmografi pilihan Wife and Auto...

Komisi inti dari Kongres: 1. Father Gjergj Fishta 2. Mid'hat Fashëri 3. Luigj Gurakuqi 4. Gjergj Qiriazi 5. Ndre Mjedja 6. G. Cilka 7. Taqi Buda 8. Shahin Kolonja 9. Sotir Peçi 10. Bajo Topulli 11. Nyzhet Vrioni Foto oleh Kel Kodheli. Kongres Monastir (bahasa Albania: Kongresi i Manastirit) adalah sebuah lokakarya yang diselenggarakan di kota Monastir dari tanggal 14 sampai 22 November 1908, dengan tujuan untuk menstandarisasi Alfabet Albania. 22 November sekarang dirayakan di Albania s...

Bustan Urip Bustan Urip adalah seorang guru, birokrat dan politikus Indonesia. Ia lahir di Lubukrukam, Baturaja pada tanggal 12 Mei 1899. Ia menimba ilmu di Kweekschool Bukittinggi dan Opsichter S.S. Ia adalah anggota partai Persatuan Indonesia Raya (PIR). Setelah tamat Kweekschool, pada tahun 1917, ia menjadi guru HIS di Payakumbuh, Sumatera Barat. Dari 1935 sampai 1939, ia pernah duduk sebagai anggota Volksraad. Kemudian, dari 1919 sampai 1945, ia menjabat sebagai Opzichter S.S. untuk selan...

DiernaLocation within RomaniaAlternative name(s)Tierna [1]Known also asCastra of OrșovaFounded during the reign ofTrajanPlace in the Roman worldProvinceDaciaAdministrative unitDacia ApulensisAdministrative unitDacia SuperiorDirectly connected toPraetoriumStructure— Stone structure —Size and area64 m × 54 m (0.35 [2] ha) Stationed military units— Legions — vexill. V Macedonica[3] vexill. XXII Primigenia vexill. XIII Gemina[3] — Cohorts —I Brittonum...

Elezioni generali in Spagna del 2000 Stato Spagna Data 12 marzo Legislatura VII Assemblee Congresso dei Deputati, Senato di Spagna Affluenza 68,71% ( 8,67%) Leader José María Aznar Joaquín Almunia Artur Mas Liste PP PSOE CU Congresso dei Deputati Voti 10.321.17844,52% 7.918.75234,16% 970 4214,19% Seggi 183 / 350 125 / 350 15 / 350 Senato di Spagna Seggi 127 / 208 53 / 208 8 / 208 Distribuzione del voto per provincia (Congresso) Governi Aznar II 1996 2004 Le elezioni generali in Spag...

North Carolina's 1st congressional district special election, 2004 ← 2002 July 20, 2004 (2004-07-20) November 2004 → Nominee G. K. Butterfield Greg Dority Party Democratic Republican Popular vote 48,567 18,491 Percentage 71.15% 27.09% County resultsButterfield: 50–60% 60–70% 70–80% 80–90% Representative before electio...

Part of a series onAnthropology OutlineHistory Types Archaeological Biological Cultural Linguistic Social Archaeological Aerial Aviation Battlefield Biblical Bioarchaeological Environmental Ethnoarchaeological Experiential Feminist Forensic Maritime Paleoethnobotanical Zooarchaeological Biological Anthrozoological Biocultural Evolutionary Forensic Molecular Neurological Nutritional Paleoanthropological Primatological SocialCultural Applied Art Cognitive Cyborg Development Digital Ecological E...

American mystery drama soap opera television series MistressesGenre Drama Mystery Soap opera Based onMistressesby Lowri Glain and S. J. ClarksonDeveloped byK. J. SteinbergStarring Alyssa Milano Yunjin Kim Rochelle Aytes Jes Macallan Jason George Brett Tucker Erik Stocklin Rob Mayes Jennifer Esposito Tabrett Bethell ComposerDanny LuxCountry of originUnited StatesOriginal languageEnglishNo. of seasons4No. of episodes52 (list of episodes)ProductionExecutive producers Rina Mimoun Douglas Rae Gran...

Martian meteorite Mackinac Island meteorite TypeIronParent bodyUnknownCompositionNickel, iron, Kamacite, taenite[1][2]Weathering gradeLarge-scale, cavernous weathering[2]CountryMarsRegionMeridiani PlanumCoordinates02°07′02″S 05°31′22.43″W / 2.11722°S 5.5228972°W / -2.11722; -5.5228972[3]Observed fallNoFall datePossibly late NoachianFound date2009-10-13[4]Strewn fieldPossibly[5] Related media on Wikimedia Commo...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Cette page concerne l'année 1828 (MDCCCXXVIII en chiffres romains) du calendrier grégorien. Chronologies 20 avril : René Caillé à Tombouctou.Données clés 1825 1826 1827 1828 1829 1830 1831Décennies :1790 1800 1810 1820 1830 1840 1850Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun...

NGC 4195 الكوكبة الدب الأكبر[1] رمز الفهرس NGC 4195 (الفهرس العام الجديد)2MASX J12141805+5936550 (Two Micron All-Sky Survey, Extended source catalogue)UGC 7244 (فهرس أوبسالا العام)PGC 39082 (فهرس المجرات الرئيسية)MCG+10-18-010 (فهرس المجرات الموروفولوجي)Z 292-83 (فهرس المجرات وعناقيد المجرات)Z 293-4 (فهرس المجرات وعناقيد المج...
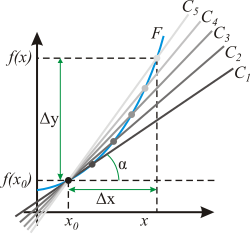
График функции (чёрная кривая) и касательная прямая (красная прямая) Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка. Содержание 1 Строгое определение 2 Замечание 3 Касательная как предельное �...

River in Western Asia Shatt al-ArabShatt al-Arab pictured near Basra, IraqDrainage basin and two major tributariesLocationCountryIraq, Iran, Kuwait[1][2]Physical characteristicsSourceEuphrates • elevation4 m (13 ft) 2nd sourceTigris • elevation4 m (13 ft) Mouth • locationPersian Gulf • coordinates30°24′15.59″N 48°09′3.60″E / 30.4043306°N 48.1510000°E...

Sea piracy in 2022 2022 in piracy resulted in 115 reports of maritime piracy and armed robbery against ships to the International Maritime Bureau.[1] 288 acts of global piracy and robbery were recorded by the MICA Centre.[2] Piracy had substantially increased in the Gulf of Guinea; the year began with five incidents each month, through March, in the Gulf, where acts of piracy had become heightened during 2015 through 2020, while, overall, piracy incidents declined globally. ...

Mercedes O. CubriaLt. Col. Mercedes O. CubriaThe first Cuban-born female officer in the U.S. ArmyNickname(s)TiaBorn(1903-04-15)April 15, 1903Guantanamo, CubaDiedOctober 14, 1980(1980-10-14) (aged 77)Miami, FloridaAllegiance United States of AmericaService/branch United States ArmyYears of service1943-1973Rank Lieutenant ColonelBattles/warsWorld War IIKorean WarCold WarAwardsLegion of Merit (2)Bronze Star Medal Lieutenant Colonel Mercedes Olympia Cubria[1] (April 15, 190...

Untuk pesawat udara, lihat Elang Hitam. Elang hitam Status konservasi Risiko Rendah Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Accipitriformes Famili: Accipitridae Genus: IctinaetusBlyth, 1843 Spesies: I. malayensis Nama binomial Ictinaetus malayensisTemminck, 1822 Sinonim Neopus malayensis Ictinaetus malayensis Aquila pernigra Elang hitam (Ictinaetus malayensis) adalah sejenis burung pemangsa dari suku Accipitridae, dan satu-satunya anggota genus Ictinaetus....

Ankur NayyarAnkur Nayyar dalam peluncuran Sekolah Pertunjukan Seni ITALahir27 Mei 1977 (umur 47)Pathankot, Punjab, IndiaTempat tinggalMumbai, Maharashtra, IndiaKebangsaanIndianPekerjaanaktorTahun aktif2001–sekarangSuami/istriRikita ManujaAnak1 Ankur Nayyar (lahir 27 Mei 1977) adalah aktor televisi dan film India. Dia telah bekerja di banyak acara seperti Kasautii Zindagii Kay, Kashmeer dan Jeet. Dia dikenal karena memainkan peran utama Samman Chaudhary di Sahara One acara Ghar Ek...

Russian Research team All-Russian Scientific Research Institute Of Technical PhysicsCompany typeFederal State Unitary EnterpriseFounded1955HeadquartersSnezhinsk, RussiaParentRosatomWebsitevniitf.ru All-Russian Scientific Research Institute Of Technical Physics (VNIITF) (Russian: Всероссийский научно-исследовательский институт технической физики) is a research institute based in Snezhinsk, Russia. It was previously also known as NII-...

Children's television channel in Scandinavia This article is about a version of Disney Channel broadcast to Nordic countries. For other international versions, see Disney Branded Television. Television channel Disney Channel (Scandinavia)CountryUnited KingdomBroadcast area Denmark Faroe Islands Finland Iceland Norway Sweden Headquarters3 Queen Caroline Street, Hammersmith, London W6 9PE, United KingdomProgrammingLanguage(s) Swedish Norwegian Danish English Finnish (subtitles for most TV shows...
























