Gradino di potenziale
|
Read other articles:

DaisyVersi digital Jepang dan TiongkokSingel oleh Pentagondari album WE:THDirilis12 Oktober 2020 (2020-10-12)StudioCube StudioGenreK-popalternative rockDurasi3:09Label Cube Universal Music Pencipta Lee Hoe-taek Jung Woo-seok Lee Kyochang Produser Hui Wooseok 네이슨 (NATHAN) Kronologi singel Pentagon Basquiat (2020) Daisy (2020) Eternal Flame (2020) Music videoDaisy di YouTube Daisy (Hangul: 데이지; RR: Deiji) adalah lagu yang direkam oleh grup vokal pria Korea Selatan Pentagon, dir...

Football leagueGerman football championship (Deutsche Fußballmeisterschaft)Founded1903Replaced byBundesliga(since 1963–64)CountryGermanyOther club(s) fromFree City of DanzigNumber of teams18Level on pyramidLevel 1Current championsBayern Munich (33rd title) (2022–23)Most championshipsBayern Munich (33 titles) The German football champions are the annual winners of the highest association football competition in Germany. History The history of the German football championship is complex a...

Brian Ray Skeet Ulrich (lahir 20 Januari 1968) merupakan seorang aktor berkebangsaan Amerika Serikat. Dia menjadi terkenal saat bermain di drama seperti Jericho. Dia dilahirkan di Lynchburg, Virginia. Dia berkarier di dunia film sejak tahun 1989. Filmografi Jericho (seri TV) … Jake Green Into the West (2005) (mini) Seri TV … Jethro Wheeler The Magic of Ordinary Days (2005) (TV) … Ray Singleton Miracles (TV series) (2003) TV Series … Paul Callan Chilly Dogs (2001) … Kevin Manley Soul...

Japanese manga series Tokyo YamimushiFirst tankōbon volume cover東京闇虫GenreCrime[1] MangaWritten byYūki HondaPublished byHakusenshaMagazineYoung AnimalDemographicSeinenOriginal runAugust 27, 2010 – January 11, 2013Volumes7 MangaTokyo Yamimushi -2nd Scenario- PandoraWritten byYūki HondaPublished byHakusenshaMagazineYoung AnimalDemographicSeinenOriginal runFebruary 22, 2013 – January 22, 2016Volumes8 Tokyo Yamimushi (東京闇虫) is a Japanese manga ser...

The Greater Košice District in the Kosice Region Hosťovce (Hungarian: Bódvavendégi) is a village and municipality in the Greater Košice District in the Kosice Region of eastern Slovakia. The village has a Hungarian population. History The village was first mentioned in historical records in 1360. From 1964 to 1990, together with the villages of Chorváty and Turnianska Nová Ves, Hosťovce was part of the village of Nová Bodva. Geography The village lies at an elevation of 171 meters an...

Medication AmilorideClinical dataTrade namesMidamor, othersOther namesMK-870AHFS/Drugs.comMonographPregnancycategory AU: C Routes ofadministrationBy mouthATC codeC03DB01 (WHO) Legal statusLegal status AU: S4 (Prescription only) UK: POM (Prescription only) US: ℞-only Pharmacokinetic dataBioavailabilityReadily absorbed, 15–25%Protein binding~23%MetabolismNilOnset of action2 hours (peak at 6–10 hours, duration ~24 hours)Elimination half-life6 to 9 hoursExcreti...

American neurologist, skeptic (b. 1964) Steven NovellaNovella in 2013BornSteven Paul Novella (1964-07-29) July 29, 1964 (age 59)Danbury, Connecticut, U.S.Alma materGeorgetown UniversityKnown for Editor of Science-Based Medicine Host of The Skeptics' Guide to the Universe podcast Scientific careerFieldsClinical neurologyInstitutionsYale School of Medicine Medical careerProfessionNeurologySub-specialtiesBotulinum therapy, ALS/myasthenia gravis and neuromuscular disorders, general...

André Onana Onana bersama Kamerun pada 2022Informasi pribadiNama lengkap André Onana[1]Tanggal lahir 2 April 1996 (umur 28)[2]Tempat lahir Nkol Ngok, Kamerun[2]Tinggi 1,90 m (6 ft 3 in)[3]Posisi bermain Penjaga GawangInformasi klubKlub saat ini Manchester UnitedNomor 23Karier junior2006–2010 Samuel Eto'o Academy2010–2015 BarcelonaKarier senior*Tahun Tim Tampil (Gol)2015–2016 Jong Ajax 39 (0)2016–2022 Ajax 148 (0)2022–2023 Inter ...

2008 book by Muhammad Mojlum Khan The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (June 2020) (Learn how and when to remove this message) The Muslim 100: The Lives, Thoughts and Achievements of the Most Influential Muslims in History AuthorMuhammad Mojlum KhanCover artistNasir CadirCountryUnited KingdomLanguageEnglishSubjectBiographical dictionaryGenreNon-fictionPublisherKu...
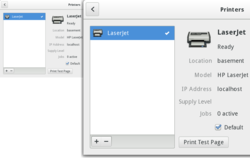
Computer display feature Resolution independence is where elements on a computer screen are rendered at sizes independent from the pixel grid, resulting in a graphical user interface that is displayed at a consistent physical size, regardless of the resolution of the screen.[1] Concept As early as 1978, the typesetting system TeX due to Donald Knuth introduced resolution independence into the world of computers. The intended view can be rendered beyond the atomic resolution without an...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Thiên hà Andromeda với M110 ở phía trên bên trái và M32 ở bên phải lõi. Thiên hà Andromeda (M31) có các thiên hà vệ tinh giống như Ngân Hà. Quỹ đạo M31 có ít nhất 13 thiên hà lùn: sáng nhất và lớn nhất là M110 có thể nhìn thấy bằng kính viễn vọng cơ bản. Sáng thứ hai và gần nhất với M31 là M32. Các thiên hà khác mờ hơn và hầu hết chỉ được phát hiện từ những năm 1970. Vào ngày 11 tháng 1 ...

Міністерство оборони України (Міноборони) Емблема Міністерства оборони та Прапор Міністерства оборони Будівля Міністерства оборони у КиєвіЗагальна інформаціяКраїна УкраїнаДата створення 24 серпня 1991Попередні відомства Міністерство оборони СРСР Народний комісарі...

Chemical compound TetrahydrocannabihexolIdentifiers IUPAC name (6aR,10aR)-3-hexyl-6,6,9-trimethyl-6a,7,8,10a-tetrahydrobenzo[c]chromen-1-ol CAS Number36482-24-3PubChem CID161906ChemSpider142196CompTox Dashboard (EPA)DTXSID90957796 Chemical and physical dataFormulaC22H32O2Molar mass328.496 g·mol−13D model (JSmol)Interactive image SMILES CCCCCCC1=CC(=C2[C@@H]3C=C(CC[C@H]3C(OC2=C1)(C)C)C)O InChI InChI=1S/C22H32O2/c1-5-6-7-8-9-16-13-19(23)21-17-12-15(2)10-11-18(17)22(3,4)24-20(21)14-16/h1...

Grand Prince of Kiev from 1113 to 1125 You can help expand this article with text translated from the corresponding article in French. (February 2014) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine...

Silver LakeSilver Lake at Nichols Beach, Madison, NHSilverLakeShow map of New HampshireSilverLakeShow map of the United StatesLocationCarroll County, New HampshireCoordinates43°51′57″N 71°10′24″W / 43.86583°N 71.17333°W / 43.86583; -71.17333Primary inflowsDeer RiverForrest BrookPrimary outflowsWest BranchBasin countriesUnited StatesMax. length2.6 mi (4.2 km)Max. width1.2 mi (1.9 km)Surface area969 acres (3.92 km2)Average depth4...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Manusia[1] Periode 0,35–0 PreЄ Є O S D C P T J K Pg N Pleistosen Tengah – Kini Homo sapiens Laki-laki (kiri) dan perempuan (kanan) dari Suku Akha di utara ThailandRekaman TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoPrimatesFamiliHominidaeGenusHomoSpesiesHomo sapiens Linnaeus, 1758 Tata namaSinonim takson Sinonim spesies[1] aethiopicusBory de St. Vincent, 1825 americanusBory de St. Vincent, 1825 arabicusBory de St. Vincent, 1825 aurignacensisKlaatsch & Haus...

Chief Justice of India Dhananjaya Y. ChandrachudChandrachud in January 202450th Chief Justice of IndiaIncumbentAssumed office 9 November 2022Appointed byPresident of IndiaPreceded byUday Umesh LalitJudge of the Supreme Court of IndiaIn office13 May 2016 – 8 November 2022Nominated byT. S. ThakurAppointed byPranab MukherjeeChief Justice of the Allahabad High CourtIn office31 October 2013 – 12 May 2016[1]Nominated byP. SathasivamAppointed byPranab MukherjeeJudge...

American businessman Bill RancicRancic in 2010BornWilliam Rancic (1971-05-16) May 16, 1971 (age 53)Chicago, Illinois, U.S.EducationLoyola University Chicago (BS)OccupationsEntrepreneurauthortelevision personalityYears active2004–presentSpouse Giuliana DePandi (m. 2007)Children1Websitewww.billrancic.com William Rancic (/ˈrænsɪk/; born May 16, 1971)[1] is an American entrepreneur who was the first candidate hired by The Trump Organization at...












































