Formule di Waring
|
Read other articles:

جزء من سلسلة مقالات عناليهودية التاريخ الخط الزمني الخروج زمن الملكية زمن السبي المحرقة إسرائيل تاريخ اليهودية التقويم العقائد الله أسماء الله يهوه إل) الوصايا العشر الشعب المختار الأنبياء مشيح نجمة داود النصوص التناخ التوراة الأسفار المقدسة قبالة هالاخاه التلمود شخصي�...

العلاقات الكورية الشمالية الكولومبية كوريا الشمالية كولومبيا كوريا الشمالية كولومبيا تعديل مصدري - تعديل العلاقات الكورية الشمالية الكولومبية هي العلاقات الثنائية التي تجمع بين كوريا الشمالية وكولومبيا.[1][2][3][4][5] مقارنة بين البلدي�...
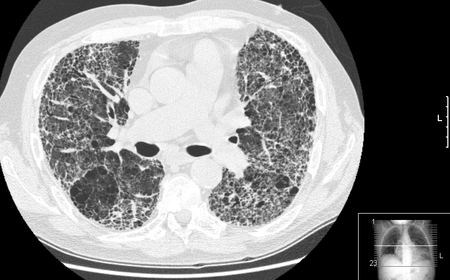
Penyakit Paru RestriktifInformasi umumNama lainDefek ventilasi restriktifSpesialisasiPulmonologiTipeTipe intrinsik dan ekstrinsikPenyebabMultifaktorAspek klinisGejala dan tandaNapas pendek, sesak napas, batukAwal munculUsia 20-40 tahunDurasiAkut, subakut, kronisDiagnosisFoto toraks, tes fungsi paru, HRCT, lavase bronkoalveolarPerawatanMedikamentosa, terapi oksigen, terapi ventilator, fisioterapi, transplantasi paruPengobatanKortikosteroid, azotioprin, kolkisin, nintedanib, pirfenidon.Prevalen...

Qiao Shi乔石Qiao Shi pada 1994 Ketua Komite Pendirian Kongres Rakyat Nasional ke-6Masa jabatan27 Maret 1993 – 15 Maret 1998 PendahuluWan LiPenggantiLi PengSeretaris Komisi Pusat untuk Inspeksi KedisiplinanMasa jabatanOktober 1987 – Oktober 1992 PendahuluChen Yun(sekretaris pertama)PenggantiWei JianxingANggota Komite Pendirian Politburo PKT ke-13, ke-14Masa jabatan2 November 1987 – 19 September 1997General SecretaryZhao ZiyangJiang ZeminSekretaris Komisi ...

Ezekiel JacksonJackson pada tahun 2012Nama lahirRycklon StephensLahir22 April 1978 (umur 45)[1]Linden, GuyanaAlma materUniversity at BuffaloPasanganJenn Stephens (m. 2004)Anak2Karier gulat profesionalNama ringBig Ryck[2]Big Ryck Hytz[1]Big RycklonBig ZekeEzekiel[1]Ezekiel Jackson[1]Ricky Atlas[1]RycklonRycklon Stephens[1]Tinggi6 ft 4 in (193 cm)[3]Berat309 pon (140 kg)&...

British politician (born 1946) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Robert Gascoyne-Cecil, 7th Marquess of Salisbury – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this template message) The Most HonourableThe Marquess of SalisburyKG KCVO PC DLLord Salisbury in 2013Chancellor of the Un...

العلاقات المارشالية الجيبوتية جزر مارشال جيبوتي جزر مارشال جيبوتي تعديل مصدري - تعديل العلاقات المارشالية الجيبوتية هي العلاقات الثنائية التي تجمع بين جزر مارشال وجيبوتي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين...

Kingdom of ThailandMinistry of FinanceกระทรวงการคลังKrasuang Kan KhlangThe Seal of the Bird of Paradise used as the Ministry's sealMinistry of FinanceMinistry overviewFormed14 April 1875; 148 years ago (1875-04-14)Preceding agenciesMinistry of TreasuryDepartment of TreasuryJurisdictionGovernment of ThailandHeadquartersPhaya Thai, BangkokAnnual budget242,948M baht (FY2019)Ministers responsibleSrettha Thavisin, Minister of FinancePrasong Poontaneat...

Flower BudAlbum mini karya GFriendDirilis27 Juli 2015 (2015-07-27)GenreK-pop, pop bubblegumDurasi19:41LabelSource MusicKT MusicKronologi GFriend Season of Glass(2015)Season of Glass2015 Flower Bud(2015) Snowflake(2016)Snowflake2016 Singel dalam album Flower Bud Me Gustas TuDirilis: 23 Juli 2015 Flower Bud adalah album mini kedua dari grup vokal wanita asal Korea Selatan GFriend. Album ini dirilis pada tanggal 23 Juli 2015 oleh Source Music, dengan singel utama Me Gustas Tu digunakan ...

Santa Maria Maddalena de' PazziVisione di santa Maria Maddalena de' Pazzi, dipinto di Pedro de Moya Religiosa NascitaFirenze, 2 aprile 1566 MorteFirenze, 25 maggio 1607 Venerata daChiesa cattolica Beatificazione8 maggio 1626 da papa Urbano VIII Canonizzazione22 aprile 1669 da papa Clemente IX Ricorrenza25 maggio Manuale Maria Maddalena de' Pazzi, al secolo Caterina Lucrezia (Firenze, 2 aprile 1566 – Firenze, 25 maggio 1607), è stata una religiosa carmelitana, proclamata santa da...
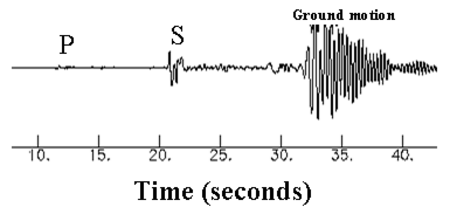
クルアーンのスーラについては「地震 (クルアーン)」をご覧ください。 ポータル 災害 地震(じしん、英: earthquake)は、以下の2つの意味で用いられる[1]。 地震学における定義: 地球表面を構成している岩盤(地殻)の内部で、固く密着している岩石同士が、断層と呼ばれる破壊面を境目にして、急激にずれ動くこと。これによって大きな地面の振動が生じ�...

Logo de Megaupload Adresse www.megaupload.com Slogan The leading online storage and file delivery service Commercial Oui Publicité Oui Type de site Site d'hébergement de fichiers en un clic Langue Multilingue (20 langues) Inscription Facultative Siège social Hong Kong Chine Propriétaire Megaupload Limited Créé par Kim Dotcom Lancement 21 mars 2005 Fermeture 19 janvier 2012 État actuel Fermé modifier Megaupload était un site web, créé en 2005 par Kim Dotcom et fer...

College Football Bowl Subdivision team; member of Atlantic Coast Conference Clemson Tigers football2024 Clemson Tigers football team First season1896; 128 years ago (1896)Athletic directorGraham NeffHead coachDabo Swinney 15th season, 170–40 (.810)StadiumMemorial Stadium(capacity: 82,000)FieldFrank Howard FieldYear built1942Field surfaceNatural GrassLocationClemson, South CarolinaNCAA divisionDivision I FBSConferenceAtlantic Coast ConferenceDivisionAtlanticPast conferences...

Численность населения республики по данным Росстата составляет 4 003 016[1] чел. (2024). Татарстан занимает 8-е место по численности населения среди субъектов Российской Федерации[2]. Плотность населения — 59,00 чел./км² (2024). Городское население — 76,72[3] % (20...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

В Википедии есть статьи о других людях с фамилией Кисслинг. Ребекка Кисслингангл. Rebecca Kiessling Дата рождения 22 июля 1969(1969-07-22) (54 года) Место рождения Мичиган, США Гражданство США Род деятельности Гражданский активист, пролайфер, правозащитник Сайт rebeccakiessling.com М...

رمزيرمز المثمن الأحمر لعملية التوقف، دون الحاجة إلى كلمة مكتوبة.معلومات عامةصنف فرعي من علامةصورة جزء من تدوين الاسم Symbols (بالإنجليزية) [1]symboles (بالفرنسية) [1] الأسباب symbolism (en) يدرسه علم العلامات تعديل - تعديل مصدري - تعديل ويكي بيانات الرمز (بالإنجليزية: Symbol) يعني ال�...

NGC 4672 الكوكبة قنطورس[1] رمز الفهرس NGC 4672 (الفهرس العام الجديد)MCG-07-26-041 (فهرس المجرات الموروفولوجي)IRAS 12435-4125 (IRAS)IRAS 12435-4126 (IRAS)PGC 43073 (فهرس المجرات الرئيسية)ESO 322-73 (European Southern Observatory Catalog)2MASX J12461573-4142214 (Two Micron All-Sky Survey, Extended source catalogue)6dFGS gJ124615.8-414222 (6dF Galaxy Survey)AGC 28788 (Arecibo General Catalog)AM...

الدوري السوفيتي الممتاز لكرة القدم 1989 تفاصيل الموسم الدوري السوفييتي الممتاز النسخة 53 البلد الاتحاد السوفيتي التاريخ بداية:11 مارس 1989 نهاية:27 أكتوبر 1989 المنظم الاتحاد السوفيتي لكرة القدم البطل سبارتاك موسكو مباريات ملعوبة 240 عدد المشاركين 16 ...

Dam in Seraikela Kharsawan district, JharkhandChandil DamChandil DamLocation in JharkhandShow map of JharkhandChandil Dam (India)Show map of IndiaCountryIndiaLocationSeraikela Kharsawan district, JharkhandCoordinates22°58′29″N 86°01′13″E / 22.9747°N 86.0203°E / 22.9747; 86.0203StatusFunctionalConstruction began1982–1993 (1982–1993)Dam and spillwaysImpoundsSubarnarekha RiverHeight56.5 m (185 ft).Length720.10 m (2,362.5 ft)Re...



























![{\displaystyle m=[1;n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b51e3f17749a9cd3ee2040dbd96d2dc7b0078620)
![{\displaystyle o=[1;n-2k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96566eb3df5964be55b29364408c5b206e5659ca)


![{\displaystyle a^{n}+b^{n}=(a+b)^{n}-\sum _{i=1}^{f_{1}}T_{i}a^{i}b^{i}[a^{n-2i}+b^{n-2i}]-f_{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a01c6242ebd66d418b5036f774aef741029a73)


![{\displaystyle {f_{1}}=[n/2-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04513b00f2eb7d55e3bd989ec6beb64e9fc1f0d)


