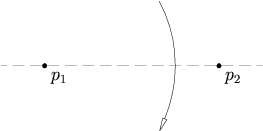
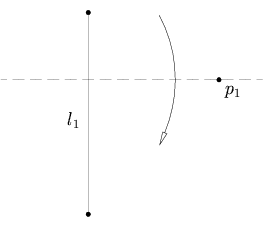
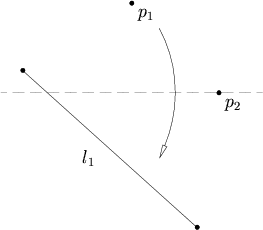
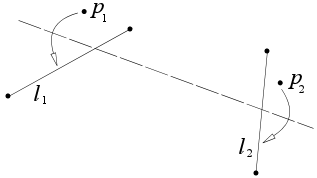
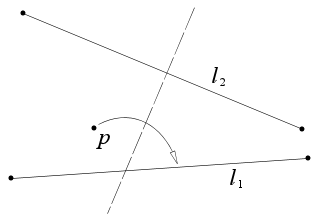
Assiomi di Huzita-Hatori
|
Read other articles:

Begonia listada TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladfabidsOrdoCucurbitalesFamiliBegoniaceaeGenusBegoniaSpesiesBegonia listada L.B.Sm. dan Wassh., 1981 lbs Begonia listada adalah spesies tumbuhan yang tergolong ke dalam famili Begoniaceae. Spesies ini juga merupakan bagian dari ordo Cucurbitales. Nama ilmiah spesies ini pertama kali diterbitkan oleh Lyman Bradford Smith dan Dieter Carl Wa...

American baseball player (1905-1972) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2019) (Learn how and when to remove this template message) Baseball player Danny MacFaydenPitcherBorn: (1905-06-10)June 10, 1905Truro, Massachusetts, U.S.Died: August 26, 1972(1972-08-26) (aged 67)Brunswick, Maine, U.S.Batted: Rig...

Hole in the back of the temporal bone Mastoid foramenLeft temporal bone. Inner surface. (Mastoid foramen labeled at bottom left.)Base of the skull. Upper surface. (Temporal bone is pink, and label for mastoid foramen is at left, second from the bottom.)DetailsPart oftemporal bone of skullSystemskeletalIdentifiersLatinforamen mastoideumTA98A02.1.06.008TA2649FMA53159Anatomical terms of bone[edit on Wikidata] The mastoid foramen is a hole in the posterior border of the temporal bone. It tran...

Calcium ascorbate Names IUPAC name Calcium (2R)-2-[(1S)-1,2-dihydroxyethyl]-4-hydroxy-5-oxo-2H-furan-3-olate Other names Calcium diascorbate; Calcium L-ascorbate; Hemicalcium ascorbate; Calci-C; E 302 Identifiers CAS Number 5743-27-1 Y 3D model (JSmol) Interactive image ChemSpider 4445637 Y ECHA InfoCard 100.126.521 E number E302 (antioxidants, ...) PubChem CID 21967 UNII J96U0ZD4Y6 Y CompTox Dashboard (EPA) DTXSID3047687 InChI InChI=1S/2C6H8O6.Ca.2H2O/c2*7-1-2(8)5-3(9)4(...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

German badminton player (born 1984) Badminton playerJohannes SchöttlerPersonal informationCountryGermanyBorn (1984-08-27) 27 August 1984 (age 39)Hamburg, West GermanyHeight1.92 m (6 ft 4 in)Weight84 kg (185 lb)HandednessRightMen's & mixed doublesHighest ranking11 (MD 28 April 2011)24 (XD 21 January 2010) Medal record Men's badminton Representing Germany European Mixed Team Championships 2013 Moscow Mixed team 2011 Amsterdam Mixed team 2015 Leuven Mixed...

48°49′43″N 2°13′21″E / 48.82861°N 2.22250°E / 48.82861; 2.22250 French porcelainClodion vase. Hard-paste porcelain and gilt bronze, 1817. Manufacture nationale de Sèvres Rouen (1673–96) Saint-Cloud (1693–1766) Chantilly (1730–1800) Vincennes (1740–56) Mennecy (1745–65) Sèvres (1756–present) Etiolles (1766–?) Revol (1768–present) Limoges (1771–present) Clignancourt (1775–1790) Dihl and Guérhard (1781–1828) Nast (1783–1835) Franço...

UN Secretariat department that promotes human rights under international law For similarly named entities, see United Nations human rights organization (disambiguation).Office of the United Nations High Commissioner for Human RightsAbbreviationOHCHRHCDHFormation20 December 1993[1]TypeAgencyLegal statusActiveHeadquartersGeneva, SwitzerlandNew York City, United StatesHeadVolker Türk(High Commissioner for Human Rights)[2]Websiteohchr.org The Office of the United Nations High Com...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2021) المستشار أحمد العجيل رئيس المجلس الأعلى للقضاء الكويتي في المنصب20 أكتوبر 2020 – حتى الآن رئيس محكمة التمييز الكويتية في المنصب20 أكتوبر 2020 – حتى الآن معلومات...

Skyscraper in Sydney, Australia Quay Quarter TowerQuay Quarter Tower, March 2023General informationStatusCompletedTypeCommercialLocation50 Bridge Street, Sydney, AustraliaCoordinates33°51′47″S 151°12′41″E / 33.86306°S 151.21146°E / -33.86306; 151.21146Opening1976Renovated2018–2021OwnerMirvac Wholesale Office FundDexus Wholesale Property FundRest SuperHeight188 m (617 ft) (1976–2018)216 m (709 ft) (2022–present)Technical detailsFloo...

العلاقات المالديفية النيجرية جزر المالديف النيجر المالديف النيجر تعديل مصدري - تعديل العلاقات المالديفية النيجرية هي العلاقات الثنائية التي تجمع بين المالديف والنيجر.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وج...

William Peter BlattyBlatty pada 2009Lahir(1928-01-07)7 Januari 1928New York City, Amerika SerikatMeninggal12 Januari 2017(2017-01-12) (umur 89)Bethesda, Maryland, Amerika SerikatPekerjaan Novelis penulis naskah sutradara AlmamaterUniversitas GeorgetownUniversitas George WashingtonGenreHoror, drama, komediPasanganMary Margaret Rigard (m. 1950; bercerai 1963) Elizabeth Gilman (m. 1965; bercerai 197...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2023) جزء من من سلسلة مقالات حولالديانات الإفريقيّة التقليديّة العقائد الكهانة نومو [الإنجليزية] فهرس الأساطير الإفريقية الفلسفة ديانة سيريرية الآلهة فهرس الآل...

Сатым Улуг-Зодатадж. Сотим Улуғзода Дата рождения 11 сентября 1911(1911-09-11) Место рождения кишлак Варзык, Наманганский уезд, Ферганская область, Российская империя Дата смерти 25 июня 1997(1997-06-25) (85 лет) Место смерти Душанбе, Таджикистан Гражданство Российская империя СССР&...

Cet article est une ébauche concernant une compétition de football et la Birmanie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Myanmar National League Généralités Sport Football Création 1996 Catégorie Division 1 Lieu(x) Birmanie Participants 10 Statut des participants Professionnels depuis 2009 Palmarès Tenant du titre Shan United FC (2023) Plus titré(s) Finance and Revenue FC (10) Pour la dernièr...

American singer and songwriter Peter YarrowYarrow in 2008Background informationBorn (1938-05-31) May 31, 1938 (age 86)New York City, USGenresFolkOccupationsSinger-songwriterguitaristrecord producerInstruments Vocals guitar Years active1950s-presentMember of Peter and Noel Paul (2009–present) Formerly of Peter, Paul and Mary (1961–1970; 1978–2008) Musical artist Peter Yarrow (born May 31, 1938) is an American singer and songwriter who found fame as a member of the 1960s folk trio Pe...

Concept in which the future affects the past Retrocausality, or backwards causation, is a concept of cause and effect in which an effect precedes its cause in time and so a later event affects an earlier one.[1][2] In quantum physics, the distinction between cause and effect is not made at the most fundamental level and so time-symmetric systems can be viewed as causal or retrocausal.[3][page needed] Philosophical considerations of time travel often addres...

Lega Nazionale B 1966-1967Lega Nazionale B Competizione Lega Nazionale B Sport Calcio Edizione 69ª Organizzatore ASF-SFV Luogo Svizzera Partecipanti 14 Formula Girone all'italiana Risultati Vincitore Lucerna(4º titolo) Promozioni Lucerna Bellinzona Retrocessioni Le Locle-Sports Blue Stars Zurigo Cronologia della competizione 1965-1966 1967-1968 Manuale La Lega Nazionale B 1966-1967, campionato svizzero di seconda serie, si concluse con la vittoria del FC Lucerna...

Species of Old World monkey Barbary macaqueTemporal range: Early Pliocene–Recent PreꞒ Ꞓ O S D C P T J K Pg N Young Barbary macaque with its mother Conservation status Endangered (IUCN 3.1)[2] CITES Appendix I (CITES)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Cercopithecidae Genus: Macaca Species: M. sylvanus[1] Binomial name...

Robecchetto con Indunocomune Robecchetto con Induno – Veduta LocalizzazioneStato Italia Regione Lombardia Città metropolitana Milano AmministrazioneSindacoSabrina Pane (commissario prefettizio) dal 03-04-2024 TerritorioCoordinate45°32′N 8°46′E45°32′N, 8°46′E (Robecchetto con Induno) Altitudine172 m s.l.m. Superficie13,93 km² Abitanti4 794[1] (30-6-2023) Densità344,15 ab./km² FrazioniMalvaglio, Induno Comuni confinantiCastano...