Read other articles:

Apristurus ampliceps Apristurus ampliceps Status konservasiRisiko rendahIUCN42701 TaksonomiKerajaanAnimaliaFilumChordataKelasChondrichthyesOrdoCarcharhiniformesFamiliScyliorhinidaeGenusApristurusSpesiesApristurus ampliceps lbs Apristurus ampliceps adalah sebuah spesies hiu kucing dalam keluarga Scyliorhinidae yang ditemukan di dekat Australia dan Selandia Baru.[2][3] Habitat alaminya adalah laut terbuka.[2] Spesies tersebut pertama kali dideskripsikan pada tahun 2008 o...

PanggabeanAksara Batakᯇᯰᯎᯅᯩᯀᯉ᯲ (Surat Batak Toba)Nama margaPanggabeanSilsilahJarakgenerasi denganSiraja Batak1Si Raja Batak2Raja Isumbaon3Tuan Sorimangaraja4Tuan Sorbadibanua (Raja Nai Suanon)5Si Raja Sobu6Raja Hasibuan7Guru Mangaloksa Hasibuan8PanggabeanNama lengkaptokohSi Raja PanggabeanNama istriboru PasaribuNama anak1. Lumban Ratus2. Simorangkir3. Lumban SiagianKekerabatanInduk margaGuru Mangaloksa HasibuanPersatuanmargaSi Opat PusoranKerabatmargaHutabaratHutagalungHutator...

Wali Kota PadangPetahanaHendri Septasejak 7 April 2021KediamanRumah Dinas Wali Kota PadangMasa jabatan5 tahun, sesudahnya dapat dipilih kembali sekaliDibentuk1945 (di bawah pemerintahan Indonesia)Pejabat pertamaAbdoel HakimSitus webwww.padang.go.id Wali Kota Padang adalah politisi yang dipilih untuk bertanggung jawab dalam mengatur dan mengelola pemerintahan Kota Padang, sebagai bagian dari sistem penyelenggaraan pemerintahan daerah di Indonesia. Abubakar Jaar adalah wali kota pertama se...

Russian politician In this name that follows Eastern Slavic naming customs, the patronymic is Vladimirovich and the family name is Plyakin. Vladimir PlyakinMPВладимир Плякинofficial portrait, circa 2021Member of the State Duma (Party List Seat)IncumbentAssumed office 12 October 2021 Personal detailsBorn (1981-09-19) 19 September 1981 (age 42)Kuybyshev, RSFSR, USSRPolitical partyNew PeopleEducationSamara Academy of State and Municipal ManagementMoscow City Pedagogica...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Branch of the National Institutes of Health in the United States For other uses, see NIDA (disambiguation). National Institute on Drug AbuseAgency overviewHeadquarters6001 Executive Blvd, N. Bethesda, Maryland 20852Annual budget$1.05 billion[1]Agency executiveNora D. Volkow, M.D., DirectorParent departmentU.S. Department of Health and Human ServicesParent agencyNational Institutes of HealthWebsitenida.nih.gov The National Institute on Drug Abuse (NIDA) is a United States federal gove...

2022 election in Delaware 2022 Delaware Attorney General election ← 2018 November 8, 2022 2026 →   Nominee Kathy Jennings Julianne Murray Party Democratic Republican Popular vote 171,837 147,369 Percentage 53.8% 46.2% County results Precinct resultsJennings:      50–60%      60–70%      70–80%      80–90%      >90%Murray:  ...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Not to be confused with Southern Beltway or Southern Boulevard Parkway. Limited-access highway in Long Island, NY Southern State ParkwaySouthern State Parkway highlighted in redRoute informationMaintained by NYSDOTLength25.53 mi[1] (41.09 km)Existed1927[2]–presentRestrictionsNo commercial vehiclesMajor junctionsWest end Belt Parkway / Cross Island Parkway in Valley StreamMajor intersections Meadowbrook State Parkway in North Merrick Wantagh State Par...

German footballer Johannes Rahn Personal informationFull name Johannes RahnDate of birth (1986-01-16) 16 January 1986 (age 38)Place of birth Hachenburg, West GermanyHeight 1.90 m (6 ft 3 in)Position(s) ForwardTeam informationCurrent team Eintracht WindhagenNumber 13Youth career0000–2002 JSG Alpenrod/Nistertal2002–2003 VfL Hamm/Sieg2003–2004 TuS KoblenzSenior career*Years Team Apps (Gls)2004–2007 TuS Koblenz 56 (3)2007–2009 VfB Stuttgart II 59 (11)2009–2011 TuS ...

Tuhan Memberkati oleh artis Inggris Edmund Leighton, 1900: memperlihatkan ksatria berlapis baja meninggalkan istri/kasih sayang dia untuk perang. Bagian dari seri tentangCintaRed-outline heart icon Jenis-jenis cinta Afeksi Ikatan Patah hati Cinta yang penuh kasih Cinta konjugal Cinta bahaduri Pacaran Troubadour Jatuh cinta Persahabatan cross-sex romantis Zona pertemanan Keramahan Hubungan antar pribadi Intimasi Limerence Kecanduan cinta Cinta pada pandangan pertama Cinta segitiga Penyakit cin...

1832 treaty between the United States and Seminole The Treaty of Payne's Landing (Treaty with the Seminole, 1832) was an agreement signed on 9 May 1832 between the government of the United States and several chiefs of the Seminole Indians in the Territory of Florida, before it acquired statehood. Background A contemporary map of the reservation assigned to the Seminole Indians in the Treaty of Moultrie Creek By the Treaty of Moultrie Creek in 1823, the Seminoles had relinquished all claims to...

American bull rider Tuff HedemanHedeman at Las Vegas Motor Speedway in 2024BornRichard Neale Hedeman (1963-03-02) March 2, 1963 (age 61)[1]El Paso, Texas, U.S.Alma materSul Ross State UniversityOccupationsBull riding event producerRancher and team roperRetired rodeo contestantYears active1980-1993; 1995-1998 (as a professional bull rider)Spouse(s)Tracy Stepp (married 1986-2015)Liz Rippetoe (married 2021-present)Children4 Richard Neale Tuff Hedeman (born March 2, 1963) i...

                                            الثقافة الأعلام والتراجم الجغرافيا التاريخ الرياضيات العلوم المجتمع التقانات الفلسفة الأديان فهرس البوابات عدل   بوابة تعمية علم التعمية أو علم التشفير أو الكريبتولوجيا (باللاتيني...

Bilateral relationsPakistan-Malta relations Pakistan Malta Malta–Pakistan relations are the bilateral relations between Malta and Pakistan. Neither country has a resident ambassador. Pakistan is concurrently accredited to Malta through its embassy in Tunis with an Honorary Consulate in Attard (Malta) since September 2015.[1] Both countries are full members of the Commonwealth of Nations. High level interaction Bilateral meetings have always emphasized the need for increasing commerc...

Football clubEpitsentr Kamianets-PodilskyiFull nameFC Epitsentr Kamianets-PodilskyiFounded1960GroundTonkocheyev StadiumKolos StadiumCapacity2,587[1][2]2,500ChairmanIvan ChernonohManagerSerhiy NahornyakLeagueUkrainian First League2022–23Ukrainian First League, 6th of 16WebsiteClub website Home colours Away colours Third colours Former logo INAPiK 2007–2013 Logo in 2019–2022 FC Epitsentr Kamianets-Podilskyi (Ukrainian: Футбольний клуб «Епіцентр» К�...

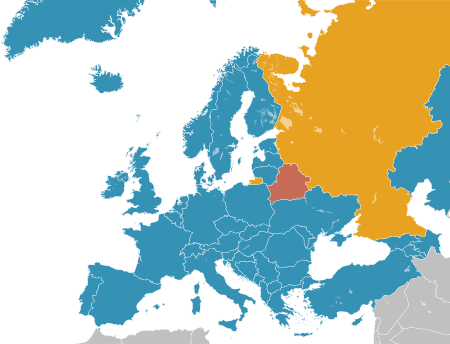
Europe holds the greatest concentration of abolitionist states (blue). Map current as of 2022   Abolished for all offences   Abolished in practice   Retains capital punishment Norwegian executioner's axe from 1742Norwegian National Museum of Justice Capital punishment in Norway (Norwegian: dødsstraff) has been constitutionally prohibited since 2014. Before that, it had been fully abolished in 1979, and earlier, from 1905, the penal code had abolished capital pu...

جزء من سلسلة مقالات سياسة إيطالياإيطاليا الدستور الدستور حقوق الإنسان السلطة التنفيذية الرئيس مجلس الوزراء السلطة التشريعية البرلمان السلطة القضائية القضاء الانتخابات الانتخابات الأحزاب السياسية السياسة الخارجية العلاقات الخارجية إيطاليا السياسةعنت الجمهورية الإيط�...

この項目には、JIS X 0213:2004 で規定されている文字（ハートマーク）が含まれています（詳細）。 『リルぷりっ』は、セガと小学館が共同開発したトレーディングカードゲーム方式の女児向けアーケードゲーム『リルぷりっ ゆびぷるひめチェン!』、およびそれに関連した日本の漫画、テレビアニメ作品『ひめチェン!おとぎちっくアイドル リルぷりっ』。当該作品に登�...

Grafico della funzione degli errori La funzione degli errori (chiamata anche funzione degli errori di Gauss), in matematica, è una funzione speciale che si incontra in probabilità, in statistica e nelle equazioni differenziali alle derivate parziali. Si definisce come: erf ⁡ ( x ) := 2 π ∫ 0 x e − t 2 d t , {\displaystyle \operatorname {erf} (x):={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t,} valida per ogni numero reale x ; {\displaystyle x;} ...