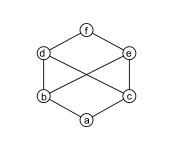
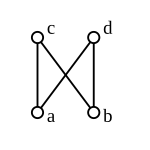
Kekisi (tatanan)
|
Read other articles:

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Halaman ini berisi artikel tentang kota di Toscana, Italia. Untuk karakter dalam seri novel Harry Potter, lihat Firenze (Harry Potter). FirenzeKom...

Cekakak sungai Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Coraciiformes Famili: Alcedinidae Genus: Todirhamphus Spesies: T. chloris Nama binomial Todiramphus chloris(Boddaert, 1783) Sinonim Halcyon chloris Todirhamphus chloris Cekakak sungai (bahasa Latin = Todirhamphus chloris) adalah spesies burung dari keluarga Alcedinidae, dari genus Todirhamphus. Burung ini merupakan jenis burung pemakan kadal, ...

Agence de gestion et de recouvrement des avoirs saisis et confisquésHistoireFondation 9 juillet 2010CadreSigle AGRASCType Établissement public administratifForme juridique Établissement public national à caractère administratifDomaines d'activité Confiscation, administration publique généraleSiège 2e arrondissement de Paris (98-102, rue de Richelieu)Pays FranceOrganisationAffiliation Ministère de la Justice, ministère de l'Action et des Comptes publicsSite web www.justice.gou...

Toshiyuki NishidaNishida pada tahun 2018Nama asal西田 敏行Lahir04 November 1947 (umur 76)Fukushima, JepangKebangsaanJepangPekerjaanPemeran, EksekutifTahun aktif1967–sekarang Toshiyuki Nishida (西田 敏行code: ja is deprecated , Nishida Toshiyuki, lahir 4 November 1947) adalah pemeran Jepang. Ia memenangkan dua Japanese Academy Awards untuk pemeran pria terbaik, untuk The Silk Road (1988) dan Tsuribaka Nisshi 6 (1993). Ia juga memenangkan Blue Ribbon Award untuk pemera...

PausViktor IIIAwal masa kepausan24 Mei 1086Akhir masa kepausan16 September 1087PendahuluGregorius VIIPenerusUrbanus IIInformasi pribadiNama lahirDauferiusLahir±1026Benevento, ItaliaWafat16 September 1087Monte Cassino, ItaliaPaus lainnya yang bernama Viktor Viktor III, nama lahir Dauferius (Benevento, Italia, ±1026 – Monte Cassino, Italia, 16 September 1087), adalah Paus Gereja Katolik Roma sejak 24 Mei 1086 sampai 16 September 1087. lbs Paus Gereja Katolik Daftar paus grafik masa jabatan ...

Chemical compound LasofoxifeneClinical dataTrade namesFablynRoutes ofadministrationBy mouthDrug classSelective estrogen receptor modulatorATC codeG03XC03 (WHO) Identifiers IUPAC name (5R,6S)-6-phenyl-5-[4-(2-pyrrolidin-1-ylethoxy)phenyl]-5,6,7,8-tetrahydronaphthalen-2-ol CAS Number180916-16-9 NPubChem CID216416IUPHAR/BPS7542ChemSpider187585 YUNII337G83N988ChEBICHEBI:135938ChEMBLChEMBL328190 YCompTox Dashboard (EPA)DTXSID50171037 Chemical and physical dataFormulaC28H31...

Local government building in the United States Hamilton County CourthouseWestern front of the courthouseLocation within OhioGeneral informationLocation1000 Main Street,Cincinnati, Ohio 45202Coordinates39°6′25.67″N 84°30′37.09″W / 39.1071306°N 84.5103028°W / 39.1071306; -84.5103028Completed1915 The Hamilton County Courthouse is located in downtown Cincinnati, Ohio and contains the Hamilton County Common Pleas Court, the Municipal Court, Small Claims Court, a...

U.S. House district for Virginia Virginia's 3rd congressional districtInteractive map of district boundaries since 2023Representative Bobby ScottD–Newport NewsDistribution95.01% urban[1]4.99% ruralPopulation (2022)781,088[2]Median householdincome$63,075[3]Ethnicity43.2% Black39.0% White8.4% Hispanic5.4% Two or more races3.0% Asian1.1% otherCook PVID+17[4] Virginia's 3rd congressional district from January 3, 2023 Virginia's third congressional district ...

Assyabaab BangilNama lengkapAssyabaab BangilBerdiri1920StadionStadion R. SoedarsonoBangil, Pasuruan(Kapasitas: 10.000)PemilikPSSI Kabupaten PasuruanKetuaMohammad BahalwanLigaLiga 32017Posisi ke-5 Grup zona Jawa TimurSitus webSitus web resmi klub Kostum kandang Kostum tandang Assyabaab Bangil adalah klub sepak bola amatir yang bermarkas di Stadion R. Soedarsono, Pogar, Bangil, Kabupaten Pasuruan. Assyabaab Bangil saat ini berkompetisi di Liga 3 Zona Jawa Timur.[1] Referensi ^ 41 K...

Quartiere ValsesiaLocalizzazioneStato Italia RegioneLombardia LocalitàMilano Coordinate45°27′14.4″N 9°05′53.05″E / 45.454°N 9.09807°E45.454; 9.09807Coordinate: 45°27′14.4″N 9°05′53.05″E / 45.454°N 9.09807°E45.454; 9.09807 Informazioni generaliCondizioniIn uso CostruzioneAnni '70 UsoResidenziale RealizzazioneCommittenteACLI Modifica dati su Wikidata · Manuale Quartiere Valsesia è un complesso di edilizia residenziale di Milan...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

American baseball player, manager, and executive Baseball player Paul RichardsCatcher / ManagerBorn: (1908-11-21)November 21, 1908Waxahachie, Texas, U.S.Died: May 4, 1986(1986-05-04) (aged 77)Waxahachie, Texas, U.S.Batted: RightThrew: RightMLB debutApril 17, 1932, for the Brooklyn DodgersLast MLB appearanceSeptember 22, 1946, for the Detroit TigersMLB statisticsBatting average.227Home runs15Runs batted in155Managerial record923–901Winning %.506 TeamsA...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2020) (Learn how and when to remove this message) The Port Olímpic (English: Olympic Harbour) is a marina located in Barcelona, Catalonia. Located east of the Port of Barcelona, it hosted the sailing events for the 1992 Summer Olympics. It will be the main venue for ...

В Википедии есть статьи о других людях с такой фамилией, см. Носов; Носов, Сергей. Сергей Носов Дата рождения 19 февраля 1957(1957-02-19) (67 лет) Место рождения Ленинград Гражданство СССР Россия Образование Литературный институт имени А. М. ГорькогоСанкт-Петербургский госуд�...

У этого термина существуют и другие значения, см. Тала. Тала[a] самоан. Tālā англ. Tala[b] фр. Tala[b] 1 тала 1972 года1 тала 1976 года Коды и символы Коды ISO 4217 WST (882) Символы $ • WS$ Аббревиатуры SAT, ST, T Территория обращения Страна-эмитент Самоа Производные и параллел�...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (نوفمبر 2020) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة �...

High schoolLiceo Industrial de San FernandoLocationSan Fernando, ChileInformationTypeHigh school Liceo Industrial de San Fernando (English: San Fernando Industrial High School) is a Chilean high school located in San Fernando, Colchagua Province, Chile.[1] References ^ Tabla de Directorio Oficial de Establecimientos Año 2010 (in Spanish). Ministry of Education (Chile). December 2010. Archived from the original on 29 September 2017. Retrieved 5 July 2012. This Chilean school-related a...