1996 GQ
| |||||||||||||||||||||||||
Read other articles:
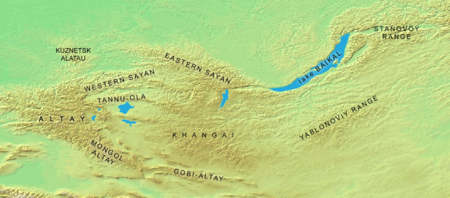
Geografi Mongolia BenuaAsiaKawasanAsia TimurKoordinat46°0′N 105°0′E / 46.000°N 105.000°E / 46.000; 105.000WilayahPeringkat 181.564.116 km² (603.908,6 mil²)99,3% daratan0,7% perairanPerbatasanRusia: 3.485 kilometer (2.165 mi) Tiongkok: 4.676 kilometer (2.906 mi)Titik tertinggiPuncak Khüiten 4.374 m (14.350 ft)Titik terendahHoh Nuur 560 m (1.840 ft)Sungai terpanjangSungai Orkhon1.124 kilometer (698 mi)Danau terbesa...

Jean-Marie Roland de la Platièrefrom Édouard Charton, Le Magasin Pittoresque, 1777 à 1786Lahir(1734-02-18)18 Februari 1734Thizy, PrancisMeninggal15 November 1793(1793-11-15) (umur 59)Bourg-Beaudouin, PrancisSebab meninggalbunuh diriTempat tinggalThizy, Kyons, Languedoc, Picardy, ParisKebangsaanPrancisPekerjaanekonomTempat kerjaRaja Louis XVIDikenal ataspemimpin faksi GirondisKota asalLyon, PrancisGelarMenteri Dalam Negeri, Menteri KeadilanPartai politikGirondeLawan politikR...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Kerajinan – berita · surat kabar · buku · cendekiawan · JSTOR Perajin wayang kulit di Yogyakarta. Kerajinan adalah hobi atau pekerjaan yang membutuhkan kemampuan dan pengetahuan tertentu untuk menciptaka...

2017 single by DJ Khaled featuring Justin Bieber, Quavo, Chance the Rapper, and Lil Wayne Not to be confused with I'm on One. I'm the OneSingle by DJ Khaled featuring Justin Bieber, Quavo, Chance the Rapper, and Lil Waynefrom the album Grateful ReleasedApril 28, 2017 (2017-04-28)Recorded2016–2017GenreHip hop[1]pop-rap[2]Length4:49LabelWe the BestEpicSongwriter(s)Khaled KhaledJustin BieberQuavious MarshallChancelor BennettDwayne Carter Jr.Nicholas BaldingJason ...

Semi-permanent joint between two ropes This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rope splicing – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Stages in splicing the end of a rope, from Scientific American, 1871 Rope splicing in ropewor...

Cet article est une ébauche concernant la protection des cultures. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Les maladies de la patate douce (Ipomoea batatas (L.) Lam.) sont nombreuses et peuvent affecter les plants en phase de culture, mais aussi les tubercules stockés. Elles sont causées par des agents pathogènes très divers : bactéries, champignons, protistes, virus, phytoplasmes, etc., par d...

Probability density of electrons being somewhere This article is about the quantum mechanical probability density of an electron. For the number density of electrons in a plasma, also called electron density, see Plasma (physics). Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either ...

1938 EuropeanAthletics ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmen800 mmen1500 mmen5000 mmen10,000 mmen80 m hurdleswomen110 m hurdlesmen400 m hurdlesmen3000 msteeplechasemen4×100 m relaymenwomen4×400 m relaymenRoad eventsMarathonmen50 km walkmenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin throwmenwomenCombined eventsDecathlonmenvte The men's 200 metres at the 1938 European Athletics Champ...

لمعانٍ أخرى، طالع ثقة (توضيح). ثقةمعلومات عامةصنف فرعي من عقيدة جزء من مصطلحات علم النفس يدرسه نظرية العاطفة يستخدمه حيلة الائتمان النقيض الارتياب تعديل - تعديل مصدري - تعديل ويكي بيانات كلمة ثقة مكتوبة بالعربية والإنجليزية على حائط في بغداد. الثقة هي علاقة اعتماد بي�...

Museo Marítimo Nacional National Maritime Museum Patrimonio de la Humanidad (parte de «Greenwich marítimo») (1997) Vista exterior del museoUbicaciónPaís Reino Unido Reino UnidoDivisión Inglaterra InglaterraSubdivisión Gran LondresMunicipio Municipio de GreenwichLocalidad GreenwichCoordenadas 51°28′52″N 0°00′20″O / 51.4811, -0.005556Tipo y coleccionesSuperficie 200 acres (0,81 km²)Historia y gestiónCreación 1937Inauguración 1937Director Kev...

Sarah Al AmiriSarah Al Amiri pada 2019 Menteri Negara Ilmu Pengetahuan Tingkat LanjutPetahanaMulai menjabat 1 Oktober 2017Perdana MenteriMohammed bin RashidPendahuluPosisi baruPenggantiPetahana Informasi pribadiLahir1987 (umur 36–37)Alma materAmerican University of SharjahSunting kotak info • L • B Sarah bint Yousif Al Amiri (lahir 1987) adalah ilmuwan dan ketua Dewan Ilmuwan Uni Emirat Arab (UEA). Ia menjabat sebagai manajer dan insinyur untuk proyek Emirates Mar...

2004 American comedy-drama film by Alexander Payne This article is about the film. For other uses, see Sideways (disambiguation). SidewaysTheatrical release posterDirected byAlexander PayneScreenplay by Alexander Payne Jim Taylor Based onSidewaysby Rex PickettProduced byMichael LondonStarring Paul Giamatti Thomas Haden Church Virginia Madsen Sandra Oh CinematographyPhedon PapamichaelEdited byKevin TentMusic byRolfe KentProductioncompanyMichael London ProductionsDistributed byFox Searchlight P...

العلاقات السلوفينية اللاوسية سلوفينيا لاوس سلوفينيا لاوس تعديل مصدري - تعديل العلاقات السلوفينية اللاوسية هي العلاقات الثنائية التي تجمع بين سلوفينيا ولاوس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة...

Railway station in Suzhou, Anhui, China Dangshannan砀山南General informationOther namesDangshan SouthLocationDangshan County, Suzhou, AnhuiChinaCoordinates34°23′16″N 116°17′54″E / 34.3879°N 116.2983°E / 34.3879; 116.2983Operated by CR ShanghaiLine(s) Xuzhou–Lanzhou High-Speed RailwayPlatforms2Tracks4HistoryOpened10 September 2016 [1]Services Preceding station China Railway High-speed Following station Yongcheng Northtowards Xuzhou East Xuzhou�...

Fictional DC comics character, created 1985 Comics character Superboy-PrimeSuperboy-Prime in his Anti-Monitor inspired armor. Cover to Infinite Crisis #6 (2006).Publication informationPublisherDC ComicsFirst appearanceDC Comics Presents #87 (November 1985)Created byElliot S. Maggin Curt SwanIn-story informationAlter egoKal-ElClark KentSpeciesKryptonianPlace of originEarth Prime, born on Krypton of same universeTeam affiliationsSinestro CorpsLegion of Super-VillainsLegion of DoomRed Lantern Co...

German armored division 4th SS Polizei Panzergrenadier DivisionDivisional insigniaActive1939–45Country Nazi GermanyBranch Waffen-SSTypeInfantryPanzergrenadierSizeDivisionCommandersNotablecommandersKarl Pfeffer-WildenbruchAlfred Wünnenberg Karl SchümersMilitary unit The 4th SS Polizei Panzergrenadier Division (4. SS-Polizei-Panzergrenadier-Division) or SS Division Polizei was one of the thirty-eight divisions fielded as part of the Waffen-SS during World War II. Formation The division...

Protection of wilderness areas in the U.S. The Wilderness Act protects exceptionally undisturbed natural areas and scenery, such as in the Ansel Adams Wilderness. The National Wilderness Preservation System (NWPS) of the United States protects federally managed wilderness areas designated for preservation in their natural condition. Activity on formally designated wilderness areas is coordinated by the National Wilderness Preservation System. Wilderness areas are managed by four federal land ...

СтанцияКиров-КотласскийКиров — КотласГорьковская железная дорога 58°36′21″ с. ш. 49°38′38″ в. д.HGЯO Регион ж. д. Кировский регион Дата открытия 1899 год[1] Прежние названия Вятка, Вятка-II (до 1934)[2], Вятка-Пермская, Вятка-Котласская Количество платформ 1 Количест...

シーフシュピーグラー式望遠鏡 シーフシュピーグラー式望遠鏡(Schiefspiegler telescope )は反射望遠鏡の一形式である。 主鏡は凹面[1]、副鏡は凸面[1]である。焦点までの間にもう1枚弱い凹面鏡を入れる場合もある[1]が、F15くらいの長焦点であれば主鏡副鏡は同一曲面で3枚目の鏡を省略できる[1]。 光軸を外しているためコマ収差が起こりやすくF10以...

146 магнитных шариков, образующие октаэдр Октаэдральное число — разновидность многогранных фигурных чисел. Поскольку октаэдр можно рассматривать как две квадратные пирамиды, склеенные своими основаниями (см. рисунок), октаэдральное число определяется как сумма двух по�...