Thalész-tétel
|
Read other articles:
Karate padaPekan Olahraga Nasional XIX Kata Putra Putri Perorangan Perorangan Beregu Beregu Kumite Putra Putri Beregu Beregu 55 kg 50 kg 60 kg 55 kg 67 kg 61 kg 75 kg 68 kg 84 kg +68 kg +84 kg Karate nomor Kumite 84 kg putra pada Pekan Olahraga Nasional XIX dipertandingkan pada 18 September 2016[1] di Sasana Budaya Ganesha, Institut Teknologi Bandung, Kota Bandung, Jawa Barat. Pertandingan karate menggunakan s...

Huta GodangDesaKantor Kepala Desa Huta GodangNegara IndonesiaProvinsiSumatera UtaraKabupatenTapanuli SelatanKecamatanBatang ToruKode pos22738Kode Kemendagri12.03.02.2004 Luas8 km²Jumlah penduduk272 jiwa Huta Godang merupakan salah satu desa yang ada di kecamatan Batang Toru, Tapanuli Selatan, Sumatera Utara, Indonesia. Desa ini terletak di sebelah barat Kabupaten Tapanuli Selatan yang berbatasan langsung dengan wilayah Kecamatan Sibabangun, Kabupaten Tapanuli Tengah. Desa ini juga memil...

Peta Wilayah Desa Wonosido WonosidoDesaNegara IndonesiaProvinsiJawa TengahKabupatenPurworejoKecamatanPituruhKode pos54263Kode Kemendagri33.06.11.2048 Luas5 km²Jumlah penduduk1200 jiwaKepadatan240 jiwa/km² Untuk kegunaan lain, lihat Wonosido (disambiguasi). Wonosido merupakan salah satu desa di kecamatan Pituruh, Purworejo, Jawa Tengah, Indonesia. Desa Wonosido terletak sekitar ±12 km dari pusat kecamatan Pituruh serta 32 km dari pusat Kabupaten Purworejo melalui Pituruh atau...

Tamás Kádár Informasi pribadiNama lengkap Tamás KádárTanggal lahir 14 Maret 1990 (umur 34)Tempat lahir Veszprém, HungariaTinggi 1,88 m (6 ft 2 in)Posisi bermain BekInformasi klubKlub saat ini Roda JCNomor 23Karier junior2004–2006 Zalaegerszegi TEKarier senior*Tahun Tim Tampil (Gol)2006–2008 Zalaegerszegi TE 14 (1)2008– Newcastle United 13 (0)2011 → Huddersfield Town (pinjaman) 2 (0)2012– Roda JC 4 (0)Tim nasional‡2006 Hungaria U-17 6 (0)2007 Hungaria U-...

УсадьбаБольшие Горки 55°30′17″ с. ш. 37°45′52″ в. д.HGЯO Страна Россия Местоположение Горки Ленинские Статус Объект культурного наследия народов РФ федерального значения. Рег. № 501420777940006 (ЕГРОКН). Объект № 5010232000 (БД Викигида) Медиафайлы на Викискладе Об �...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Hotel in Portland, Oregon, U.S. Hotel EastlundFrom the southwest in 2015, when only recently renamedFormer namesCosmopolitan Motor Hotel (1962–1989)[1]ExeculodgeHoliday Inn DowntownRed Lion Hotel Portland – Convention Center (2003–2014)General informationTown or cityPortland, OregonCountryUnited StatesCoordinates45°31′50″N 122°39′39″W / 45.53056°N 122.66083°W / 45.53056; -122.66083Opened1962Other informationPublic transit accessTriMet MAX Ligh...

Variation of gridiron football played at ice hockey-sized indoor arenas Arena footballSan Jose SaberCats and Columbus Destroyers in ArenaBowl XXI, the 2007 championship game of the AFLNicknamesArena football, indoor football, football, gridiron footballFirst played1980'sCharacteristicsContactFullTeam members8 at a timeTypeIndoor pro football Arena football is a variety of eight-man indoor gridiron football. The game is played indoors on a smaller field than American or Canadian football, desi...

Diode that allows current to flow in the reverse direction at a specific voltage Zener diodeZener diodeTypePassiveWorking principleZener effectInventedClarence Melvin ZenerPin configuration Anode and cathodeElectronic symbol A Zener diode is a special type of diode designed to reliably allow current to flow backwards (inverted polarity) when a certain set reverse voltage, known as the Zener voltage, is reached. Zener diodes are manufactured with a great variety of Zener voltages a...

Jewish religious male circumcision ceremony Part of a series onJudaism Movements Orthodox Haredi Hasidic Modern Conservative Conservadox Reform Karaite Reconstructionist Renewal Humanistic Haymanot Philosophy Principles of faith Kabbalah Messiah Ethics Chosenness God Names Musar movement Texts Tanakh Torah Nevi'im Ketuvim Ḥumash Siddur Piyutim Zohar Rabbinic Mishnah Talmud Midrash Tosefta Law Mishneh Torah Tur Shulchan Aruch Mishnah Berurah Aruch HaShulchan Kashrut T...

HectometreThe Great Pyramid of Giza is 137.7 metres high, which is 1.377 hectometres.General informationUnit systemSIUnit oflengthSymbolhmConversions 1 hm in ...... is equal to ... SI base units 100 m imperial/US units 109.36 yd 3937.0 in SI unit of length The hectometre (International spelling as used by the International Bureau of Weights and Measures; SI symbol: hm[1]) or hectom...

2024 mixed martial event in Nevada, US UFC on ABC: Whittaker vs. AliskerovThe poster for UFC on ABC: Whittaker vs. AliskerovInformationPromotionUltimate Fighting ChampionshipDateJune 22, 2024 (2024-06-22)VenueKingdom ArenaCityRiyadh, Saudi ArabiaEvent chronology UFC on ESPN: Perez vs. Taira UFC on ABC: Whittaker vs. Aliskerov UFC 303: Pereira vs. Procházka 2 UFC on ABC: Whittaker vs. Aliskerov (also known as UFC on ABC 6) is an upcoming mixed martial arts event produced by the...

German free climber This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2020) (Learn how and when to remove this message) Fritz WiessnerWiessner, age 86, on the Rupley Towers, Mount Lemmon, ArizonaBorn(1900-02-26)February 26, 1900Dresden, GermanyDiedJuly 3, 1988(1988-07-03) (aged 88)CitizenshipU.S. (after 1935)Known forPioneer of free climbingS...

Business process outsourcing and professional services company For the Latin phrase, see Per capita. For the Angolan footballer, see Capita (footballer). Capita plcFormerlyKnown Limit Limited (1986–1987)Capita Limited (March–April 1987)Capita Holdings Limited (1987–1988)The Capita Group PLC (1988–2012)[1]Company typePublic limited companyTraded asLSE: CPIIndustryBusiness process outsourcingProfessional servicesFounded1984HeadquartersLondon, EnglandKey peopleDavid Lowden (...

Coat of arms of the Royal Bavarian State Railways Owner's inscription on a goods wagon The Royal Bavarian State Railways (Königliche Bayerische Staats-Eisenbahnen or K.Bay.Sts.B.) was the state railway company for the Kingdom of Bavaria. It was founded in 1844. The organisation grew into the second largest of the German state railways (after that of the Prussian state railways) with a railway network of 8,526 kilometres (including the Palatinate Railway or Pfalzbahn) by the end of the First...

Pour les articles homonymes, voir Burnaby (homonymie). Davy BurnabyBiographieNaissance 7 avril 1881BucklandDécès 18 avril 1949 (à 68 ans)Nationalité britanniqueFormation Haileybury and Imperial Service College (en)Activité ActeurPère Henry Fowke Burnaby (d)Conjoint Maude Lambert (d)modifier - modifier le code - modifier Wikidata Davy Burnaby ou George Davy-Burnaby (né le 7 avril 1881 à Buckland, Hertfordshire, en Angleterre - mort le 18 avril 1949 à Angmering, Sussex en Anglete...
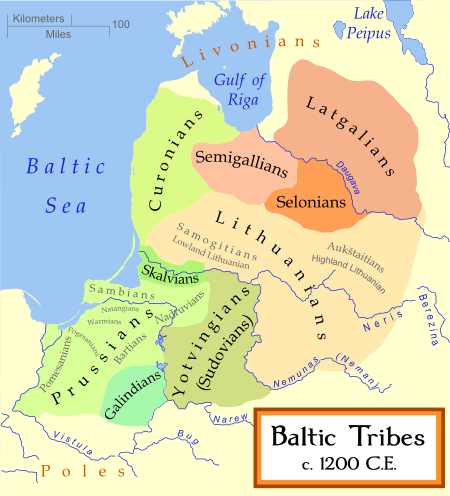
Den här artikeln behöver källhänvisningar för att kunna verifieras. (2015-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. Lettlands historia Denna artikel är en del av en serie Tidig historiaKundakulturen (ca 8000–5000 f.Kr.)Narvakulturen (ca 5300–1750 f.Kr.)Stridsyxekulturen (ca 2950-2300 f.Kr.)Liver och Balterkulturen (ca 2000 f.Kr.-...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: Huawei P20 lite – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2018年12月) HUAWEI P20 lite サクラピンク色の背面ブランド HUAW...




































































