A geometriában a Schläfli-szimbólum sokszögeket, poliédereket és magasabb dimenziós politópokat, parkettázásokat, térkitöltéseket ír le. A svájci Ludwig Schläfli után nevezték el.

Alakja ${\displaystyle \left\{p,q,r,\dots \right\}}$, ahol, ha ${\displaystyle {p}}$ egész, akkor egy megfelelő oldalszámú sokszöget jelöl. Ha tört, akkor egy csillagsokszöget jellemez, ahol a számláló a csúcsok számát, a nevező pedig azt adja meg, hogy körbemenve hányadik pontokat kell összekötni.

A Schläfli-szimbólumban szereplő számok sorrendjének megfordítása az eredetileg leírt objektum duálisát írja le.

A Schläfli-szimbólum egy rekurzív leírás, ami a ${\displaystyle \left\{p\right\}}$ sokszögből indul ki. A ${\displaystyle \left\{p,q\right\}}$ szimbólumban q azt adja meg, hogy a p sokszögből hány találkozik egy csúcsban. Ha egy négy dimenziós politópban minden él körül r ${\displaystyle \left\{p,q\right\}}$ szimbólumú poliéder találkozik, akkor Schläfli-szimbóluma ${\displaystyle \left\{p,q,r\right\}}$, és így tovább. A poliédereknek lehetnek csillagsokszög lapjaik is.

A ${\displaystyle \left\{p,q,r,...,y,z\right\}}$ szabályos politóp lapjának Schläfli-szimbóluma ${\displaystyle \left\{p,q,r,\dots ,y\right\}}$. Ugyanennek a poliédernek a csúcsalakzata ${\displaystyle \left\{q,r,\dots ,y,z\right\}}$.

A poliédereknek lehetnek csillagsokszög lapjaik is.

A szimbólum reprezentálhat véges sokszöget, poliédert, politópot, vagy euklideszi vagy hiperbolikus szabályos parkettát vagy térkitöltést a defektusától^{[* 1]} függően. Ha a defektus pozitív, akkor lapok felhajtogathatók az eggyel magasabb dimenziós térbe, így politópot alkothatnak. A nulla defektus azt jelzi, hogy az illeszkedő lapok kitöltik az adott dimenziójú euklideszi teret. A negatív defektus nem lehetséges az euklideszi térben, de a hiperbolikus térben már igen.

A csúcsalakzatot többnyire véges politópnak fogják fel, de néha érdemesebb parkettázásnak vagy térkitöltésnek tekinteni.

A szabályos politópok duálisainak Schläfli-szimbóluma megegyezik az eredeti Schläfli-szimbólum megfordításával. Az önduális politópok Schläfli-szimbóluma így szimmetrikus.

A Schläfli-szimbólum szorosan kapcsolódik az azonos indexű tükörszimmetrikus csoportokhoz, amelyeket Coxeter-csoportoknak is neveznek, és szögletes zárójelbe tesznek. Így a [3,3] Coxeter-csoport a tetraéder, a [3,4] az oktaéder, és [3,5] az ikozaéder tükörszimmetriái által generált csoport jele.

${\displaystyle \left\{n\right\}}$ egy ${\displaystyle n}$-szög.

${\displaystyle \left\{5/2\right\}}$ a pentagramma .

${\displaystyle \left\{7/2\right\}}$ és ${\displaystyle \left\{7/3\right\}}$ rendre a és heptagrammák jele.

Mindezek az alakzatok önduálisak.

A szabályos testek Schläfli-szimbólumai: ${\displaystyle \left\{3,3\right\}}$ az önduális tetraéder.

${\displaystyle \left\{3,4\right\}}$ az oktaéder, a megfordított ${\displaystyle \left\{4,3\right\}}$ az oktaéder duálisa, a kocka.

${\displaystyle \left\{3,5\right\}}$ az ikozaéder, a megfordított ${\displaystyle \left\{5,3\right\}}$ az ikozaéder duálisa, a dodekaéder.

${\displaystyle \left\{3,6\right\}}$ a háromszögparketta, az ${\displaystyle \left\{6,3\right\}}$ inverz ennek a duálisa, a hatszögparketta.

${\displaystyle \left\{4,4\right\}}$ az önduális négyzetparketta.

A Kepler-Poinsot-testek Schläfli-szimbólumai: ${\displaystyle \left\{3,5/2\right\}}$ a nagy ikozaédert, az ${\displaystyle \left\{5/2,3\right\}}$ inverziója a duálisát, a nagy csillagdodekaédert írja le.

${\displaystyle \left\{5,5/2\right\}}$ a nagy dodekaédert, az ${\displaystyle \left\{5/2,5\right\}}$ inverzió a duálisát, a kis csillagdodekaédert jellemzi.

${\displaystyle \left\{3,3,3\right\}}$ a pentakhoron,

${\displaystyle \left\{4,3,3\right\}}$ a tesszerakt (négy dimenziós hiperkocka), ${\displaystyle \left\{3,3,4\right\}}$ duálisa pedig a hexadekakhor néven is ismert szabályos 16-cellát jellemzi.

${\displaystyle \left\{3,4,3\right\}}$ az önduális szabályos 24-cella, másként az ikozitetrakhor.

${\displaystyle \left\{5,3,3\right\}}$ a 120-cella, ${\displaystyle \left\{3,3,5\right\}}$ inverziója a szabályos 600-cella.

Magasabb dimenzióban a politóp Schläfli-szimbóluma {p₁, p₂, ..., p_n − 1}, ha lapjainak Schläfli-szimbóluma {p₁,p₂, ..., p_n − 2}, és csúcsalakzatának Schläfli-szimbóluma {p₂,p₃, ..., p_n − 1}.

Egy szabályos politóp lapjának csúcsalakzata és csúcsalakzatának lapja ugyanaz: {p₂,p₃, ..., p_n − 2}.

Négynél magasabb dimenzióban dimenziónként három szabályos politóp van: {3,3,3,...,3} a szimplex; {3,3, ..., 3,4} a keresztpolitóp; és {4,3,3,...,3} a hiperkocka. Konkáv szabályos politópok nincsenek ezekben a dimenziókban.

Az uniform prizmák alacsonyabb dimenziós szabályos politópok Descartes-szorzatai:

• p-gonális prizma: a p.4.4 csúcsalakzatú politóp definiálható, mint { } × {p}, ahol { } a szakasz.
• {p,q}-éderes prizma: a { } × {p,q} szorzat.
• p-q duoprizma: {p} × {q}.

Coxeter a kváziszabályos poliéderekre is kiterjesztette a Schläfli-szimbólumot a csúcsok dimenziójának jelölésével. Ez lett a még általánosabb Coxeter-Dynkin diagram kiindulópontja. Norman Johnson egyszerűsítette a jelölést azzal, hogy a csúcsszimbólumokra bevezette az r prfixet. A t jelölés a legáltalánosabb, és közvetlenül megfelel a Coxeter-Dynkin diagram gyűrűinek. Mindegyik szimbólumnak van alternációja, ahol a Coxeter-Dynkin diagramon a gyűrűket lyukak helyettesítik a h prefixszel. Ez a változtatás csak bizonyos feltételekkel vihető végbe.

Forma	Kiterjesztett Schläfli-szimbólumok			Szimmetria	Coxeter-diagram		Példa: {4,3}
Szabályos	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	{p,q}	t0{p,q}	[p,q] vagy [(p,q,2)]				Kocka
Csonkított	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	t{p,q}	t0,1{p,q}					Csonkított kocka
Bicsonkítás (Csonkított duális)	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	2t{p,q}	t1,2{p,q}					Csonkított oktaéder
Rektifikált (Kváziszabályos)	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	r{p,q}	t1{p,q}					Kuboktaéder
Birektifikáció (Szabályos duális)	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	2r{p,q}	t2{p,q}					Oktaéder
Cantellated (A rektifikált rektifikáltja)	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	rr{p,q}	t0,2{p,q}					Rombikuboktaéder
Élcsonkított (A csonkított rektifikáltja)	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	tr{p,q}	t0,1,2{p,q}					Csonkított kuboktaéder
Alternációk
Alternált szabályos (p páros)	${\displaystyle h{\begin{Bmatrix}p,q\end{Bmatrix}}}$	h{p,q}	ht0{p,q}	[1+,p,q]				Demikocka (Tetraéder)
Snub szabályos (q páros)	${\displaystyle s{\begin{Bmatrix}p,q\end{Bmatrix}}}$	s{p,q}	ht0,1{p,q}	[p+,q]
Snub duális szabály (p páros)	${\displaystyle s{\begin{Bmatrix}q,p\end{Bmatrix}}}$	s{q,p}	ht1,2{p,q}	[p,q+]				Snub oktaéder (Ikozaéder)
Alternált duális szabályos (q páros)	${\displaystyle h{\begin{Bmatrix}q,p\end{Bmatrix}}}$	h{q,p}	ht2{p,q}	[p,q,1+]
Alternált rektifkált (p és q is páros)	${\displaystyle h{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hr{p,q}	ht1{p,q}	[p,1+,q]
Alternált rektifikált rektifikált (p és q is páros)	${\displaystyle hr{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hrr{p,q}	ht0,2{p,q}	[(p,q,2+)]
Quarter (p és q is páros)	${\displaystyle q{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	q{p,q}	ht0ht2{p,q}	[1+,p,q,1+]
Snub rektifikált Snub kváziszabályos	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	sr{p,q}	ht0,1,2{p,q}	[p,q]+				Snub kuboktaéder (Snub kocka)

Linear families

Forma	Kiterjesztett Schläfli-szimbólum			Coxeter-diagram		Példa, {4,3,3}
Szabályos	${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	{p,q,r}	t0{p,q,r}				Tesszerakt
Csonkított	${\displaystyle t{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	t{p,q,r}	t0,1{p,q,r}				Csonkított tesszerakt
Rektifikált	${\displaystyle \left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	r{p,q,r}	t1{p,q,r}				Rektifikált tesszerakt	=
Bicsonkított		2t{p,q,r}	t1,2{p,q,r}				Bicsonkított tesszerakt
Birektifikált (rektifikált duális)	${\displaystyle \left\{{\begin{array}{l}q,p\\r\end{array}}\right\}}$	2r{p,q,r} = r{r,q,p}	t2{p,q,r}				Rektifikált 16-cella	=
Tricsonkított (Csonkított duális)	${\displaystyle t{\begin{Bmatrix}r,q,p\end{Bmatrix}}}$	3t{p,q,r} = t{r,q,p}	t2,3{p,q,r}				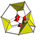Bicsonkított tesszerakt
Trirektifikált (Dual)	${\displaystyle {\begin{Bmatrix}r,q,p\end{Bmatrix}}}$	3r{p,q,r} = {r,q,p}	t3{p,q,r} = {r,q,p}				16-cella
Cantellált	${\displaystyle r\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	rr{p,q,r}	t0,2{p,q,r}				Cantellált tesszerakt	=
Élcsonkított	${\displaystyle t\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	tr{p,q,r}	t0,1,2{p,q,r}				Élcsonkított tesszerakt	=
Runcinált (kiterjesztett)	${\displaystyle e{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	e{p,q,r}	t0,3{p,q,r}				Runcinált tesszerakt
Runcicsonkított			t0,1,3{p,q,r}				Runcicsonkított tesszerakt
Omnicsonkított			t0,1,2,3{p,q,r}				Omnicsonkított tesszerakt
Alternációk
Fél p páros	${\displaystyle h{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	h{p,q,r}	ht0{p,q,r}				16-cella
Negyed p és r páros	${\displaystyle q{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	q{p,q,r}	ht0ht3{p,q,r}
Snub q páros	${\displaystyle s{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	s{p,q,r}	ht0,1{p,q,r}				Snub 24-cella
Snub rectifikált r páros	${\displaystyle s\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	sr{p,q,r}	ht0,1,2{p,q,r}				Snub 24-cella	=
Alternált omnicsonkítás			ht0,1,2,3{p,q,r}				Nagy duoantiprizma

Bifurkáló családok

Forma	Kiterjesztett Schläfli-szimbólum			Coxeter-diagram		Példák
Kváziszabályos	${\displaystyle \left\{p,{q \atop q}\right\}}$	{p,q1,1}	t0{p,q1,1}				16-cella
Csonkított	${\displaystyle t\left\{p,{q \atop q}\right\}}$	t{p,q1,1}	t0,1{p,q1,1}				Csonkított 16-cella
Rektifikált	${\displaystyle \left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	r{p,q1,1}	t1{p,q1,1}				24-cella
Cantellált	${\displaystyle r\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	rr{p,q1,1}	t0,2,3{p,q1,1}				Cantellált 16-cella
Élcsonkított	${\displaystyle t\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	tr{p,q1,1}	t0,1,2,3{p,q1,1}				Élcsonkított 16-cella
Snub rectifikált	${\displaystyle s\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	sr{p,q1,1}	ht0,1,2,3{p,q1,1}				Snub 24-cella
Kváziszabályos	${\displaystyle \left\{r,{p \atop q}\right\}}$	{r,/q\,p}	t0{r,/q\,p}
Csonkított	${\displaystyle t\left\{r,{p \atop q}\right\}}$	t{r,/q\,p}	t0,1{r,/q\,p}
Rektifikált	${\displaystyle \left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	r{r,/q\,p}	t1{r,/q\,p}
Cantellált	${\displaystyle r\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	rr{r,/q\,p}	t0,2,3{r,/q\,p}
Élcsonkított	${\displaystyle t\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	tr{r,/q\,p}	t0,1,2,3{r,/q\,p}
snub rektifikált	${\displaystyle s\left\{{\begin{array}{l}p\\q\\r\end{array}}\right\}}$	sr{p,/q,\r}	ht0,1,2,3{p,/q\,r}

• Coxeter: Regular Polytopes (pp. 14, 69, 149) [1]
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

• Ez a szócikk részben vagy egészben a Schläfli-Symbol című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben a Schläfli symbol című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.