Permutáció
|
Read other articles:

Steven PinkerPinker pada tahun 2011LahirSteven Arthur Pinker18 September 1954 (umur 69)Montreal, Quebec, KanadaTempat tinggalAmerika SerikatWarga negaraKanadaAlmamaterDawson College,Universitas McGill,Universitas HarvardDikenal atasHow the Mind Works, The Blank SlateSuami/istriNancy Etcoff (1980–1992; cerai)Ilavenil Subbiah (1995–?; cerai)Rebecca Goldstein (?-sekarang)PenghargaanTroland Award (1993, United States National Academy of Sciences),Henry Dale Prize (2004, Royal Institutio...

Pakta TripartitPenandatanganan Pakta Tripartit. Dari kiri ke kanan, Saburo Kurusu, Galeazzo Ciano, dan Adolf Hitler.JenisPakta aliansi militerDitandatangani27 September 1940LokasiBerlin, JermanPenanda tanganOrisinil Jerman Italia JepangSubsekwen Hungaria Rumania Slovakia Bulgaria Yugoslavia (selama dua hari) Kroasia Pakta Tripartit (bahasa Jerman: Dreimächtepakt, bahasa Italia: Patto tripartito, bahasa Jepang: Nichidokui sangoku gunji dōmei (日�...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Jean-Baptiste Lully fils – news · newspapers · books · scholar · JSTOR (August 2011) This article...

4th Chief Minister of Uttarakhand This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: B. C. Khanduri – news · newspapers · books · scholar · JSTOR (January 2008) (Learn how and when to remove this t...

Questa voce sull'argomento cestisti canadesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Nickeil Alexander-Walker Nickeil Alexander-Walker, 2023 Nazionalità Canada Altezza 196 cm Peso 93 kg Pallacanestro Ruolo Guardia Squadra Minnesota T'wolves Carriera Giovanili Vaughan Secondary SchoolSt. Louis Christian AcademyHamilton Heights Christian Academy2017-2019 Virg. Tech Hokies Squadr...

Frankfurt Germany TempleNumber41Dedication28 August 1987, by Ezra Taft BensonSite5.6 acres (2.3 ha)Floor area32,895 sq ft (3,056.0 m2)Height82 ft (25 m)Official website • News & imagesChurch chronology ←Denver Colorado Temple Frankfurt Germany Temple →Portland Oregon Temple Additional informationAnnounced1 April 1981, by Spencer W. KimballGroundbreaking1 July 1985, by Gordon B. HinckleyOpen house29 July 29 - 8 August 1987; 13-28 September 2019Reded...

Osteopathic medical school of Liberty University Liberty University College of Osteopathic MedicineTypePrivate medical school Non-profitEstablished2014AffiliationLiberty UniversityDeanJoseph R. Johnson, DOLocationLynchburg, Virginia, USANicknameLUCOMWebsitewww.liberty.edu/lucom/ Liberty University's College of Osteopathic Medicine Liberty University College of Osteopathic Medicine (LUCOM) is a private graduate medical school located in Lynchburg, Virginia. It is one of the seventeen colleges ...

Assassin's Creed NexusLogo officiel du jeu.Développeur Red Storm EntertainmentÉditeur UbisoftDate de sortie INT : 16 novembre 2023 Franchise Assassin's CreedGenre Action-aventure, infiltrationMode de jeu SoloPlate-forme Casque(s) de réalité virtuelle :Meta Quest 2, Meta Quest Pro, Meta Quest 3Langue MultilingueSite web www.ubisoft.com/en-us/game/assassins-creed/nexus-vrmodifier - modifier le code - modifier Wikidata Assassin's Creed Nexus est un jeu vidéo d'action-aventure et d...
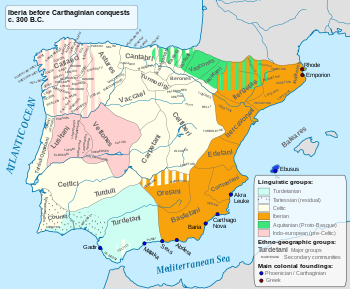
The Iberian Peninsula in the 3rd century BC. The Turmodigi were a pre-Roman ancient people, later mixed with the Celts[1] people of northern Spain who occupied the area within the Arlanzón and Arlanza river valleys in the 2nd Iron Age. Origins The ancestors of the Turmodigi arrived to the Iberian Peninsula in the wake of the earlier Autrigones-Belgae migration at the 4th Century BC, which settled in the area between the Arlanzón and Arlanza rivers.[2][1] The neighbo...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

بورشتين (بالأوكرانية: Буршти́н) بورشتين بورشتين تاريخ التأسيس 1554 تقسيم إداري البلد أوكرانيا [1] التقسيم الأعلى إيفانو فرانكيفسك أوبلاست (11 مارس 2014–) خصائص جغرافية إحداثيات 49°15′36″N 24°38′06″E / 49.26°N 24.635°E / 49.26; 24.635 [2] المساحة 32.71 كيلو...

فريولي علم شعار الإحداثيات 46°09′59″N 13°00′00″E / 46.166388888889°N 13°E / 46.166388888889; 13 تقسيم إداري البلد إيطاليا[2][1] التقسيم الأعلى فريولي فينيتسيا جوليا خصائص جغرافية المساحة 8.240 كيلومتر مربع رمز جيونيمز 3165071 الجوائز ميدالية ا�...

English Civil War soldier and noted angler/author (1613–1687) For the American politician in Delaware, see Robert Venables Sr. Robert VenablesMap of Jamaica, captured by Venables during the 1655 Western DesignGovernor of ChesterIn officeApril 1660 – July 1660Parliamentarian Governor of LiverpoolIn officeJanuary 1647 – August 1649 Personal detailsBorn1613Antrobus, CheshireDied10 December 1687 (aged 73–74)Wincham, CheshireMilitary serviceYears of service1...

Ненасы́щенные жиры́ — триглицериды жирных кислот, в молекулы которых входят остатки ненасыщенных жирных кислот — кислот, в молекулах которых имеется по меньшей мере одна двойная ковалентная связь между атомами углерода. В этом их отличие от насыщенных жирных кис�...

2005 German federal election ← 2002 18 September 2005 (2005-09-18) 2009 → ← outgoing memberselected members →All 614 seats in the Bundestag, including 16 overhang seats308 seats needed for a majorityRegistered61,870,711 0.7%Turnout48,044,134 (77.7%) 1.4pp First party Second party Third party Candidate Angela Merkel Gerhard Schröder Guido Westerwelle Party CDU/CSU SPD FDP Last election 38.5%, 248 seats 38.5%, 251 s...

توأمة مدنمعلومات عامةصنف فرعي من تعاون تعديل - تعديل مصدري - تعديل ويكي بيانات توأمة المدن هو أساسا الاتفاق بين مدينتين على التعاون في مختلف المجالات والأمور التي تعني التجمعات السكنية المدنية.[1][2][3] نبذة ملف:Los Angeles City Hall with sister cities 2006pg|تصغير|مَعلم في لوس أنجلوس|...

Łużyce redirects here. For the part of the Polish village of Dziecinów, Otwock County, see Łużyce, Otwock County. Sorbia redirects here. Not to be confused with Serbia. For the genus, see Sorbia (beetle). Historical regionLusatia Upper Sorbian: ŁužicaLower Sorbian: Łužyca‹See Tfd›German: LausitzPolish: ŁużyceCzech: LužiceHistorical regionCoordinates: 51°32′42.2351″N 14°43′34.1040″E / 51.545065306°N 14.726140000°E / 51.545065306; 14.726140000...

Jewish high court convened by Napoleon This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Grand Sanhedrin – news · newspapers · books · scholar · JSTOR (October 2014) (Learn how and when to remove this message) Contemporary illustration of the Grand Sanhedrin by Michel François Damane Demartrais The Grand Sanh...
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 静岡朝日テレビ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2014年5月) この記事で示されている出典について、該�...

Variety hits radio station in Warrensburg, New York WLGRWarrensburg, New YorkBroadcast areaGlens Falls, New YorkFrequency93.5 MHzBranding93.5 Lake FMProgrammingFormatClassic hitsOwnershipOwnerLoud Media LLC(Loud Media LLC)Sister stationsWSSV, WABYHistoryFirst air date2007 (as WSLP at 93.3)Former call signsWSLP (2006–2021)WPLA (2021)Former frequencies93.3 MHz (2007–2021)Call sign meaningLake George RadioTechnical information[1]Licensing authorityFCCFacility ID165944ClassAERP120 wat...





















