Ohm törvénye
|
Read other articles:

العلاقات الشمال مقدونية اللبنانية شمال مقدونيا لبنان شمال مقدونيا لبنان تعديل مصدري - تعديل العلاقات الشمال مقدونية اللبنانية هي العلاقات الثنائية التي تجمع بين شمال مقدونيا ولبنان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجع�...

Protected wilderness area in California, United States Otay Mountain WildernessIUCN category V (protected landscape/seascape)BLM sign on Otay Mountain Truck TrailLocation in CaliforniaLocationSan Diego County, United StatesNearest cityOtay MesaCoordinates32°35′40″N 116°50′40″W / 32.59444°N 116.84444°W / 32.59444; -116.84444Area16,885 acres (6,833 ha)[1]Established1999 (1999)Governing bodyBureau of Land Management[1][2...

American football player and coach (1890–1945) A. G. ScanlanBiographical detailsBorn(1890-08-16)August 16, 1890Chicago, Illinois, U.S.DiedJuly 8, 1945(1945-07-08) (aged 54)Chicago, Illinois, U.S.Playing career1912–1913Chicago Coaching career (HC unless noted)1918–1920Purdue Head coaching recordOverall7–12–1Accomplishments and honorsChampionships1 Big Ten (1918) Arthur Garrett Butch Scanlan (August 16, 1890 – July 8, 1945) was an American football coach. He served as the head ...

Duchess consort of Saxe-Coburg-Saalfeld Sophie AntoinetteDuchess consort of Saxe-Coburg-SaalfeldTenure16 September 1764 – 8 September 1800Born(1724-01-13)13 January 1724WolfenbüttelDied17 May 1802(1802-05-17) (aged 78)CoburgSpouse Ernest Frederick, Duke of Saxe-Coburg-Saalfeld (m. 1749; died 1800)IssueFrancis Prince Karl Wilhelm Princess Fredericka Princess Caroline Prince Ludwig Karl Prince Ferdinand August Prince FrederickHouseHous...

This is the talk page for discussing WikiProject Pharmacology and anything related to its purposes and tasks. Put new text under old text. Click here to start a new topic. New to Wikipedia? Welcome! Learn to edit; get help. Assume good faith Be polite and avoid personal attacks Be welcoming to newcomers Seek dispute resolution if needed ShortcutWT:PHARM Archives: Index, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17Auto-archiving period: 90 days Pharmacology Project‑classThis...

Tennis tournament2022 Estoril OpenDate25 April – 1 MayEdition7thCategoryATP Tour 250Draw28S / 16DPrize money€534,555SurfaceClay / outdoorLocationCascais, PortugalVenueClube de Ténis do EstorilChampionsSingles Sebastián BáezDoubles Nuno Borges / Francisco Cabral ← 2021 · Estoril Open · 2023 → The 2022 Estoril Open was a men's tennis tournament played on outdoor clay courts. It was the 7th edition of the tournament and part of the ATP Tour 250 serie...
Suburb of Melbourne, Victoria, AustraliaStrathmoreMelbourne, VictoriaStrathmoreCoordinates37°44′02″S 144°55′16″E / 37.734°S 144.921°E / -37.734; 144.921Population8,980 (2021 census)[1] • Density1,321/km2 (3,420/sq mi)Postcode(s)3041Elevation36 m (118 ft)Area6.8 km2 (2.6 sq mi)Location10 km (6 mi) from MelbourneLGA(s)City of Moonee ValleyState electorate(s)EssendonFederal division(s)Maribyrnon...
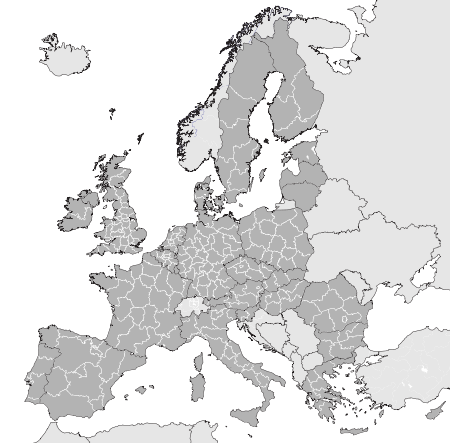
La nomenclatura delle unità territoriali statistiche, in acronimo NUTS (dal francese: Nomenclature des unités territoriales statistiques) identifica la ripartizione del territorio dell'Unione europea a fini statistici. Ideata dall'Eurostat nel 1988 tenendo come riferimento di base l'unità amministrativa locale, da allora è la principale regola per la redistribuzione territoriale dei fondi strutturali della UE, fornendo uno schema unico di ripartizione geografica, a prescindere dalle dimen...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Fratellanza Sportiva Sestrese Calcio 1919. Polisportiva Manlio CavagnaroStagione 1938-1939Sport calcio Squadra Sestrese Allenatore Francesco Parodi Presidente Aristide D'Avanzo Serie C2º posto nel girone D. Coppa ItaliaPrimo turno eliminatorio. StadioCampo Sport...

Disambiguazione – Se stai cercando Corte internazionale di Giustizia, vedi Corte internazionale di giustizia. Corte penale internazionale(FR) Cour pénale internationale(EN) International Criminal Court Logo dell'ICC-CPI La sede della Corte penale internazionale AbbreviazioneICC-CPI TipoTribunale per crimini internazionali Fondazione1º luglio 2002 Sede centrale L'Aia Area di azione124 Paesi Presidente Piotr Hofmański Lingue ufficialiInglese, francese, arabo, cinese, russo...

United States historic placeNew York Public LibraryU.S. National Register of Historic PlacesNYC Landmark No. 0298 Harry Belafonte 115th Street Library, March 2009Location203 W. 115th St., New York, New YorkCoordinates40°48′10″N 73°57′14″W / 40.80278°N 73.95389°W / 40.80278; -73.95389Arealess than one acreBuilt1907ArchitectMcKim, Mead & WhiteArchitectural styleLate 19th And 20th Century Revivals, Neo Italian RenaissanceNRHP reference&...

Political party in Croatia Croatian Peasant Party Hrvatska seljačka strankaAbbreviationHSSPresidentKrešo BeljakFounderStjepan RadićFounded22 December 1904 (1904-12-22) (historical party)15 December 1989 (1989-12-15) (modern party)[1]HeadquartersZagrebMembership (2022)11,421 [2]IdeologyAgrarianism[3][4]Social liberalism[5]Liberalism[6]Green politics[7]Republicanism[6]Pro-Europeanism[4][...

Election 1982 Oregon gubernatorial election ← 1978 November 2, 1982 1986 → Nominee Victor Atiyeh Ted Kulongoski Party Republican Democratic Popular vote 639,841 374,316 Percentage 61.4% 35.9% County resultsAtiyeh: 50–60% 60–70% 70–80% Governor before election Victor Atiyeh Republican Elected Governor Victor Atiyeh Republican Elections in Oregon Federal government P...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Aerial service branch of the Indian Armed Forces Indian Air ForceBadge of the Indian Air ForceFounded26 January 1950; 74 years ago (1950-01-26) (as current service) 8 October 1932; 91 years ago (1932-10-08) (as Royal Indian Air Force) Country IndiaTypeAir forceRoleAerial warfareSize170,576 active personnel[1] 140,000 reserve personnel[2] Approx 1926+ aircraft[3][4]Part of Indian Armed ForcesHeadquartersIntegrat...

See also: Demographics of Gibraltar Languages of GibraltarOne of the many bilingual signs found in the Gibraltar Nature Reserve, printed in both English and Spanish.OfficialEnglishRecognisedSpanishMainEnglishVernacularLlanitoMinorityMaghrebi Arabic, Sindhi, Hindi, Maltese, HebrewSignedBritish Sign LanguageKeyboard layoutBritish (QWERTY) Part of a series on theCulture of Gibraltar History People Genoese Jews Maltese Languages English Llanito Andalusian Spanish Cuisine Religion Roman Cath...

Para el abogado y juez argentino, véase Enrique Santiago Petracchi. Enrique Santiago Romero Secretario de Estado para la Agenda 2030 31 de marzo de 2021-27 de julio de 2022Monarca Felipe VIPresidente Pedro SánchezPredecesora Ione BelarraSucesora Lilith Verstrynge Secretario general del Partido Comunista de España Actualmente en el cargo Desde el 8 de abril de 2018Predecesor José Luis Centella Secretario general de la Unión de Juventudes Comunistas de España 1990-1993Predecesor Manuel J...

中共八大会场。 中国共产党第八次全国代表大会于1956年9月15日至27日在北京召开。出席大会的正式代表1026人,候补代表86人,代表当时全国1073万名党员。在代表大会预备会议期间,由八大各代表团自由提出中央委员、中央候补委员候选人;随后根据第七届中央委员会的决定,由第七届中央政治局和各代表团团长、副团长对于各代表团提出的名单作了研究和讨论,提出了第一...

全椒县县全椒县的地理位置坐标:32°05′42″N 118°15′52″E / 32.09492°N 118.26432°E / 32.09492; 118.26432国家 中华人民共和国隶属行政区安徽省滁州市面积 • 总计1,568.36 平方公里(605.55 平方英里) 人口(2020) • 總計39.56万人时区北京时间(UTC+8)郵政編碼239500行政区划代码341124 全椒县位于中国安徽省东部,是滁州市下辖的一个县。...

French dynastic war from 1407 to 1435 Armagnac–Burgundian Civil WarPart of the Hundred Years' WarThe Cabochien revolt in 1413Date23 November 1407 – 21 September 1435 (27 years, 9 months, 4 weeks and 1 day)LocationKingdom of FranceResult Treaty of ArrasArmagnac and Burgundian reconciliationBelligerents Armagnac party Burgundian party EnglandCommanders and leaders Louis of Orléans † Charles of Orléans Bernard of Armagnac † Charles VII of Fran...






















