NMR-spektroszkópia
|
Read other articles:

ميّز عن معلم تذكاري. نصب تذكاري النصب أو النصب التذكاري هو بناء أو موقع أو تمثال شيد لتخليد ذكرى شخص أو حادثة.[1][2] والنصب القومية هي أماكن لها أهمية تاريخية وعلمية، والمشاهد الخلابة التي تحافظ عليها الحكومة، باعتبارها ممتلكات شعبية. وتتضمّن هذه المباني القصو...
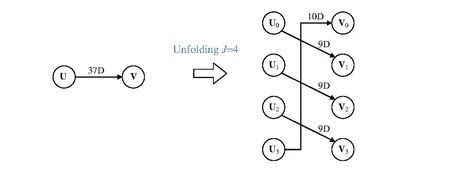
Unfolding is a transformation technique of duplicating the functional blocks to increase the throughput of the DSP program in such a way that preserves its functional behavior at its outputs. Unfolding was first proposed by Keshab K. Parhi and David G. Messerschmitt in 1989.[1][2] Unfolding in general program is as known as Loop unrolling. Unfolding has applications in designing high-speed and low-power ASIC architectures. One application is to unfold the program to reveal hid...

هذه المقالة عن ماري وارد. لمعانٍ أخرى، طالع وارد (توضيح). ماري وارد (بالإنجليزية: Mary Ward) معلومات شخصية الميلاد 27 أبريل 1827(1827-04-27)مقاطعة أوفالي الوفاة 31 أغسطس 1869 (42 سنة) سبب الوفاة حادث سيارة[1] الحياة العملية المهنة عالمة فلك[2]، ومؤلفة[2]، وعا...

Cet article concerne le quotidien Le Vélo. Pour le service de vélo en libre service marseillais, voir Le vélo (vélopartage). Le Vélo Pays France Langue Français Fondateur Pierre Giffard Date de fondation 1er décembre 1892 Date du dernier numéro 20 novembre 1904 Rédacteur en chef Paul RousseauGaston de Pawlowski modifier Le Vélo est un quotidien français spécialisé dans le sport, qui parut en France à la fin du XIXe siècle et au début du XXe siècle. C...

Sayur lodehJenisSayur berkuahSajianHidangan utamaTempat asalIndonesiaDaerahJawa, Seluruh NusantaraSuhu penyajianPanas, atau suhu ruangBahan utamaSantan, sayur (nangka, terong, labu siam, melinjo, kacang panjang, tahu, tempe), ayam atau kaldu sapiSunting kotak info • L • BBantuan penggunaan templat ini Media: Sayur lodeh Resep bumbu lodeh Sayur lodeh (Jawa: ꦗꦔꦤ꧀ꦭꦺꦴꦝꦺꦃ, translit. Jangan lodhèh) adalah masakan sayur yang berkuah santan kha...

Pour les articles homonymes, voir Cairo. Cet article est une ébauche concernant une localité de Géorgie (États-Unis). Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Cairo La cour de justice du comté. Administration Pays États-Unis État Géorgie Comté Grady Type de localité City Code ZIP 31728, 39827, 39828 Code FIPS 13-12400 GNIS 0354934 Indicatif(s) téléphonique(s) local (locaux) 229 Démographie Po...

Governorate of Iraq Governorate in Tikrit, IraqSaladin Governorate صلاح الدينGovernorateŞalāḩ ad Dīn FlagCoordinates: 34°27′N 43°35′E / 34.450°N 43.583°E / 34.450; 43.583CountryIraqCapitalTikritGovernorAmmar Jabr Al-JubouriArea • Total24,751 km2 (9,556 sq mi)Population (2018) • Total1,595,235Official language(s)ArabicHDI (2021)0.692[1]medium The Saladin, Salah ad Din or Salah Al-Din Governorate (...

Komando Resor Militer 073/MakutaramaLambang Korem 073/MakutaramaDibentuk1 September 1961Negara IndonesiaCabangTNI Angkatan DaratTipe unitKomando Resor MiliterPeranSatuan TeritorialBagian dariKodam IV/DiponegoroMakoremSalatigaJulukanKorem 073/MktPelindungTentara Nasional IndonesiaMotoBekti Tata Gapuraning BuwanaBaret H I J A U Situs webkorem073mkt.tni-ad.mil.idTokohKomandanKolonel Inf Purnomosidi, S.I.P., M.A.P.Kepala StafLetkol Kav Indarto Komando Resor Militer 073/Makutarama, disin...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

هذه المقالة عن ولاية سوق أهراس. لمعانٍ أخرى، طالع سوق أهراس. ولاية سوق أهراس ولاية سوق أهراس ولاية سوق أهراس الإدارة عاصمة الولاية سوق أهراس رمز الولاية 41 الموقع الرسمي ولاية سوق أهراس بعض الأرقام مساحة 4541 كم² (30) تعداد السكان 592,127 نسمة (33) إحصاء سنة 2023 م كثافة 130.79 نسمة/�...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أغسطس 2020) هذه الص...

American actor (1917–2002) For the ice hockey player, see Brad Dexter (ice hockey). Brad DexterDexter in Heldorado (1946)BornBoris Michel Soso(1917-04-09)April 9, 1917Goldfield, Nevada, U.S.DiedDecember 12, 2002(2002-12-12) (aged 85)Rancho Mirage, California, U.S.Resting placeDesert Memorial Park, Cathedral City, California, U.S.Other namesBoris MilanovichBoris Mitchell SosoBarry MitchellOccupation(s)Actor, producerYears active1944–1988Spouses Peggy Lee &...

United States Army officer (1831–1863) Stephen Hinsdale WeedBorn(1831-11-17)November 17, 1831Potsdam, New YorkDiedJuly 2, 1863(1863-07-02) (aged 31)Gettysburg, PennsylvaniaPlace of burialMoravian Cemetery, New Dorp, Staten Island, New YorkAllegianceUnited States of AmericaUnionService/branchUnited States ArmyUnion ArmyYears of service1854–1863Rank Brigadier General[1]Commands held5th U.S. Light Artillery, Battery IBattles/warsIndian WarsSeminole WarsUtah WarAmerican Civi...

Overview of the transport in Nigeria Nigeria’s transport network has expanded in recent years to accommodate a growing population. The transport and storage sector was valued at N2.6trn ($6.9bn) in current basic prices in 2020, down from N3trn ($8bn) in 2019, according to the National Bureau of Statistics (NBS). This was reflected in a lower contribution to GDP, at 1.8% in the fourth quarter of 2020, down from 2.1% during the same period the previous year but higher than the 0.8% recorded i...

Bowel dysfunction Medical conditionConstipationOther namesCostiveness,[1] dyschezia[2]Constipation in a young child seen on X-ray. Circles represent areas of fecal matter (stool is white surrounded by black bowel gas).SpecialtyGastroenterologySymptomsInfrequent or hard to pass bowel movements, abdominal pain, bloating[2][3]ComplicationsHemorrhoids, anal fissure, fecal impaction[4]CausesSlow movement of stool within the colon, irritable bowel syndrome, c...

IWGP Tag Team ChampionshipSabuk IWGP Tag Team ChampionshipInformasiJuara saat iniBishamon (Hirooki Goto dan Yoshi-Hashi)Tanggal dimenangkan4 Juni 2023Tanggal dibentuk12 Desember 1985[1]PromotorNew Japan Pro-Wrestling (NJPW)Nama lain IWGP Heavyweight Tag Team Championship (nama yang digunakan oleh AEW) IWGP World Tag Team Championship (nama yang digunakan oleh ROH dan TNA) StatistikPemegang pertamaKengo Kimura & Tatsumi FujinamiPemegang terbanyak(sebagai tim)Guerrillas of Destiny (...

Form of non-verbal/non-vocal communication For gestures in computing, see Gesture recognition and Pointing device gesture. For other uses, see Gesture (disambiguation). Gestures and Talking with your hands redirect here. For the rock group, see The Gestures. For the form of language, see Sign language. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations...
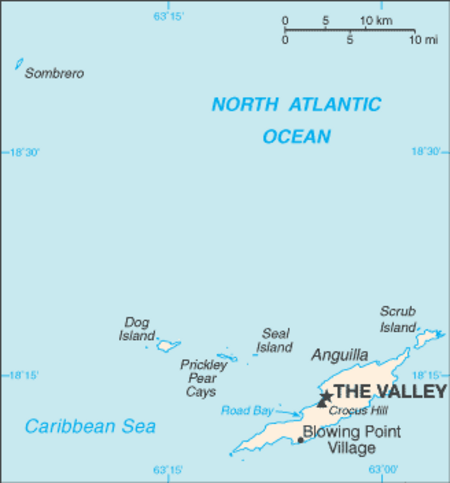
Prickly Pear CaysGli isolotti fotografati dal mare.Geografia fisicaLocalizzazioneOceano Atlantico, Mar dei Caraibi Coordinate18°15′50″N 63°10′25″W18°15′50″N, 63°10′25″W Geografia politicaStato Regno Unito Territorio d'oltremare Anguilla DemografiaAbitanti0 (-) Cartografia Prickly Pear Cays voci di isole del Regno Unito presenti su Wikipedia Le Prickly Pear Cays, conosciute anche come Prickley Pear Cays, (traducibile in italiano con isole dei fichi d'india) sono d...

まつかた ひろき松方 弘樹 『映画情報』1962年4月号(国際情報社)より本名 目黒 浩樹(めぐろ こうじゅ)生年月日 (1942-07-23) 1942年7月23日没年月日 (2017-01-21) 2017年1月21日(74歳没)出身地 日本・東京府東京市王子区(現・東京都北区)赤羽台死没地 日本・東京都身長 173 cm血液型 A型職業 俳優・映画監督・映画プロデューサージャンル 映画・テレビドラマ・時代劇オリジ...

果たし得ていない約束―私の中の二十五年作者 三島由紀夫国 日本言語 日本語ジャンル 随筆、評論発表形態 新聞掲載初出情報初出 『サンケイ新聞』(夕刊)1970年7月7日号刊本情報収録 評論集『蘭陵王―三島由紀夫 1967.1 - 1970.11』出版元 新潮社出版年月日 1971年5月6日装幀 増田幸右 ウィキポータル 文学 ポータル 書物テンプレートを表示 『果たし得ていない約束―私の中�...




















![{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4609400985a74e43afdf85f79eb7b383d0638256)





