Négyes számrendszer
|
Read other articles:

UgetsuPosterSutradaraKenji MizoguchiProduserMasaichi NagataDitulis olehMatsutarō KawaguchiAkinari UedaYoshikata YodaPemeranMasayuki MoriMachiko KyōKinuyo TanakaPenata musikFumio HayasakaDistributorDaieiTanggal rilis26 Maret 1953Durasi94 minNegaraJepangBahasaJepangIMDbInformasi di IMDbAMGProfil All Movie Guide Ugetsu (雨月物語code: ja is deprecated , Ugetsu monogatari) adalah film tahun 1953 oleh sutradara Kenji Mizoguchi. Film ini dibintangi Masayuki Mori dan Machiko Kyō, diilham...

Hannah LamdanLahir5 Januari 1905Tempat lahirShirivtsi, Kekaisaran RusiaTahun aliyah1926Meninggal dunia10 April 1995 (usai 90)Tempat meninggalHolon, IsraelKnesset1, 2, 3, 4, 5Faksi yang diwakili di Knesset1949–1953Mapam1953–1954Faksi independen Ahdut HaAvoda1954–1965Mapai1965Rafi Hannah Lamdan (bahasa Ibrani: חנה למדן, 5 Januari 1905 – 10 April 1995) adalah seorang politikus Israel. Ia menjabat sebagai anggota Knesset untuk beberapa partai sayap kiri ant...

Ewald BalserLahir(1898-10-05)5 Oktober 1898Elberfeld, JermanMeninggal17 April 1978(1978-04-17) (umur 79)Wina, AustriaPekerjaanPemeranTahun aktif1935–1975 Ewald Balser (5 Oktober 1898 – 17 April 1978) adalah seorang pemeran film asal Jerman. Ia tampil dalam 53 film antara 1935 dan 1975. Ia lahir di Elberfeld, Jerman dan wafat di Wina, Austria.[1] Referensi ^ Ewald Balser. Film Portal. Diakses tanggal 14 June 2019. Pranala luar Wikimedia Commons memili...

Koordinat: 5°03′46″S 119°44′55″E / 5.0627637°S 119.7486639°E / -5.0627637; 119.7486639 LaiyaDesaNegara IndonesiaProvinsiSulawesi SelatanKabupatenMarosKecamatanCenranaKode pos90524Kode Kemendagri73.09.10.2001 Luas63,13 km² tahun 2017Jumlah penduduk2.880 jiwa tahun 2017Kepadatan45,62 jiwa/km² tahun 2017Jumlah RT21Jumlah RW7 Laiya (Ejaan Van Ophuijsen: Laija; Lontara Bugis & Lontara Makassar: ᨒᨕᨗᨐ, transliterasi: Laiya) adalah nama sebuah de...

Halaman ini berisi artikel tentang gugus fungsional organik aril. Untuk artikel lainnya dengan nama yang serupa, lihat ariel (disambiguasi). Fenil merupakan suatu gugus aril paling sederhana, pada gambar ini terikat dengan suatu gugus R. Dalam konteks molekul organik, aril merupakan semua gugus fungsional atau substituen yang berasal dari suatu cincin aromatik, biasanya suatu hidrokarbon aromatik, dapat berupa fenil, naftil, indolil, dan lain sebagainya. (lihat tata nama senyawa kimia).[1...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: National Commissioners Invitational Tournament – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message) The National Commissioners Invitational Tournament was an eight-team postseason men's college basketball tournament ru...

Johann Christian Reil, in un ritratto del 1811 Johann Christian Reil (Rhauderfehn, 20 febbraio 1759 – 22 novembre 1813) è stato uno psichiatra, anatomista e fisiologo tedesco. Tomba di Reil sul Reilberg di Halle (Saale), Germania, l'attuale Bergzoo Halle Indice 1 Biografia 1.1 Morte 2 Note 3 Bibliografia 4 Voci correlate 5 Altri progetti 6 Collegamenti esterni Biografia Fu lui a coniare il termine psichiatria, in tedesco psychiatrie, nel 1808.[1][2] Tra le malattie e le car...

Campionati Internazionali di Sicilia 1989 Sport Tennis Data 25 settembre – 1º ottobre Edizione 10a Superficie Terra rossa Campioni Singolare Franco Davín Doppio Peter Ballauff / Rudiger Haas 1988 1990 I Campionati Internazionali di Sicilia 1989 sono stati un torneo di tennis giocato sulla terra rossa. È stata la 10ª edizione dei Campionati Internazionali di Sicilia, che fanno parte del Nabisco Grand Prix 1989. Si sono giocati a Palermo in Italia, dal 25 settembre al 1º ottobre 1989. I...

Disambiguazione – UMD rimanda qui. Se stai cercando altri significati, vedi UMD (disambigua). Questa voce o sezione sull'argomento informatica è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più pr...
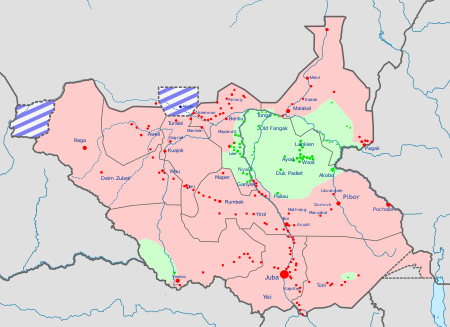
Southern Sudan Civil War Racism in Sudan is a complex matter due to the racial mixture of various populations. Sudanese Arabs are among the 600 ethnic groups who live there, and there are elements within Sudanese society that view black people and blackness with disfavor.[1][2] Sudan is dominated by a light-skinned, Arabic-speaking elite, while black Africans often face oppression and marginalization.[3] Sudan has been in the Arab League since 1956. Skin whitening is r...

Airline alliance Vanilla AllianceLaunch date21 September 2015; 8 years ago (2015-09-21)Full members5Destination airports89Destination countries26Annual passengers (M)2.3[1]Fleet size46ManagementMarie-Joseph Malé, president[2] The Vanilla Alliance (French: Alliance Vanille) is an airline alliance formed in September 2015. The alliance is the fourth largest in the world as of 2018, trailing Oneworld, Star Alliance, and SkyTeam.[3] All of the airlines w...

Cet article ou cette section contient des informations sur des scrutins à venir. Il se peut que ces informations soient de nature spéculative et que leur teneur change considérablement alors que les événements approchent.La dernière modification de cette page a été faite le 6 avril 2024 à 16:03. 2018 Élection présidentielle vénézuélienne de 2024 28 juillet 2024 Nicolas Maduro – PSUV Edmundo González Urrutia – Plateforme unitaire Président du Venezuela Sortant Ni...

American politician (1909–1983) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Erastus Corning 2nd – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) Erastus Corning 2ndMayor Corning in 196972nd Mayor of Albany, New YorkIn officeJanuary 2, 1942 –&#...

Natsumi Abe安倍 なつみGambar langsung Abe Natsumi di Bangkok, Thailand, 2014Lahir安倍 なつみ (Natsumi Abe)10 Agustus 1981 (umur 42)Muroran, Hokkaidō, JepangPekerjaanSingerSuami/istriIkusaburo Yamazaki (m. 2015)Anak1Karier musikGenrePopTahun aktif1997–sekarangLabel Zetima Hachama Artis terkait Morning Musume (1997–2004) Nochiura Natsumi Def.Diva Sakuragumi Kiiro 5 10-nin Matsuri Odoru 11 Salt5 H.P. All Stars Dream Morning Musume (2011–) Mai...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Domestic athletics championship event International athletics championship event2023 New Zealand Track & Field ChampionshipsDates2–5 MarchHost cityWellingtonVenueNewtown Park← 2022 2024 → The 2023 New Zealand Athletics Championships was the national championship in outdoor track and field for New Zealand. It was held from 2–5 March at Newtown Park in Wellington. The 10,000 metres was held separately on 19 November 2022 and The Combined Events Championship (incorporating th...

Australian cricketer Arthur RichardsonPersonal informationBorn(1888-07-24)24 July 1888Clare, South AustraliaDied23 December 1973(1973-12-23) (aged 85)Semaphore, South AustraliaBattingRight-handedBowlingRight-arm off-spinRight-arm mediumInternational information National sideAustraliaTest debut (cap 118)19 December 1924 v EnglandLast Test14 August 1926 v England Domestic team information YearsTeam1918/19–1926/27South Australia1927/28–1929/30Western Austral...

Halaman ini berisi artikel tentang film tahun 1982 berdasarkan novel. Untuk novel aslinya, lihat The Year of Living Dangerously (novel). The Year of Living DangerouslySutradaraPeter WeirProduserJim McElroyDitulis oleh Christopher Koch Peter Weir David Williamson Pemeran Mel Gibson Sigourney Weaver Linda Hunt DistributorMGMTanggal rilis17 Desember 1983Durasi117 menitNegara Australia The Year of Living Dangerously adalah film drama romantik buatan Australia yang menceritakan kisah petualangan s...

Czechoslovak actor You can help expand this article with text translated from the corresponding article in Czech. (January 2011) Click [show] for important translation instructions. View a machine-translated version of the Czech article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into t...

Questa voce sull'argomento missioni spaziali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. STS-36Emblema missione Dati della missioneOperatoreNASA NSSDC ID1990-019A SCN20512 ShuttleAtlantis Lancio28 febbraio 1990, 2:50:22 a.m. EST Luogo lancioRampa 39A Atterraggio4 marzo 1990, 10:08:44 a.m. PST Sito atterraggioEdwards Air Force Base (pista 23) Durata4 giorni, 10 ore, 18 minuti e 22 secondi Proprietà...
