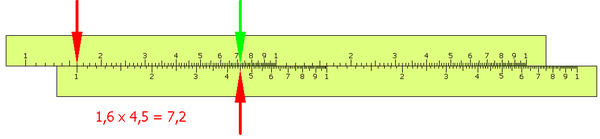
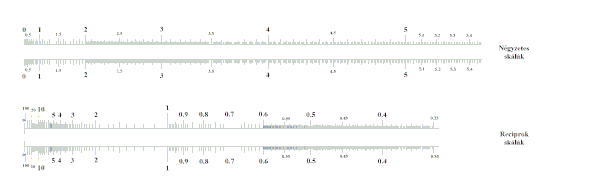
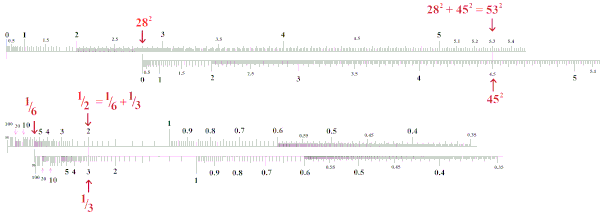
Logarléc
|
Read other articles:

Hippopsis Hippopsis lemniscata Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Hippopsis Hippopsis adalah genus kumbang tanduk panjang yang berasal dari famili Cerambycidae. Genus ini juga merupakan bagian dari ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang dalam genus ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu hidup atau kayu yang telah diteban...

KatedralGereja Katedral Santo Yakobus AgungJerman: Innsbrucker Domcode: de is deprecated Katedral InnsbruckKatedralLokasiInnsbruck, TirolNegaraAustriaDenominasiGereja Katolik RomaSitus webwww.dibk.atSejarahDedikasiSanto Yakobus AgungTanggal konsekrasi1724ArsitekturStatusKatedralStatus fungsionalAktifPeletakan batu pertama12 Mei 1717Selesai1724SpesifikasiLebar bagian tengah gereja17 meter (56 ft)AdministrasiKeuskupanKeuskupan InnsbruckKlerusUskupYang Mulia Mgr. Manfred Scheuer Katedral In...

Bekim FehmiuFehmiu sebagai Ulysses dalam miniseri TV Italia tahun 1968 L'Odissea.Lahir(1936-06-01)1 Juni 1936Sarajevo, Drina Banovina, Kerajaan YugoslaviaMeninggal15 Juni 2010(2010-06-15) (umur 74)Belgrade, SerbiaPekerjaanPemeranTahun aktif1953–1998 Bekim Fehmiu (bahasa Serbia: Беким Фехмију; 1 Juni 1936 – 15 Juni 2010) adalah seorang pemeran teater dan film Yugoslavia berdarah Albania.[1][2][3] Ia adalah pemeran Eropa Timur...

Sexy Boy (Soyokaze ni Yorisotte)Singel oleh Morning Musumedari album Sexy 8 BeatSisi-BChance Chance BoogieDirilis15 Maret 2006 (2006-03-15)FormatCD, DVDDirekam2006GenrePopDurasi11:20LabelZetimaPenciptaTsunkuProduserTsunkuVideo musikSexy Boy (Soyokaze ni Yorisotte) di YouTubeSampul alternatif Sexy Boy (Soyokaze ni Yorisotte) (SEXY BOY 〜そよ風に寄り添って〜code: ja is deprecated ) Adalah singel ke dua puluh sembilan dari grup J-pop Morning Musume. Singel ini dirilis pada 15 Mar...

Tinker Bell and the Legend of the NeverBeastFilm posterSutradaraSteve LoterProduserMakul WigertSkenario Kate Kondell Mark McCorkle Tom Rodgers Robert Schooley Cerita Steve Loter Tom Rodgers BerdasarkanPeter and Wendyoleh J. M. BarriePemeranGinnifer Goodwin Mae Whitman Rosario Dawson Lucy Liu Raven-Symoné Megan HiltyNaratorGrey GriffinPenata musikJoel McNeely[1]SinematograferNavneet VermaPenyuntingMargaret HouPerusahaanproduksiMetro-Goldwyn-Mayer PicturesDistributorParamount Pic...

العلاقات الألمانية السنغافورية ألمانيا سنغافورة ألمانيا سنغافورة تعديل مصدري - تعديل العلاقات الألمانية السنغافورية هي العلاقات الثنائية التي تجمع بين ألمانيا وسنغافورة.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتي�...

Ranj Pillai Ranj Pillai en 2022. Fonctions 10e premier ministre du Yukon En fonction depuis le 14 janvier 2023(1 an, 3 mois et 2 jours) Monarque Charles III Prédécesseur Sandy Silver Chef du Parti libéral du Yukon En fonction depuis le 9 janvier 2023(1 an, 3 mois et 7 jours) Prédécesseur Sandy Silver Député à l'Assemblée législative du Yukon En fonction depuis le 7 novembre 2016(7 ans, 5 mois et 9 jours) Élection 7 novembre 2016 Rééle...

Union state in the American Civil War Union states in the American Civil War California Connecticut Delaware Illinois Indiana Iowa Kansas Maine Maryland Massachusetts Michigan Minnesota Nevada New Hampshire New Jersey New York Ohio Oregon Pennsylvania Rhode Island Vermont West Virginia Wisconsin Dual governments Kentucky Missouri Virginia West Virginia Territories and D.C. Arizona Colorado Dakota District of Columbia Idaho Indian Territory Montana Nebraska New Mexico Utah Washington vte Nevad...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Companion of Muhammad and first Islamic mu'azzin (c.580–640) This article is about the companion of Muhammad. For the Mosque named in his honour, see Rachel's tomb. Bilāl ibn Rabāḥبِلَال بِن رَبَاحBornMarch 5, 580BirthplaceMecca, HejazKnown forbeing the first mu'azzin in Islam history [1][2]OccupationMu'azzin and Secretary of Treasure of The Islamic State of MedinaTitleSayyid al-MuʾaḏḏinDiedMarch 2, 640(640-03-02) (aged 59)FatherRabahMotherHamama...

博里萨夫·约维奇攝於2009年 南斯拉夫社會主義聯邦共和國第12任總統任期1990年5月15日—1991年5月15日总理安特·马尔科维奇前任亚内兹·德尔诺夫舍克继任塞吉多·巴伊拉莫维奇(英语:Sejdo Bajramović) (代任)第12任不结盟运动秘书长任期1990年5月15日—1991年5月15日前任亚内兹·德尔诺夫舍克继任斯捷潘·梅西奇第3任塞尔维亚常驻南斯拉夫社会主义联邦共和国主席团代表任�...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

French submarine 49°48′31.6″N 1°26′42.1″W / 49.808778°N 1.445028°W / 49.808778; -1.445028 Prométhée Prométhée during trials. The 100 mm deck gun had not yet been installed. History France NameProméthée NamesakePrometheus, a Titan god of fire in Greek mythology BuilderArsenal de Cherbourg Laid down10 January 1928 Launched23 October 1930 CommissionedNever commissioned FateSunk on 7 July 1932 General characteristics Class and typeRedoutable-class submari...

فريدريك ليونارد معلومات شخصية الميلاد 12 مارس 1896(1896-03-12)ماونت فيرنون الوفاة 23 يونيو 1960 (64 سنة)لوس أنجلوس مواطنة الولايات المتحدة الحياة العملية المدرسة الأم جامعة شيكاغوجامعة كاليفورنيا، بركلي المهنة فلكي موظف في جامعة كاليفورنيا تعديل مصدري - تعديل ...

Porter-class destroyer For other ships with the same name, see USS Selfridge. USS Selfridge (DD-357) History United States BuilderNew York Shipbuilding Corporation Laid down18 December 1933 Launched18 April 1936 Commissioned25 November 1936 Decommissioned15 October 1945 Stricken1 November 1945 FateSold 20 December 1946 and scrapped General characteristics Class and typePorter-class destroyer Displacement1,850 tons, 2,597 tons full Length381 ft (116 m) Beam36 ft 2 ...
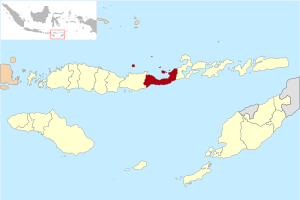
Kabupaten SikkaKabupatenHutan Mata Air di Pegunungan Wairterang LambangJulukan: Kota Tanah SikkaMotto: Dari Tuhan, Kembali ke TuhanPetaKabupaten SikkaPetaTampilkan peta Kepulauan Sunda KecilKabupaten SikkaKabupaten Sikka (Indonesia)Tampilkan peta IndonesiaKoordinat: 8°29′18″S 122°58′26″E / 8.4883°S 122.974°E / -8.4883; 122.974Negara IndonesiaProvinsiNusa Tenggara TimurTanggal berdiri1 Maret 1958Dasar hukumUU nomor 69 tahun 1958Ibu kotaMaumere...

Network of space-tracking stations of the European Space Agency This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: ESTRACK – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) The European Space Tracking (ESTRACK) network consists of a number of ground-based s...

Zona libera da armi nucleari Stati con armi nucleari (Russia, USA, Francia, Cina, Regno Unito, Israele, Pakistan, India, Corea del Nord) Condivisione nucleare (Belgio, Germania, Italia, Paesi Bassi, Turchia e Bielorussia) Non condivisione, ma adesione al TNP Ispezione di un sistema di stoccaggio di armi nucleari degli Stati Uniti nella Volkel Air Base nei Paesi Bassi. Un F-1...
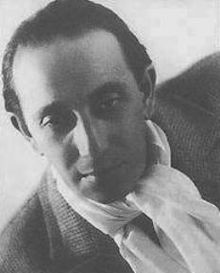
Paul Abraham Paul Abraham (bahasa Hongaria: Ábrahám Pál; 2 November 1892 – 6 Mei 1960) adalah seorang komponis operetta Yahudi-Hungaria yang aktif dari tahun 1928 hingga dasawarsa 1930-an. Karyanya populer di wilayah berbahasa Jerman di Eropa Tengah. Setelah Partai Nazi mulai menguasai Jerman pada tahun 1933, ia pindah ke Amerika Serikat dan menetap di sana hingga tahun 1958.[1] Beberapa karyanya yang terkenal adalah:[1] Viktoria und ihr Husar, 1930 Die ...
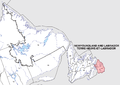
Town in Newfoundland and Labrador, CanadaSt. Mary'sTownSt. Mary'sLocation of St. Mary's in NewfoundlandShow map of NewfoundlandSt. Mary'sSt. Mary's (Canada)Show map of CanadaCoordinates: 46°54′49″N 53°31′54″W / 46.91361°N 53.53167°W / 46.91361; -53.53167[1]CountryCanadaProvinceNewfoundland and LabradorCensus division1Settled1600sIncorporated (town)1966Government • MHASherry Gambin-Walsh (LIB) • MPKen McDonald (LIB)Area ...