Összefüggő komponens (gráfelmélet)
|
Read other articles:

Questa voce o sezione sull'argomento siti archeologici del Messico non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. AzcapotzalcoEmblema della città di AzcapotzalcoCiviltàTepanechi EpocaXIII secolo LocalizzazioneStato Messico Modifica dati su Wikidata · Manuale Azcapotzalco (nella terra delle formiche, dal nahuatl azcatl, formica; postal, terr...
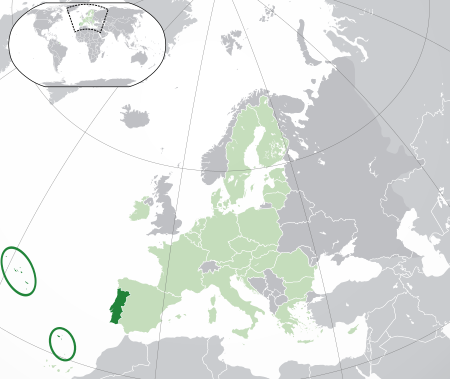
Country in Southwestern Europe For other uses, see Portugal (disambiguation). Portuguese RepublicRepública Portuguesa (Portuguese) Flag Coat of arms Anthem: A PortuguesaThe PortugueseShow globeShow map of the European UnionLocation of Portugal (dark green)– in Europe (green & dark grey)– in the European Union (green)Capitaland largest cityLisbon38°46′N 9°9′W / 38.767°N 9.150°W / 38.767; -9.150Official l...

مزبان - قرية - تقسيم إداري البلد إيران[1] المحافظة محافظة خوزستان المقاطعة إقليم الأحواز قسم الناحية المركزية لمقاطعة الأهواز التقسيم الإداري الإيراني قسم إسماعيلية الريفي إحداثيات 31°04′28″N 48°22′02″E / 31.07444°N 48.36722°E / 31.07444; 48.36722 السكان التعدا�...

Island in Tristan da Cunha archipelago Map of Tristan da Cunha, showing Stoltenhoff Island Stoltenhoff Islandclass=notpageimage| Location of Stoltenhoff Island in the Atlantic Ocean Stoltenhoff Island is a small uninhabited island in the South Atlantic Ocean, part of the Nightingale Islands. It is the smallest of the Nightingale Islands, and is to the northwest of Nightingale Island itself. They are governed as part of Tristan da Cunha, an archipelago and part of the British overseas territor...

Untuk kegunaan lain, lihat Chickasaw (disambiguasi). ChickasawBaris atas: anak muda Chickasaw, Tom Cole, Winchester ColbertBaris tengah: Holmes Colbert, John Herrington, J. D. JamesBaris bawah: Mary Hightower (Shunahoyah), Ashkehenaniew, Annie Guy Daerah dengan populasi signifikan Amerika Serikat (Oklahoma, Mississippi, Louisiana)BahasaInggris, ChickasawAgamaKepercayaan tradisional, Kekristenan (Protestantisme)Kelompok etnik terkaitChoctaw, Muscogee, dan Seminole Chickasaw adalah pendudu...

Stasiun Higashi-Shiroishi東白石駅Stasiun Higashi-ShiroishiLokasiShirakawa-uchioya, Shiroishi-shi, Miyagi-ken 989-1104JepangKoordinat38°02′5.73″N 140°39′4.02″E / 38.0349250°N 140.6511167°E / 38.0349250; 140.6511167Koordinat: 38°02′5.73″N 140°39′4.02″E / 38.0349250°N 140.6511167°E / 38.0349250; 140.6511167Operator JR EastJalur■ Jalur Utama TōhokuLetak311.0 km dari TokyoJumlah peron2 peron sampingJumlah jalur2Informas...

Italian duchy (554 – ca. 752) Duchy of PerugiaDucatus PerusianusDuchy of the Byzantine Empire554 – ca. 752Map of the Exarchate and the Lombard territories around the mid-7th century.CapitalPerugiaHistorical eraMiddle Ages• Establishment under the authority of the Praetorian Prefect of Italy 554• Part of the Exarchate of Ravenna 584• De facto control by the Papacy ca. 752 Today part ofItaly The Duchy of Perugia was a duchy (Latin: ducatus) in the Italian part of the By...

Part of a series on the History of Libya Prehistory Ancient history 3200–146 BC Roman era 146 BC – mid-7C Islamic rule mid-7c–1510 Spanish Tripoli 1510–1530 Hospitaller Tripoli 1530–1551 Ottoman Tripolitania 1551–1911 Italian colonization:Italian Tripolitania and Cyrenaica 1911–1934 Italian Libya 1934–1943 Allied occupation 1943–1951 Kingdom of Libya 1951–1969 Libya under Muammar Gaddafi 1969–2011 First Civil War 2011 National ...

Paris-Le Bourget Vue générale. Localisation Pays France Ville • Le Bourget• Dugny• Bonneuil-en-France• Gonesse Date d'ouverture 1919 Coordonnées 48° 56′ 59″ nord, 2° 25′ 56″ est Superficie 550 ha Altitude 66 m (217 ft) Informations aéronautiques Code IATA LBG Code OACI LFPB Nom cartographique Paris LE BOURGET Type d'aéroport civil à usage restreint Gestionnaire Paris Aéroport Site web gestionnaire Consulter Pistes Direction Longueur Surf...

Perigi BaruKelurahanNegara IndonesiaProvinsiBantenKotaTangerang SelatanKecamatanPondok ArenKodepos15428[1]Kode Kemendagri36.74.03.1009 Kode BPS3674060001 Luas316.826 HaJumlah penduduk12.452 jiwa (2021) Perigi Baru adalah kelurahan di kecamatan Pondok Aren, Tangerang Selatan, Banten, Indonesia. Lurah Perigi Baru saat ini dijabat oleh Lurah ADE HELMI FIRMANSYAH, SE. Kelurahan ini merupakan pemekaran dari Desa Perigi yang menjadi Kelurahan Perigi Lama dan Perigi Baru. Kelurahan ini ...

En mathématiques, et plus précisément en algèbre linéaire, le théorème du rang lie le rang d'une application linéaire et la dimension de son noyau. C'est un corollaire d'un théorème d'isomorphisme. Il peut être interprété par la notion d'indice d'application linéaire. En dimension finie, il permet notamment de caractériser l'inversibilité d'une application linéaire ou d'une matrice par son rang. Le théorème du rang Théorème du rang — Soient E et F deux esp...

密西西比州 哥伦布城市綽號:Possum Town哥伦布位于密西西比州的位置坐标:33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里(57.8 平方公里) • 陸地21.4 平方英里(55.5 平方公里) • ...

Не плутати з Департамент військової контррозвідки Служби безпеки України. Не плутати з Департамент контррозвідувального захисту інтересів держави у сфері інформаційної безпеки СБУ. Не плутати з Головне управління контррозвідувального захисту інтересів держави у сфе�...

Market town and civil parish in Lincolnshire, England This article is about the town in Lincolnshire. For other uses, see Sleaford (disambiguation). Town and civil parish in EnglandSleafordTown and civil parishClockwise from top: Aerial of Sleaford Castle site, Handley Monument, St Deny's Church, view across rooftops of Sleaford and Sessions House (on the right)SleafordLocation within LincolnshirePopulation19,807 (2021 Census)[1]OS grid referenceTF064455• London1...

Cet article traite de l'équipe masculine de basket-ball à trois. Pour l'équipe féminine de basket-ball à trois, voir Équipe de France féminine de basket-ball à trois. Équipe de France Généralités Zone FIBA FIBA Europe Couleurs Bleu, blanc, rouge Surnom Les Bleus Classement FIBA 4e (juillet 2024)[1] Palmarès Jeux olympiques Participations : 1 2024 Coupe du monde Phases finales : 5 2012 Coupe d'Europe Phases finales : 6 2019 Maillots Domicile &#...

Greek-French philosopher (1922–1997) Cornelius CastoriadisBorn(1922-03-11)11 March 1922Constantinople, Ottoman Empire (present-day Istanbul, Turkey)Died26 December 1997(1997-12-26) (aged 75)Paris, FranceNationalityGreek, French[78]Other namesCorneille Castoriadis,[79] Pierre Chaulieu, Paul Cardan, Jean-Marc CoudrayEducation8th Gymnasium of Athens[80]University of Athens(1937–1942: B.A., 1942)[81]University of Paris(Dr. cand., 1946–1948)[82&#...
この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典が不足しています。存命人物の記事は特に、検証可能性を満たしている必要があります。(2018年10月) 大言壮語的な記述になっています。(2018年10月) あまり重要でない事項が過剰に含まれているおそれがあり、整理が求められています。(2013年6月)出典検索?: 崎谷健次�...

RNF11 معرفات أسماء بديلة RNF11, SID1669, CGI-123, ring finger protein 11 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 612598 MGI: MGI:1352759 HomoloGene: 32195 GeneCards: 26994 علم الوجود الجيني وظائف جزيئية • ربط دي إن إي• GO:0001948، GO:0016582 ربط بروتيني• ربط أيون فلزي• GO:0050372 ubiquitin-protein transferase activity• GO:1904264، GO:1904...

Augustus ForsbergColonel Forsberg as wounded in Lynchburg, Virginia.Birth nameLudwig August ForsbergBorn(1832-01-13)January 13, 1832Stockholm, SwedenDiedJuly 15, 1910(1910-07-15) (aged 78)Lynchburg, VirginiaAllegiance Sweden Confederate States of AmericaService/branchRoyal Swedish Engineers Confederate States ArmyYears of serviceCa 1850-1855 (Sweden)1861–1865 (CSA)Rank Colonel, CSACommands 51st Virginia InfantryForsberg's BrigadeBattles/warsAmerican Civil War Battle...

Part of a series on thePolitics of Israel Basic Laws Jerusalem Law Law of Return Presidency President (list) Isaac Herzog Executive Prime Minister (list) Benjamin Netanyahu Alternate Prime Minister Office of the Prime Minister Deputy leaders Cabinet Current (37th) Security Cabinet Kitchen Cabinet Attorney General Gali Baharav-Miara Legislature Knesset Speaker: Amir Ohana Members (Arab) Leader of the Opposition Yair Lapid Knesset Guard State Comptroller Elections Political parties Elections La...
