תוחלת
|
Read other articles:

Lega Pro Prima Divisione 2011-2012 Competizione Lega Pro Prima Divisione Sport Calcio Edizione 34ª Organizzatore Lega Italiana Calcio Professionistico Date dal 4 settembre 2011al 10 giugno 2012 Luogo Italia Partecipanti 36 Formula 2 gironi all'italiana A/R, play-off e play-out Risultati Vincitore Ternana (1º titolo)Spezia (2º titolo) Altre promozioni Pro VercelliVirtus Lanciano Retrocessioni MonzaFolignoSPALPiacenzaBassanoTriestina Statistiche Miglior marcatore Gir. A: Ciro G...

American baseball player (1919–1972) For other people named Jackie Robinson, see Jackie Robinson (disambiguation). Baseball player Jackie RobinsonRobinson with the Brooklyn Dodgers in 1954Second basemanBorn: (1919-01-31)January 31, 1919Cairo, Georgia, U.S.Died: October 24, 1972(1972-10-24) (aged 53)Stamford, Connecticut, U.S.Batted: RightThrew: RightProfessional debutNgL: 1945, for the Kansas City MonarchsMLB: April 15, 1947, for the Brooklyn DodgersLast MLB ap...
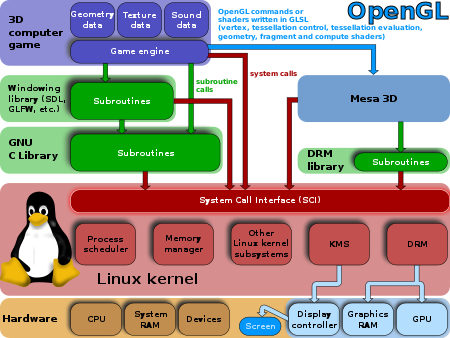
Diagramme montrant les nombreux composants systèmes avec lesquels un moteur de jeu est amené à interfacer sur Linux. Un moteur de jeu est un ensemble de composants logiciels qui effectuent des calculs de géométrie et de physique utilisés dans les jeux vidéo. L'ensemble forme un simulateur en temps réel souple qui reproduit les caractéristiques des mondes imaginaires dans lesquels se déroulent les jeux. Le but visé par un moteur de jeu est de permettre à une équipe de développeme...

Pour les articles homonymes, voir Institut national du patrimoine et INP. Institut national du patrimoineHistoireFondation 16 mai 1990Prédécesseur École du patrimoine (d)CadreType Établissements d'enseignement supérieur (Établissement public à caractère administratif)Forme juridique Autre établissement public national d'enseignementDomaine d'activité Enseignement supérieurSiège ParisPays FranceCoordonnées 48° 51′ 24″ N, 2° 21′ 08″ EL...

Pour les articles homonymes, voir Pompe (homonymie). Échange de CO2 entre l'air et la mer. Dans la biogéochimie des océans, la pompe biologique, qui relève du cycle du carbone océanique, est une série de processus biologiques conduisant à transporter le carbone de la zone photique vers les fonds marins. C'est un élément majeur du cycle du carbone. Grâce à cette pompe, l'océan a ainsi depuis le début de l'ère industrielle pu absorber 41 % du carbone anthropique émis par la...

Khan AcademyURLwww.khanacademy.orgTiperepositori video edukasiPerdagangan ?TidakRegistration (en)diperlukan untuk beberapa layananLanguebahasa Inggris AmerikaLisensiCreative Commons (BY-NC-SA)Bahasa pemrogramanJava PemilikSal KhanPembuatSal Khan, pendiri dan direktur eksekutifService entry (en)September 2006Lokasi kantor pusatMountain View NegaraAmerika Serikat Total omsetN/APeringkat Alexa 3,895 (June 2012[update])[1] Khan Academy adalah organisasi pendidikan non-profit ...

Внешняя политика Канады — это общий курс Канады в международных делах. Внешняя политика регулирует отношения Канады с другими государствами. Реализацией этой политики занимается Министерство иностранных дел Канады. История В 1909 году Канада открыла Департамент инос...

Questa voce o sezione sull'argomento centri abitati della Lombardia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Chignolo d'Isolacomune Chignolo d'Isola – VedutaVeduta LocalizzazioneStato Italia Regione Lombardia Provincia Bergamo AmministrazioneSindacoRamon Crespolini (Lega Salvini ...

Pour les articles homonymes, voir Benoist et Méchin. Jacques Benoist-MéchinJacques Benoist-Méchin en 1978.Titre de noblesseBaronBiographieNaissance 1er juillet 190117e arrondissement de ParisDécès 24 février 1983 (à 81 ans)18e arrondissement de ParisSépulture Cimetière du Père-Lachaise, tombeau de Benoist-Méchin (d)Nom de naissance Jacques Michel Gabriel Paul Benoist-MéchinNationalité françaiseFormation Université de ParisActivités Homme politique, historien, musicologue...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Kizzmekia CorbettLahirKizzmekia Shanta Corbett26 Januari 1986 (umur 38)Hurdle Mills, Carolina Utara, Amerika SerikatKebangsaanAmerika SerikatAlmamaterUniversity of Maryland, Baltimore CountyUniversity of North Carolina at Chapel HillPekerjaanImun...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2023) آلية الحماية المدنية في الاتحاد الأَوْرُبِّي (بالإنجليزية: Union Civil Protection Mechanism) يشير إلى اتفاقيات الاتحاد الأوربي التي تنظم زيادة التعاون بين أعضاء الاتحا�...

У этого термина существуют и другие значения, см. Следственный комитет. Следственный комитет при прокуратуре Российской Федерации Страна Россия Создана 7 сентября 2007 года Распущена (преобразована) 15 января 2011 года Юрисдикция Прокуратура Российской Федерации Предшес...

Battle of the Second English Civil War For the battle of the Jacobite rising of 1715, see Battle of Preston (1715). Battle of PrestonPart of the Second English Civil WarBattle of Preston 1648Date17–19 August 1648LocationPreston, LancashireResult Parliamentarian victoryBelligerents Royalists Scotland ParliamentariansCommanders and leaders Duke of Hamilton Earl of Callendar Earl of Middleton William Baillie Marmaduke Langdale Oliver Cromwell John LambertStrength 11,000 (Not all were engaged i...

Рондель ВПС України Список українських льотчиків, які загинули та постраждали під час російсько-української війни з 20 лютого 2014 року дотепер. В період з часу оголошення АТО та ООС під час бойових дій офіційно не повідомлялось про загибель пілотів, проте було декілька ава...

American professional wrestler (1934–2020) Mr. Wrestling IIMr. Wrestling II, c. 1977Birth nameJohn Francis Walker[1][2]Born(1934-09-10)September 10, 1934[3]Charleston, South Carolina, U.S.[3]DiedJune 10, 2020(2020-06-10) (aged 85)Honolulu, Hawaii, U.S.[2]Professional wrestling careerRing name(s)The Grappler[1]Johnny WalkerMr. WrestlingMr. Wrestling II[1]Billed height6 ft 0 in (1.83 m)[4]Billed weight24...

ستيفن أبياه معلومات شخصية الاسم الكامل ستيفن أبياه الميلاد 24 ديسمبر 1980 (العمر 43 سنة)أكرا الطول 1.78 م (5 قدم 10 بوصة) مركز اللعب وسط الجنسية غانا معلومات النادي النادي الحالي الزمالك المسيرة الاحترافية1 سنوات فريق مشاركات (أهداف) 1995–1997 هارتس أوف أوك 21 (19) 1997–2000 أودين...

Vincenzo Fiorillo Informasi pribadiTanggal lahir 13 Januari 1990 (umur 34)Tempat lahir Genoa, ItaliaTinggi 1,91 m (6 ft 3 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Pescara (pinjaman dari Juventus)Nomor 1Karier junior2004–2009 SampdoriaKarier senior*Tahun Tim Tampil (Gol)2008–2014 Sampdoria 4 (0)2010 →Reggina (pinjaman) 5 (0)2011 →Spezia (pinjaman) 8 (0)2012–2013 →Livorno (pinjaman) 28 (0)2014– Juventus 0 (0)2014– →Pescara (pinjaman) 0 (...

University of Malaya Kuala Lumpur gate L’University of Malaya (UM) è un'università pubblica in Malesia, la più antica del Paese. Si compone di 12 facoltà, 2 accademie e 3 poli accademici. Ha sede a Kuala Lumpur, capitale del Paese, tuttavia alcune strutture si trovano a Singapore. Studenti illustri Syed Amin Aljeffri Amani Williams Hunt Abdullah Sudirman Arshad Azalina Othman Said Abdul Khalid Ibrahim Mohamed Khaled Nordin Anwar Ibrahim Abdullah Ahmad Badawi Mahathir Mohamad Musa Hitam ...

Railway station in Rhondda Cynon Taf, Wales LlanharanLlanharan railway station from footbridgeGeneral informationLocationLlanharan, Rhondda Cynon TafWalesCoordinates51°32′17″N 3°26′28″W / 51.538°N 3.441°W / 51.538; -3.441Grid referenceST001830Managed byTransport for Wales RailPlatforms2Other informationStation codeLLRClassificationDfT category F2HistoryOriginal companySouth Wales RailwayPre-groupingGreat Western RailwayKey dates1850Opened2 November 1964Clos...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Politics of Macau – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this message) Politics and government of Macau Laws Basic Law National security law One country, two systems Sino–British Joint Declaration Capital punis...


![{\displaystyle \operatorname {E} X,\ \operatorname {E} (X),\ \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a833972e7b9628c337dfa2c28bb45eb2df9c22a)

































