ОфОћОюОЎОџ ОњОеОЮ-ОЕОъОЎОЊОў
|
Read other articles:

Gruppo di chimici al lavoro nei laboratori della Universidad de La Rioja in Spagna. Uno scienziato ├е una persona esperta in un determinato campo della scienza e che usa abitualmente metodi scientifici nell'effettuare ricerche scientifiche (i cui risultati vengono tipicamente pubblicati su apposite riviste scientifiche dopo attenta validazione da parte di specialisti del settore[1]), destinate all'incremento della conoscenza scientifica nello specifico settore di competenza. Indice 1 ...

Two are Company, Three Are None (1872), sebuah ukiran kayu oleh Winslow Homer. Kecemburuan seksual (Inggris: sexual jealousycode: en is deprecated ) adalah bentuk kecemburuan khusus dalam hubungan seksual, kecemburuan ini muncul akibat perselingkuhan seksual yang dicurigai, atau perselingkuhan yang sudah terjadi. Konsep ini dipelajari dalam bidang psikologi evolusioner. Para ahli psikologi evolusioner telah menjelaskan mengenai adanya perbedaan gender dalam kecemburuan seksual, perbedaan ini ...

Demonstrasi air mancur amonia Air mancur amonia adalah sebuah jenis demonstrasi kimia. Eksperimen tersebut dilakukan dengan memasukkan air ke dalam kontainer berisi gas amonia.[1] Amonia larut dalam air dan terjadi tekanan dalam kontainer tersebut. Akibatnya, air menjadi terangkat dan menciptakan efek air mancur. Demonstrasi tersebut memperkenalkan konsep seperti kelarutan dan hukum gas pada tingkat awal. Referensi ^ The Ammonia Smoke Fountain: An Interesting Thermodynamic Adventure M...

French sporting club Football clubMuretFull nameAmicale Sportive Muretaine footballFounded1903GroundStade Cl├Еment AderCapacity1,800ChairmanMarco Cafi├ЕroManagerChristophe TaineLeagueR├Еgional 1 Occitanie2021РђЊ22National 3 Group H: Occitanie, 13th (relegated)WebsiteClub website Amicale Sportive Muretaine is a club located in Muret, France. Founded in 1903, it is mostly known for its football teams. The women's team played in the highest level of league competition, Division 1 F├Еminine for t...

1969 Italian filmCerto certissimo... anzi probabileDirected byMarcello FondatoWritten byDacia MarainiStarringClaudia CardinaleCinematographyAlfio ContiniMusic byCarlo RustichelliRelease date 1969 (1969) Running time120 minutesCountryItalyLanguageItalian Certo certissimo... anzi probabile (Certain, Very Certain, As a Matter of Fact... Probable; English title Diary of a Telephone Operator[1]) is a 1969 Italian film based on the story of the same title by Dacia Maraini. It stars Cla...

Seorang biarawan Buddha di Sri Lanka. Biarawan adalah seorang laki-laki yang melakukan asketisme, memfokuskan pikiran dan raganya untuk agama. Konsep ini telah sangat lama ada dan dapat ditemukan pada berbagai agama seperti Kristen, Buddha, dll. Istilah ekivalen untuk perempuan adalah biarawati. Biarawan dalam agama Katolik adalah laki-laki yang menjadi anggota suatu ordo atau tarekat religus seperti Yesuit, Dominikan, Fransiskan, Benediktin dan sebagainya. Di Indonesia para biarawan kadang-k...

Dominican-American baseball pitcher (born 1988) In this Spanish name, the first or paternal surname is Chapman and the second or maternal family name is de la Cruz. Baseball player Aroldis ChapmanChapman with the New York Yankees in 2016Pittsburgh Pirates РђЊ No. 45PitcherBorn: (1988-02-28) February 28, 1988 (age 36)Holgu├Гn, CubaBats: LeftThrows: LeftMLB debutAugust 31, 2010, for the Cincinnati RedsMLB statistics (through April 15, 2024)WinРђЊloss record50РђЊ41Ear...

History of Communism in Peru This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Communism in Peru РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (April 2016) (Learn how and when to remove this message)Part of a series onCommunism Concepts Anti-capitalism Class conflict Class consciousness Classless society Collective leadership Communist party Communist rev...

Peter Graves (2009) Peter Graves (lahir 18 Maret 1926 - meninggal 14 Maret 2010) merupakan seorang aktor berkebangsaan Amerika Serikat yang menjadi terkenal saat bermain di film utamanya seperti Mission: Impossible dari 1967 hingga 1973. Dia dilahirkan di Minneapolis. Dia berkarier di dunia film sejak tahun 1942. Filmografi Winning Your Wings (1942) (short subject) Up Front (1951) Fort Defiance (1951) The Congregation (1952) Red Planet Mars (1952) Stalag 17 (1953) War Paint (1953) East of Sum...

Barangay in Makati City, Metro Manila, Philippines Barangay in National Capital Region, PhilippinesForbes ParkBarangayGate along EDSA Map of Makati with Forbes Park highlightedCountryPhilippinesRegionNational Capital RegionCityMakatiDistrictPart of the 1st district of MakatiFounded1940sNamed forWilliam Cameron ForbesGovernment Рђб TypeBarangay Рђб Barangay CaptainEvangeline Manotok Рђб Barangay Councilors Members Ana Maria BorromeoMaria Micaela RemullaMarcus Lesl...

Hospital in New York, United StatesRockland Psychiatric CenterNew York State Office of Mental HealthThe current main buildings at the Rockland Psychiatric Center in 2015GeographyLocationOrangeburg, New York, United StatesCoordinates41┬░02Рђ▓57.72Рђ│N 73┬░58Рђ▓07.7Рђ│W / 41.0493667┬░N 73.968806┬░W / 41.0493667; -73.968806OrganizationTypeSpecialistAffiliated universityNathan Kline Institute for Psychiatric ResearchServicesSpecialityPsychiatric hospitalHistoryFormer name(...

пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёп║пД┘Ёпе┘іпЕ пД┘ё┘Ѓ┘ѕпе┘іпЕ п║пД┘Ёпе┘іпД ┘Ѓ┘ѕпепД п║пД┘Ёпе┘іпД ┘Ѓ┘ѕпепД пфп╣п»┘і┘ё ┘Ёпхп»п▒┘і - пфп╣п»┘і┘ё пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёп║пД┘Ёпе┘іпЕ пД┘ё┘Ѓ┘ѕпе┘іпЕ ┘Є┘і пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёпФ┘єпДпд┘іпЕ пД┘ёпф┘і пфпг┘Ёп╣ пе┘і┘є п║пД┘Ёпе┘іпД ┘ѕ┘Ѓ┘ѕпепД.[1][2][3][4][5] ┘Ё┘ѓпДп▒┘єпЕ пе┘і┘є пД┘ёпе┘ёп»┘і┘є ┘Єп░┘Є ┘Ё┘ѓпДп▒┘єпЕ п╣пД┘ЁпЕ ┘ѕ┘Ёп▒пгп╣┘іпЕ ┘ё┘ёп»┘ѕ┘ёпф┘і┘є: ┘ѕпг┘Є пД┘ё┘Ё┘ѓпДп▒┘єпЕ п║пД┘Ёпе┘іпД ┘Ѓ┘ѕпепД №┐й...

лДл░ЛЂЛѓлИлйл░ ЛЂлхЛђЛќЛЌ л┐ЛђлЙлцЛќл╗лЙЛЂлЙЛёЛќЛЈLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesлЪл╗л░ЛѓлЙлйлџл░лйЛѓлЮЛќЛєЛѕлхлЉЛЃл┤л┤л░лџлЙлйЛёЛЃЛєЛќл╣лљл▓лхЛђЛђлЙлхЛЂ лцЛќл╗лЙЛЂлЙЛёлИ лЋл┐ЛќЛЂЛѓлхл╝лЙл╗лЙл│лИ лЋЛЂЛѓлхЛѓлИл║лИ лЋЛѓлИл║лИ лЏлЙл│Лќл║лИ люлхЛѓл░ЛёЛќлилИл║лИ лАлЙЛєЛќл░л╗ЛїлйлЙ-л┐лЙл╗ЛќЛѓлИЛЄлйЛќ ЛёЛќл╗лЙЛЂлЙЛёлИ лбЛђл░л┤лИЛєЛќЛЌ лљлйл░л╗ЛќЛѓлИЛЄлйл░ лљЛђЛќЛЂЛѓлЙЛѓлхл╗Лќл▓ЛЂЛїл║л░ лљЛёЛђлИл║л░лйЛЂЛїл║л░ лЉл╗лИлиЛїл║лЙЛЂЛЁЛќл┤лйл░ ЛќЛђл░лйЛЂЛїл║л░ лЉЛЃл┤л┤Лќл╣№┐й...

Argentine boxer Santos LaciarBornSantos Benigno Lacar (1959-01-31) January 31, 1959 (age 65)Huinca Renanc├│, C├│rdoba, ArgentinaNationalityArgentineOther namesFaluchoStatisticsWeight(s) Flyweight Super flyweight Height5 ft 1 in (155 cm)Reach62+1⁄2 in (159 cm)StanceOrthodox Boxing recordTotal fights101Wins79Wins by KO31Losses10Draws11 Santos Benigno Laciar (born January 31, 1959), known familiarly as Santos Laciar and nicknamed Falucho, is an Argentine ...
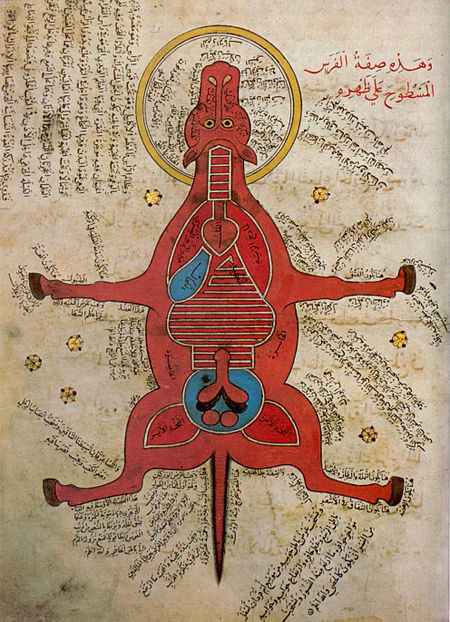
пгп▓пА ┘Ё┘є п│┘ёп│┘ёпЕ ┘Ё┘ѓпД┘ёпДпф пГ┘ѕ┘ёпД┘ёпЦп│┘ёпД┘Ё пД┘ёп╣┘ѓ┘іп»пЕ пД┘ёпЦ┘і┘ЁпД┘є пф┘ѕпГ┘іп» пД┘ё┘ё┘Є пД┘ёпЦ┘і┘ЁпД┘є пепД┘ё┘Ё┘ёпДпд┘ЃпЕ пД┘ёпЦ┘і┘ЁпД┘є пепД┘ё┘Ѓпфпе пД┘ёп│┘ЁпД┘ѕ┘іпЕ пД┘ёпЦ┘і┘ЁпД┘є пепД┘ёп▒п│┘ё ┘ѕпД┘ёпБ┘єпе┘іпДпА пД┘ёпЦ┘і┘ЁпД┘є пепД┘ё┘і┘ѕ┘Ё пД┘ёпбп«п▒ пД┘ёпЦ┘і┘ЁпД┘є пепД┘ё┘ѓпХпДпА ┘ѕпД┘ё┘ѓп»п▒ пБп▒┘ЃпД┘є пД┘ёпЦп│┘ёпД┘Ё п┤┘ЄпДп»пЕ пБ┘є ┘ёпД пЦ┘ё┘Є пЦ┘ёпД пД┘ё┘ё┘Є ┘ѕпБ┘є ┘ЁпГ┘Ёп» п▒п│┘ѕ┘ё пД┘ё┘ё┘Є пЦ┘ѓпД┘ЁпЕ пД┘ёпх┘ёпДпЕ пЦ┘іпфпДпА пД┘ёп▓┘ЃпДпЕ пх┘ѕ┘Ё п▒┘Ё№┐й...

2007 WD5Discovery[1]Discovered byMount Lemmon SurveyAndrea Boattini(unofficial credits)Discovery date20 November 2007DesignationsMinor planet categoryNEO · Apollo[1][2]Mars-crosserOrbital characteristics[2]Epoch 13 January 2016 (JD 2457400.5)Uncertainty parameter 5[2] · 0[1]Aphelion3.9289 AU (587.76 Gm)Perihelion0.991120 AU (148.2694 Gm)Semi-major axis2.4600 AU (368.01 Gm)...

┘ЁпД┘ё┘ѕ┘ЁпД (пепД┘ёпЦп│пепД┘є┘іпЕ: Juan Luis Londo├▒o Arias)РђЈ[1] ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пДп│┘Ё пД┘ё┘ѕ┘ёпДп»пЕ (пепД┘ёпЦп│пепД┘є┘іпЕ: Juan Luis Londo├▒o Arias)РђЈ[1] пД┘ё┘Ё┘і┘ёпДп» 28 ┘і┘єпД┘іп▒ 1994 (30 п│┘єпЕ)[2][3] ┘Ё┘іп»┘і┘ё┘і┘є[4] ┘Ё┘ѕпДпи┘єпЕ ┘Ѓ┘ѕ┘ё┘ѕ┘Ёпе┘іпД пД┘ёпГ┘іпДпЕ пД┘ё┘Ђ┘є┘іпЕ пД┘ё┘є┘ѕп╣ пе┘ѕпе п▒┘ѕ┘Ѓ[5]пї ┘ѕп▒┘іп║┘і┘Є пф┘ѕ┘є[5]пї ┘ѕпД┘ёпфп▒пДпе пД┘ё┘ёпДпф┘і┘є┘і №┐й...

Martin Luther King Jr. PlazaToledo, OHGeneral informationLocation415 Emerald AvenueToledo, OhioUnited StatesCoordinates41┬░38Рђ▓16Рђ│N 83┬░32Рђ▓30Рђ│W / 41.63778┬░N 83.54167┬░W / 41.63778; -83.54167Owned byToledoРђЊLucas County Port AuthorityPlatforms3 island platforms (formerly 6 island platforms)Tracks2 (formerly 12)Connections Amtrak Thruway Barons Bus Lines Greyhound LinesConstructionParkingYesAccessibleYesOther informationStation codeAmtrak: TOLHistoryOpened1950Re...

Planned science mission to Mars featuring semi-hard landing strategy This article is about the atmospheric science mission to Mars. For the MnSCU network website, see Metnet (website). Mars MetNetMars MetNet impactor conceptMission typeTechnologyAtmospheric scienceOperatorFinnish Meteorological InstituteWebsitehttp://fmispace.fmi.fi/index.php?id=metnet Spacecraft propertiesLanding massentry mass: 22.2 kg per unit[1]Payload mass4 kg allocationDimensionsImpactor: 1.8 m diameter[2 ...

French count; legitimized son of Louis XIV (1667РђЊ1683)This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Louis, Count of Vermandois РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (July 2024) (Learn how and when to remove this message) LouisCount of VermandoisBornLouis de La Blaume Le Blanc(1667-10-02)2 October...


























![{\displaystyle \mathbb {R} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)











