ОЕОцОћ ОъОАОЊОе ОеОљОЕОЋОЪ
|
Read other articles:

Artikel ini bukan mengenai Desikasi. Bagian medulla oblongata di tingkat dekusasi piramida. Dekusasi dipakai dalam konteks biologi untuk mendeskripsikan persilangan (Latin: penomoran Romawi untuk angka sepuluh, deca, ditulis 'X'). Dalam istilah anatomi Latin, bentuk decussatio dipakai, contoh decussatio pyramidum. Selain itu, istilah anatomi chiasma mengambil nama dari huruf Yunani '╬Д', chi, Sedangkan deskusasi mengacu pada persimpangan di dalam sistem saraf pusat , berbagai jenis penyeberan...

The Arc de Triomphe of Place de l'├Ѕtoile: salah satu bangunan di Prancis yang menggunakan gaya empire Gaya Imperium adalah gaya dalam arsitektur bangunan, rumah atau perabotan rumah yang berkembang di Eropa.[1] Gaya ini merupakan fase utama seni neo-klasik yang berkembang di Prancis pada masa kekaisaran pertama (1804-1814).[2] Gaya imperium berasal dari gaya Louis XVI yang klasik dan mewah serta dipengaruhi oleh bentuk-bentuk gaya Yunani, Romawi dan Mesir.[2] Ciri-cir...

Indonesia padaPesta Olahraga AsiaKode IOCINAKONKomite Olimpiade IndonesiaMedaliPeringkat ke-11 98 130 264 Total 492 Penampilan pada Pesta Olahraga Asia (ringkasan)195119541958196219661970197419781982198619901994199820022006201020142018Penampilan Musim Dingin2017 Indonesia pertama kali ikut serta dalam Asian Games pada tahun 1951 dan tak pernah absen pada tahun-tahun berikutnya. Pada tahun 1962, Indonesia menjadi tuan rumah Asian Games. Kemudian, pada tahun 2018, Indonesia kembali menjadi tuan...

Chrysostomos dari Smirna. Krisostomus Kalafatis (Yunani: ¤Є¤Ђ¤Ё¤Ѓ¤ї¤Ѓ¤ё╬┐╬╝╬┐¤ѓ ╬║╬▒╬╗╬▒¤є╬г¤ё╬и¤ѓ ; 1867 - 1922) Krisostomus dari Smirna, Krisostomos dari Smirna dan Metropolitan Krisostomus, adalah uskup metropolitan Ortodoks Yunani. Ia lahir di Treglia (sekarang zeytinba─Ъ─▒), Turki pada tahun 1867. Ia membantu kampanye Yunani di Smirna pada tahun 1919 dan kemudian dibunuh oleh massa setelah kota itu akhirnya diduduki oleh pasukan Turki dalam Perang Yunani-Turki tahun 1919-1922. Sinod...

Pub in Kensington High Street, London, England The Goat, KensingtonThe Goat Tavern, Kensington, LondonThe GoatShow map of Royal Borough of Kensington and ChelseaThe GoatShow map of Greater LondonGeneral informationAddress3a Kensington High StreetTown or cityLondonCountryEnglandCoordinates51┬░30Рђ▓08Рђ│N 0┬░11Рђ▓16Рђ│W / 51.5022┬░N 0.1877┬░W / 51.5022; -0.1877Construction started1695 The Goat is a public house in Kensington, London, at 3a Kensington High Street, which d...

2010 South Korean filmNo MercyTheatrical posterDirected byKim Hyeong-junWritten byKim Hyeong-junProduced byKang Woo-sukStarringSol Kyung-gu Ryoo Seung-bumCinematographyKim Woo-hyungEdited byKim Sun-minMusic byPark Ji-manProductioncompaniesCinema Service The Dream&PicturesDistributed byCJ Entertainment[1][2]Release date January 7, 2010 (2010-01-07) Running time125 minutesCountrySouth KoreaLanguageKoreanBox officeUS$7.58 million No Mercy (Korean: ВџЕ№┐й...
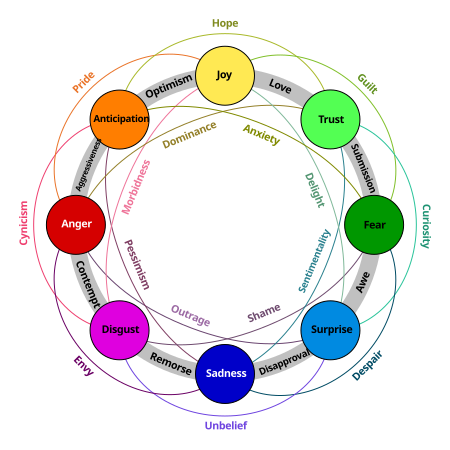
Thoughts, images, emotions, and actions of a pessimistic nature Worriers redirects here. For the band, see Worriers (band). For other uses, see Worry (disambiguation). Part of a series onEmotions Affect Classification In animals Emotional intelligence Mood Regulation Interpersonal Dysregulation Valence Emotions Acceptance Admiration Affection Amusement Anger Angst Anguish Annoyance Anticipation Anxiety Apathy Arousal Awe Belongingness Boredom Confidence Confusion Contempt Contentment Courage ...

сЃесЃЈсЃЇсѓ╣12СИќ угг130С╗Б сЃГсЃ╝сЃъТЋЎуџЄ ТЋЎуџЄт░▒С╗╗ 955т╣┤12Тюѕ16ТЌЦТЋЎуџЄжЏбС╗╗ 964т╣┤5Тюѕ14ТЌЦтЁѕС╗Б сѓбсѓгсЃџсЃѕсѓЦсѓ╣2СИќТгАС╗Б сЃгсѓф8СИќтђІС║║ТЃЁта▒тЄ║ућЪ 937т╣┤сѓ╣сЃЮсЃгсЃ╝сЃѕтЁгтЏй№╝ѕСИГжЃесѓцсѓ┐сЃфсѓб№╝Ѕсѓ╣сЃЮсЃгсЃ╝сЃѕТГ╗тј╗ 964т╣┤5Тюѕ14ТЌЦ ТЋЎуџЄжаўсђЂсЃГсЃ╝сЃътјЪтЏйу▒Ї сѓ╣сЃЮсЃгсЃ╝сЃѕтЁгтЏйУдф уѕХсѓбсЃФсЃЎсЃфсЃ╝сѓ│2СИќ№╝ѕсѓ╣сЃЮсЃгсЃ╝сЃѕтЁг№╝ЅсђЂТ»ЇсѓбсЃФсЃђсЂЮсЂ«С╗ќсЂ«сЃесЃЈсЃЇсѓ╣сЃєсЃ│сЃЌсЃгсЃ╝сЃѕсѓњУАеуц║ сЃесЃЈсЃЇсѓ╣12СИќ№╝ѕIoannes XIIсђЂ937т╣┤ - 964т╣┤5Тюѕ14ТЌЦ№╝ЅсЂ»сђЂсЃГ...

п│┘ѕ┘є┘і┘Ѓ п»п▒┘і┘Ёп▓ ┘Ѓ┘ѕ┘ё┘Ѓп┤┘є Sonic Dreams Collection пД┘ё┘Ёпи┘ѕп▒ пбп▒┘ЃпД┘і┘є ┘Ѓ┘іп»п▓ пД┘ё┘єпДп┤п▒ пбп▒┘ЃпД┘і┘є ┘Ѓ┘іп»п▓ п│┘ёп│┘ёпЕ пД┘ё┘ёп╣пепЕ пД┘ё┘ѓ┘є┘Ђп░ п│┘ѕ┘є┘і┘Ѓ (п║┘іп▒ п▒п│┘Ё┘іпД┘І) ┘ЁпГп▒┘Ѓ пД┘ё┘ёп╣пепЕ ┘і┘ѕ┘є┘іпф┘і пД┘ё┘єпИпД┘Ё ┘ЁпД┘і┘Ѓп▒┘ѕп│┘ѕ┘Ђпф ┘ѕ┘і┘єп»┘ѕп▓пї ┘ЁпД┘Ѓ пБ┘ѕ пЦп│ пфпДп▒█їп« пД┘ёпЦпхп»пДп▒ 10 пБп║п│пип│ 2015 ┘є┘ѕп╣ пД┘ё┘ёп╣пепЕ ┘ЁпГпД┘ЃпДпЕ п│пДп«п▒пЕ пД┘ё┘є┘Ёпи ┘ёп╣пепЕ ┘Ђ┘іп»┘і┘ѕ ┘Ђп▒п»┘іпЕ пД┘ё┘Ё┘ѕ┘ѓп╣ пД┘ёп▒п│┘Ё┘і пД┘ё┘Ё┘ѕ┘ѓп╣ пД┘ёп▒п│┘Ё┘і пфп╣п»№┐й...

У▒фТаёжЂЊ У▒фтцфжЃј та┤ТЅђтЁЦсѓісЂЎсѓІУ▒фТаёжЂЊтЪ║уцјТЃЁта▒тЏЏУѓАтљЇ ТЙцС║Ћ У▒фтцфжЃјРєњУ▒фТаёжЂЊ У▒фтцфжЃјТюгтљЇ ТЙцС║Ћ У▒фтцфжЃјТёЏуД░ сѓ┤сѓдсѓ┐сЃГсѓдсђЂУ▒фсЂАсѓЃсѓЊсђЂGAD[1][2]ућЪт╣┤ТюѕТЌЦ (1986-04-06) 1986т╣┤4Тюѕ6ТЌЦ№╝ѕ38ТГ│№╝ЅтЄ║У║Ф тцДжўфт║ют»Ют▒ІтиЮтИѓУ║ФжЋи 183cmСйЊжЄЇ 160kgBMI 47.26ТЅђт▒ъжЃет▒І тбЃтиЮжЃет▒ІтЙЌТёЈТіђ тЈ│тЏЏсЂцсЃ╗тЄ║сЂЌТіЋсЂњсЃ╗тѕЄсѓіУ┐ћсЂЌсЃ╗тцќТјЏсЂЉсЃ╗ждќТіЋсЂњсЃ╗тЈ│СИІТЅІТіЋсЂњТѕљуИЙуЈЙтюесЂ«уЋфС╗ў т╝ЋжђђТюђжФўСйЇ ТЮ▒тцДжќбућЪТХ»ТѕдТГ┤ 696тІЮ493ТЋЌ...

Disambiguazione РђЊ Se stai cercando altri significati, vedi Ventimiglia (disambigua). Ventimigliacomune Ventimiglia РђЊ VedutaLa citt├а vecchia di Ventimiglia LocalizzazioneStato Italia Regione Liguria Provincia Imperia AmministrazioneSindacoFlavio Di Muro (Lega) dal 29-5-2023 TerritorioCoordinate43┬░47Рђ▓25Рђ│N 7┬░36Рђ▓30Рђ│E / 43.790278┬░N 7.608333┬░E43.790278; 7.608333№╗┐ (Ventimiglia)Coordinate: 43┬░47Рђ▓25Рђ│N 7┬░36Рђ▓30Рђ│E / 43.790...

This is a list of members of the Victorian Legislative Assembly as elected at the 29 December 1908 election and subsequent by-elections up to the election of 16 November 1911.[1] Note the Term in Office refers to that members term(s) in the Assembly, not necessarily for that electorate. Name Party[2] Electorate Term in Office Frank Anstey [a] Labor Brunswick 1902РђЊ1910 Reginald Argyle Anti-Socialist Dalhousie 1900РђЊ1914 Samuel Barnes [c] VFU Walhalla 1910РђЊ1927 Norman Bayl...

пД┘ё┘ёп║пЕ пД┘ё┘Ёпгп▒┘іпЕ пД┘ёпДп│┘Ё пД┘ёп░пДпф┘і (пепД┘ё┘Ёпгп▒┘іпЕ: magyar nyelv)РђЈ(пепД┘ё┘Ёпгп▒┘іпЕ: magyar)РђЈ пД┘ё┘єпДпи┘ѓ┘ѕ┘є 12600000 (┘ёп║пЕ пБ┘Ё) (2019) пД┘ё┘ЃпфпДпепЕ пЦп«пипДпипЕ ┘ёпДпф┘і┘є┘іпЕ пД┘ё┘єп│пе ┘ёп║пДпф пБ┘ѕп▒пД┘ё┘іпЕ ┘ёп║пДпф пБ┘ѕп▒пД┘ё┘іпЕ┘ёп║пДпф пБ┘ѕп║п▒┘іпЕпД┘ё┘Ёпгп▒┘іпЕ пБ┘іп▓┘ѕ 639-1 hu пБ┘іп▓┘ѕ 639-2 hun пБ┘іп▓┘ѕ 639-3 hun пфп╣п»┘і┘ё ┘Ёпхп»п▒┘і - пфп╣п»┘і┘ё пД┘ё┘ёп║пЕ пД┘ё┘Ёпгп▒┘іпЕ (magyar nyelv) ┘Є┘і пД┘ё┘ёп║пЕ...

Private, boarding school in East Machias, Maine, United StatesWashington AcademyAddress66 Cutler RoadEast Machias, Maine 04630United StatesCoordinates44┬░44Рђ▓03Рђ│N 67┬░23Рђ▓19Рђ│W / 44.7343┬░N 67.3885┬░W / 44.7343; -67.3885InformationSchool typePrivate, boardingMottoVirtute de Regno Certam(The Virtue of the Kingdom is Certain)Founded1792; 232 years ago (1792)Head of schoolRichard OlivaresGrades9-12Enrollment392Student to teacher ratio10:1Campus type...

Chronologies Donn├Еes cl├Еs 1799 1800 1801 1802 1803 1804 1805D├Еcennies :1770 1780 1790 1800 1810 1820 1830Si├еcles :XVIIe XVIIIe XIXe XXe XXIeMill├Еnaires :-Ier Ier IIe IIIe Chronologies g├Еographiques Afrique Afrique du Sud, Alg├Еrie, Angola, B├Еnin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, R├Еpublique centrafricaine, Comores, R├Еpublique du Congo, R├Еpublique d├Еmocratique du Congo, C├┤te d'Ivoire, Djibouti, ├Ѕgyp...

Former congressional district Georgia's at-large congressional districtObsolete districtCreated179018291880Eliminated182018451885Years active1793РђЊ18271829РђЊ18451883РђЊ1885 From 1793 to 1827 and again from 1829 to 1845, Georgia elected all its Representatives in Congress from a single multi-member at-large congressional district: From 1793 to 1803, Georgia elected 2 Representatives at large. From 1803 to 1813 Georgia elected 4 Representatives at large. From 1813 to 1823 Georgia elected 6 Re...

American jazz musician and band leader (1904РђЊ1957) For the American sport shooter, see Jimmie Dorsey (sport shooter). Jimmy DorseyDorsey in 1943Background informationBirth nameJames Francis DorseyBorn(1904-02-29)February 29, 1904Shenandoah, Pennsylvania, U.S.DiedJune 12, 1957(1957-06-12) (aged 53)New York City, NY, U.S.GenresBig bandswingDixielandOccupation(s)BandleadermusiciancomposerInstrument(s)SaxophoneclarinettrumpetYears active1913РђЊ1957Musical artist James Francis Dorsey (Febru...

American singer Jimmy UrineUrine performing in December 2013Background informationBirth nameJames EuringerBorn (1969-09-07) September 7, 1969 (age 54)New York City, U.S.Genres Electropunk industrial rock electronic rock Occupation(s) Musician singer songwriter Instrument(s) Vocals programming Member of Mindless Self Indulgence The Left Rights Euringer Musical artist James Euringer (born September 7, 1969), better known as Jimmy Urine, is an American musician, singer, and songwriter. He i...

Political theory developed by Vladimir Lenin This article is about political theory developed originally by Lenin. For the political theory and state ideology developed by Stalin, see MarxismРђЊLeninism. For the political ideology and branch of Marxism developed by Trotsky, see Trotskyism. Vladimir Lenin, whose policies and politics allowed the Bolshevik vanguard party to realise the October Revolution in Russia in 1917 Part of a series onLeninism Schools of thought Bolshevism Bordigism Marxi...

Women's 800 metres at the 1999 World ChampionshipsVenueEstadio Ol├ГmpicoDates21 August (heats)22 August (semifinals)24 August (final)Competitors37 from 31 nationsWinning time1:56.68Medalists Ludmila Formanov├А Czech Republic (CZE) Maria de Lurdes Mutola Mozambique (MOZ) Svetlana Masterkova Russia (RUS)← 19972001 → Events at the1999 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwome...


































