שדה וקטורי משמר
|
Read other articles:

Perang Saudara RusiaBagian dari Setelah Perang Dunia I dan Revolusi RusiaSearah jarum jam di atas:Tentara Don pada 1919; divisi putih infanteri pada Maret 1920; tentara Tentara Kavaleri 1; Leon Trotsky pada 1918; penggantungan para pekerja di (Dnipro) oleh Tentara Austria-Hungaria, April 1918.Tanggal7 November 1917 – 25 Oktober 1922/16 Juni 1923[1][2](Pemberontakan Perlawanan terhadap Soviet berlanjut di Asia Tengah hingga 1934)LokasiBekas Kekaisaran Rusia, Galisia, Mongolia...

American politician Westman in 2020 Richard A. Westman (born 1959) is a Republican politician who was elected and currently serves in the Vermont House of Representatives.[1] He was a Representative of the Lamoille-4 Representative District. Since 2011, he has served as state senator for Lamoille district. References ^ List of Representatives in the Vermont House of Representatives from the state legislators database -- Adam Brown, BYU Political Science. vteMembers of the Vermont Sena...

Fictional group of comic book supervillains from DC Comics This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (October 2023) (Learn how and when to remove this template message) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (October 2023) Fearsome FiveThe Fearsome Five, from the co...
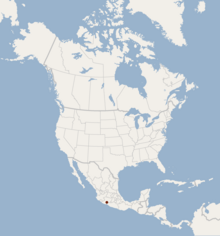
Species of bat found in Mexico Least yellow bat Conservation status Vulnerable (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Chiroptera Family: Vespertilionidae Genus: Rhogeessa Species: R. mira Binomial name Rhogeessa miraLaVal, 1973 The least yellow bat (Rhogeessa mira) is a species of vesper bat found only in Mexico. References ^ Arroyo-Cabrales, J.; Ospina-Garces, S. (2016). Rhogeessa mira. IUCN Red L...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

American college basketball season 2023–24 Western Illinois Leathernecks men's basketballConferenceOhio Valley ConferenceRecord21–12 (13–5 OVC)Head coachChad Boudreau (1st season)Associate head coachKyle HeikkinenAssistant coaches Chris Hill John Clancy Kamrein Street Kris Glover Home arenaWestern HallSeasons← 2022–232024–25 → 2023–24 Ohio Valley Conference men's basketball standings vte Conf Overall Team W L PCT W L ...

Untuk kegunaan lain, lihat Cempedak (disambiguasi). Cempedak Artocarpus integer TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladfabidsOrdoRosalesFamiliMoraceaeTribusArtocarpeaeGenusArtocarpusSpesiesArtocarpus integer Merr. Tata namaBasionimRadermachia integra lbs Cempedak adalah tanaman buah-buahan dari famili Moraceae. Bentuk buah, rasa, dan keharumannya seperti nangka, meski aromanya kerap kali me...

Irreligious and anti-clerical element of Marxism–Leninism Part of a series onMarxism–Leninism Concepts Administrative-command system Anti-imperialism Anti-revisionism Central planning Soviet-type economic planning Collective farming Collective leadership Commanding heights of the economy Democratic centralism Dialectical logic Dialectical materialism Foco Intensification of the class struggleunder socialism Labor aristocracy Marxist–Leninist atheism One-party state Partiinost' People's ...

Rexingencomune Rexingen – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementSaverne CantoneIngwiller TerritorioCoordinate48°54′N 7°11′E / 48.9°N 7.183333°E48.9; 7.183333 (Rexingen)Coordinate: 48°54′N 7°11′E / 48.9°N 7.183333°E48.9; 7.183333 (Rexingen) Superficie2,33 km² Abitanti196[1] (2009) Densità84,12 ab./km² Altre informazioniCod. postale67320 Fuso orarioUTC+1 Codice INS...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Lifestyle brand (founded 2011) Brit + CoCompany typePrivateIndustryInternet commerce and mediaFounded2011FounderBrit MorinHeadquartersSan FranciscoServicesMedia companyWebsitebrit.co Brit + Co is a website and lifestyle brand targeted at women. The company was founded by Brit Morin in 2011.[1] History Brit + Co was founded in late 2011 by Brit Morin, who served as CEO.[1] In January 2018, the company hired Jill Braff, a former general manager of Ellen Digital Ventures, as its ...

Village in LithuaniaMačiuliškėsVillageMačiuliškėsLocation of MačiuliškėsCoordinates: 54°42′14″N 25°41′35″E / 54.70389°N 25.69306°E / 54.70389; 25.69306Country LithuaniaCountyVilnius CountyMunicipalityVilnius District MunicipalityEldershipLavoriškės eldershipPopulation (2011) • Total10Time zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST) Mačiuliškės (Belarusian: Мацюлішкі, Polish: Maciuliszki) is a village i...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Andrew Z. Fire Andrew Z. Fire (lahir 1959) adalah penerima Hadiah Nobel dalam Fisiologi atau Kedokteran bersama Craig C. Mello untuk penjelasan mengenai interferensi RNA dan teknik pemanfaatannya. Penelitian ini dilakukan di Institusi Carnegie Washington dan dipublikasikan pada 1998. Fire kini menjabat sebagai profesor patologi dan genetika di Universitas Stanford. Biografi Fire dilahirkan di Palo Alto, California dan dibesarkan di Sunnyvale, California.[1] Setelah lulus dari Sekolah ...

Kakao Proses BelandaBubuk kakao Proses Belanda (kiri) dibandingkan dengan bubuk kakao alami (kanan)Nama lainKakao BelandaJenisKakaoTempat asalBelandaDibuat olehCoenraad Johannes van HoutenBahan utamaBubuk kakao dengan bahan alkaliSunting kotak info • L • BBantuan penggunaan templat ini Bubuk Kakao Proses Belanda atau Dutch Cocoa adalah kakao yang diproses dengan agen alkali agen untuk mengubah warnanya dan menghasilkan rasa yang lebih lembut dibandingkan kakao alami yang diekstr...

Electric multiple unit that operates Eurostar's high-speed rail service British Rail Class 373Eurostar e300TGV TMSTA refurbished Class 373 at Gare d'Albertville in 2018The standard-class interior of a refurbished Class 373In service14 November 1994 – presentManufacturerGEC AlsthomBrugeoise et NivellesBuilt atLa Rochelle, FranceBelfort, FranceWashwood Heath, EnglandBruges, BelgiumFamily nameTGVConstructed1992–1996Number built38(31 × Three Capitals, 7 × North of London)Number...

Voce principale: Associazione Sportiva Pro Gorizia. Associazione Sportiva Pro GoriziaStagione 1942-1943Sport calcio Squadra Pro Gorizia Allenatore Aldo Paolo Tacchini Presidente Aldo Paolo Tacchini Serie C1º posto nel girone A, 1º posto girone finale B. Promosso in Serie B. 1941-1942 1943-1944 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Sportiva Pro Gorizia nelle competizioni ufficiali della stagione 1942-1943. Indice 1 Stagi...

Recurrent layer of air pollution covering South Asia This article is about the Indian Ocean brown cloud. For China, see Air pollution in China. The Indian Ocean brown cloud or Asian brown cloud is a layer of air pollution that recurrently covers parts of South Asia, namely the northern Indian Ocean, India, and Pakistan.[1][2] Viewed from satellite photos, the cloud appears as a giant brown stain hanging in the air over much of the Indian subcontinent and the Indian Ocean every...

American congressionally chartered fraternal organization Sons of Union Veterans of the Civil WarAbbreviationSUVCWPredecessorGrand Army of the RepublicEstablishedOrganized November 12, 1881, chartered by Congress on August 20, 1954TypePatriotic-Hereditary societyLegal statusCongressionally chartered non-profit corporationPurposeHistorical, benevolentHeadquartersHarrisburg, PennsylvaniaMembership (2022) 6,574Commander-in-ChiefPeter J. HritskoSenior Vice Commander-in-ChiefKevin L. MartinJunior ...

French footballer (born 2002) Bradley Barcola Barcola with Lyon in 2023Personal informationFull name Bradley Laurent Barcola[1]Date of birth (2002-09-02) 2 September 2002 (age 21)Place of birth Villeurbanne, FranceHeight 1.82 m (6 ft 0 in)[2]Position(s) Forward, winger[2]Team informationCurrent team Paris Saint-GermainNumber 29Youth career2008–2010 AS Buers Villeurbanne2010–2021 LyonSenior career*Years Team Apps (Gls)2020–2023 Lyon II 22 (5)20...

























