ציר רדיקלי

בגאומטריה, ציר רדיקלי של שני מעגלים הוא המקום הגאומטרי של כל הנקודות שהחזקות שלהן ביחס לשני המעגלים שוות. זהו תמיד קו ישר. לציר הרדיקלי תפקיד חשוב בתאוריה של אינוורסיה במעגל.

לכל שני מעגלים שאינם בעלי מרכז משותף יש ציר רדיקלי. הציר הרדיקלי הוא תמיד קו ישר; אם המעגלים נחתכים, זהו הישר העובר דרך נקודות החיתוך.

משפחות קואקסליות

איור 1: נציגים של שתי משפחות קואקסליות משלימות. הישר החום הוא הציר הרדיקלי של המעגלים בירוק, והישר השחור הוא הציר הרדיקלי של המעגלים בכחול. הנקודות האדומות הן נקודות הגבול של המשפחה הירוקה

נניח שהישר t הוא הציר הרדיקלי של המעגלים C1 ו-C2. מעגל C ש-t הוא הציר הרדיקלי שלו ושל C1 נקרא מעגל קואקסלי ("בעל ציר משותף") עם C1 ו-C2; קבוצת כל המעגלים האלה (לרבות C1 ו-C2) נקראת המניפה הקואקסלית (pencil of coaxal circles) של C1 ו-C2. לכל שני מעגלים במשפחה הזו יש אותו ציר רדיקלי, והמרכזים שלהם נמצאים על ישר אחד, המאונך לציר. אינוורסיה במעגל מעבירה מניפה קואקסלית למניפה קואקסלית.

תהי P נקודה על הציר הרדיקלי של שני מעגלים; ל-P יש אותה חזקה ביחס לכל אחד מהמעגלים, ואם החזקה הזו חיובית (היינו P מחוץ לאחד המעגלים, ולכן מחוץ לכולם), אז מעגל שמרכזו P ורדיוסו הוא שורש החזקה חוצה במאונך את כל המעגלים במשפחה הקואקסלית. אפשר לבחור נקודה נוספת על הציר הרדיקלי, וליצור גם סביבה מעגל החוצה במאונך את כל המעגלים במניפה. המשפחה הקואקסלית של שני המעגלים האלה משלימה למשפחה המקורית: כל מעגל מאחת המשפחות חוצה במאונך כל מעגל מן המשפחה השנייה. אם המעגלים במניפה קואקסלית אינם חוצים זה את זה, אז המעגלים במניפה המשלימה עוברים כולם דרך אותן שתי נקודות, הנקראות נקודות הגבול של המשפחה הראשונה (ואכן, ככל שהמעגל קטן יותר, כך קרוב יותר מרכזו לאחת מנקודות הגבול). ראו איור 1.

בנייה בסרגל ובמחוגה

איור 2: בניית הציר הרדיקלי (בירוק) של שני מעגלים נתונים (בכחול): מעבירים מעגל המשיק במשותף לשני המעגלים (באדום, ראו כיצד באיור 3); הציר הרדיקלי הוא הישר (בירוק) היורד מחיתוך המשיקים (הנקודה הירוקה) במאונך לישר המחבר את מרכזי המעגלים
איור 3: בניית המעגלים (באדום) המשיקים במשותף לשני מעגלים נתונים (בכחול), דרך נקודה נתונה על אחד מהם (גם כן בכחול): מסמנים את נקודות הדמיון של שני המעגלים (בירוק), ומחברים אותן אל הנקודה; שתיים מארבע נקודות החיתוך של הישרים האלו עם המעגל השני, הן נקודות השקה של מעגל העונה על הדרישה

העובדה שאפשר לבנות את הציר הרדיקלי בסרגל ובמחוגה (ראו איורים 2 ו-3) מקנה לו תפקיד מועיל בבניות גאומטריות שונות.

מרכז החזקה של שלושה מעגלים

יהיו C1,C2,C3 שלושה מעגלים שאינם קואקסליים, ואינם קונצנטריים. הצירים הרדיקליים של כל שניים מן המעגלים האלה, נפגשים בנקודה אחת הנקראת מרכז החזקה של המעגלים. בעזרת מרכז החזקה, אפשר לבנות את שני המעגלים המשיקים במשותף ל-C1,C2,C3, באופן הבא:

  1. מצא את נקודות הדמיון של כל שני מעגלים.
  2. העבר ישר דרך שלוש נקודות הדמיון החיצוניות (ישר זה נקרא ישר ד'לאמבר של שלושת המעגלים).
  3. לכל i=1,2,3, הורד אנך מן המרכז של Ci אל ישר ד'לאמבר, ומצא על ידי אינוורסיה במעגל Ci את הנקודה הצמודה למפגש האנך עם הישר.
  4. הוצא ממרכז החזקה קרניים אל שלוש הנקודות שהתקבלו. הקרניים האלה פוגשות את שלושת המעגלים בפנים ובחוץ.
  5. המעגל החוסם את המשולש שקודקודיו הם נקודות המפגש הפנימיות, והמעגל החוסם את המשולש שקודקודיו הם נקודות המפגש החיצוניות, משיקים במשותף ל-C1,C2,C3.

קישורים חיצוניים

ויקישיתוף מדיה וקבצים בנושא ציר רדיקלי בוויקישיתוף
  • ציר רדיקלי, באתר MathWorld (באנגלית)
  • דוד פרייברט, חידושים בגאומטריה אוקלידית - תיאוריה של מרובע קמור ומעגל היוצר נקודות פסקל על צלעותיו, הוצאת אקדמון, 2021, נספח א'.

Read other articles:

County Lee, Alabama

Lee County, AlabamaCounty courthouse in OpelikaLokasi di negara bagian AlabamaLokasi negara bagian Alabama di Amerika SerikatDidirikanDecember 5, 1866SeatOpelikaKota terbesarAuburnWilayah • Keseluruhan616 sq mi (1.595 km2) • Daratan609 sq mi (1.577 km2) • Perairan7 sq mi (18 km2), 1.11%Populasi (est.) • (2007)130.516 • Kepadatan189/sq mi (73/km²)Situs webwww.leeco.us Lee County,...

 

Dok (maritim)

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Dok maritim – berita · surat kabar ...

 

جاي ليغ وينينغ إليفن 2008 كلوب شامبونشب

جاي ليغ وينينغ إليفن 2008 كلوب شامبونشب J-League Winning Eleven 2008 Club Championship Cover غلاف اللعبة المطور كونامي الناشر كونامي سلسلة اللعبة سلسلة وينينغ إليفن النظام بلاي ستيشن 2 تاریخ الإصدار 21 أغسطس 2008 اليابان نوع اللعبة لعبة رياضية النمط لعبة فرديةلعبة جماعية 8 لاعبين كحد أقصى الوسائط قرص...

Hum Hain Rahi Pyar Ke

Hum Hain Rahi Pyar KeSampul DVDNama lainहमHdzbg हैं राही प्यार केSutradaraMahesh BhattProduserTahir HussainSkenarioAamir KhanRobin Bhatt (juga Dialog)CeritaRobin Bhatt,Sujit SenPemeranAamir KhanJuhi ChawlaSharokh BharuchaKunal KhemuBaby AshrafaPenata musikLagu: Nadeem-Shravan Musik Latar: Shyam SurenderSinematograferPravin BhattPenyuntingSanjay SanklaPerusahaanproduksiTahir Hussain EnterprisesDistributorT. V. Films Pvt LtdTanggal rilis 23 Juli 1993&...

 

Joe Purcell

13th Lieutenant Governor of Arkansas Joe PurcellActing Governor of ArkansasIn officeJanuary 3, 1979 – January 9, 1979Preceded byDavid Pryoras GovernorSucceeded byBill Clintonas Governor13th Lieutenant Governor of ArkansasIn officeJanuary 14, 1975 – January 19, 1981GovernorDavid PryorBill ClintonPreceded byBob C. RileySucceeded byWinston Bryant45th Attorney General of ArkansasIn officeJanuary 10, 1967 – January 12, 1971GovernorWinthrop RockefellerPreceded byBru...

 

Daftar Wakil Bupati Ciamis

Wakil Bupati CiamisMahayunan ayuna kadatuan (Sunda) Siap menghadapi pembangunan guna mencapai kebahagiaan daerahPetahanaYana D. Putrasejak 20 April 2019Masa jabatan5 tahunDibentuk1993Pejabat pertamaDrs. H. Maman S. RachmanSitus webciamiskab.go.id Berikut ini adalah daftar pejabat Wakil Bupati Ciamis dari masa ke masa. No Portret Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 Drs. H.Maman S. Rachman 1993 1998 1   Brigadir Jenderal TNI (Purn.) Dr. Drs. H.Raden Dedem Ruchl...

Shorncliffe, Queensland

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) Suburb of Brisbane, Queensland, AustraliaShorncliffeBrisbane, QueenslandShorncliffe pier in the eveningShorncliffeCoordinates27°19′38″S 153°04′46″E / 27.3272°S 153.0794°E / -27.3272; 153.0794 (Shorncliffe (centre of suburb))Population1,870 (2016 census)[1] • Density1,250/km2 (3,230...

 

Deborah O'Neill

Australian politician SenatorDeborah O'NeillO'Neill in 2023Senator for New South WalesIncumbentAssumed office 13 November 2013Preceded byBob CarrMember of the Australian Parliamentfor RobertsonIn office21 August 2010 – 7 September 2013Preceded byBelinda NealSucceeded byLucy WicksVice President of the New South Wales Labor PartyIncumbentAssumed office 9 December 2011Serving with Mark BoydPresidentMark LennonLeaderKristina KeneallyJohn RobertsonLuke FoleyPreceded byTa...

 

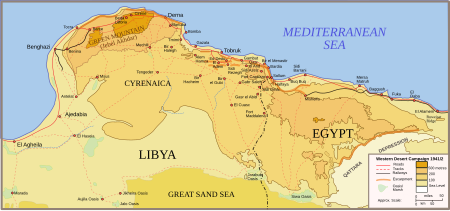
Invasi Mesir oleh Italia

Invasi Italia ke MesirBagian dari Kampanye Gurun Barat pada Perang Dunia KeduaGurun Barat 1940Tanggal9–16 September 1940LokasiMesir26°N 30°E / 26°N 30°E / 26; 30Koordinat: 26°N 30°E / 26°N 30°E / 26; 30Hasil InkonklusifPihak terlibat  Britania Raya Prancis Merdeka  Mesir  ItaliaTokoh dan pemimpin William Gott John Campbell Rodolfo Graziani Mario Berti Pietro MalettiKekuatan 2 brigade bersenjata205 pesawatDukungan an...

Древнедатский язык

Древнедатский язык Самоназвание dansk tunga Страны Дания Общее число говорящих 0 Статус Мёртвый язык Вымер в начале XVI века развился в датский язык Классификация Категория Языки Евразии Индоевропейская семья Германская ветвь Скандинавская группа Континентальная подгруппа ...

 

ロバート・デ・ニーロ

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日（80歳）出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット（1976年 - 1988年）グレイス・ハイタワー（1997年 - ）主な作品 『ミーン・ストリート』（1973年）...

 

Text-to-image model

Machine learning model An image conditioned on the prompt an astronaut riding a horse, by Hiroshige, generated by Stable Diffusion, a large-scale text-to-image model released in 2022 A text-to-image model is a machine learning model which takes an input natural language description and produces an image matching that description. Text-to-image models began to be developed in the mid-2010s during the beginnings of the AI boom, as a result of advances in deep neural networks. In 2022, the outpu...

Rotherham

Town in South Yorkshire, England For other uses, see Rotherham (disambiguation). This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (June 2023) (Learn how and when to remove this template message) Town in EnglandRotherhamTownTop to bottom, left to right: Rotherham Effingham Square, Bridge and Chapel, Town Hall, River Don Weir, Beeversleigh Flats and MinsterRotherhamLocation within South YorkshirePopulation109,691 (2011 cen...

 

Gabriel Jesus

Brazilian footballer (born 1997) Gabriel Jesus Gabriel Jesus with Brazil in 2018Personal informationFull name Gabriel Fernando de Jesus[1]Date of birth (1997-04-03) 3 April 1997 (age 27)[2]Place of birth São Paulo, BrazilHeight 1.75 m (5 ft 9 in)[3]Position(s) ForwardTeam informationCurrent team ArsenalNumber 9Youth career2010–2012 Anhanguera2013–2015 PalmeirasSenior career*Years Team Apps (Gls)2015–2017 Palmeiras 67 (21)2017–2022 Mancheste...

 

Masashi Hamauzu

Japanese composer and pianist (born 1971) Masashi Hamauzu浜渦 正志Hamauzu in 2012Born (1971-09-20) September 20, 1971 (age 52)Munich, West GermanyAlma materTokyo University of the ArtsOccupations Composer pianist lyricist Years active1996–presentMusical careerGenres Electronic classical ambient video game music Instrument(s)PianoWebsiteOfficial Website Musical artist Masashi Hamauzu (浜渦 正志, Hamauzu Masashi, born September 20, 1971) is a Japanese composer, pianist,...

土库曼斯坦总统

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

 

P. V. V. Lakshmi

Indian badminton player Badminton playerP. V. V. LakshmiPersonal informationCountryIndiaBorn (1974-11-08) 8 November 1974 (age 49)Vijayawada, Krishna District, Andhra Pradesh[1]ResidenceHyderabad, Telangana, IndiaHeight1.7 m (5 ft 7 in)[2]HandednessRight Medal record Representing  India Women's badminton Commonwealth Games 1998 Kuala Lumpur Women's team Pandimukkala Venkata Vara Lakshmi, better known as P. V. V. Lakshmi, is an India...

 

Spazio semplicemente connesso

Una possibile deformazione di una curva attorno alla sfera 2-dimensionale in un punto. In topologia, uno spazio topologico è semplicemente connesso se è connesso per archi e il suo gruppo fondamentale è il gruppo banale, ovvero se ogni curva chiusa può essere deformata fino a ridursi a un singolo punto. Più intuitivamente, uno spazio topologico è semplicemente connesso se è fatto di un pezzo solo e non ha buchi. Esempi di spazi semplicemente connessi sono la palla (con o senza la parte...

Škoda Transportation

Czech transport engineering company Not to be confused with the now-separate automobile manufacturer Škoda Auto or the former parent Škoda Works. Škoda Transportation a.s.Company typeJoint-stock companyIndustryRail transport machineryPredecessorŠkoda Works (founded 1859)Founded1995FounderEmil Škoda (as Škoda Works)HeadquartersPlzeň, Czech RepublicArea servedWorldwideKey peoplePetr Novotny (CEO) [1] Didier Pfleger Tomáš IgnačákMichal KoreckýProductselectric locomotivesmulti...

 

Artem Shmakov

Russian curler Artem ShmakovCurlerBorn (1990-03-06) March 6, 1990 (age 34)Chelyabinsk, RussiaTeamCurling clubAdamant CC, Saint PetersburgSkipArtem ShmakovThirdIvan KazachkovSecondAlexander PolushvaykoLeadDaniil ZazulskikhCurling career Member Association RussiaWorld Championshipappearances2 (2016, 2018)European Championshipappearances1 (2017)Other appearancesEuropean Junior Challenge: 1 (2011) Medal record Curling Russian Men's Championship 2013 Dmitrov 2014 Sochi 2015 Sochi 2012 Dm...