פירוק לערכים סינגולריים
|
Read other articles:

Guruh atau guntur adalah kata yang digunakan untuk mendeskripsikan gelombang kejut suara yang dihasilkan akibat terjadinya pemanasan dan pemuaian udara yang sangat cepat ketika dilewati oleh sambaran petir. Sambaran tersebut menyebabkan udara berubah menjadi plasma dan langsung meledak, menimbulkan munculnya suara yang bergemuruh. Fenomena ini terjadi pada saat bersamaan dengan kilatan petir, tetapi suara gemuruhnya biasanya terdengar beberapa saat setelah kilatan terlihat. Hal ini terjadi ka...

Adrianichthys Andrianichthys kruyti Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Beloniformes Famili: Adrianichthyidae Subfamili: AdrianichthyinaeWeber, 1913[1] Genus: AdrianichthysWeber, 1913 Spesies Lihat teks Adrianichthys adalah genus dalam famili Adrianichthyidae. Genus ini endemik di Danau Poso di Sulawesi, Indonesia dan semua spesies sangat terancam (dua spesies mungkin telah punah). Spesies Saat ini ada empat spesies yang diketahui dalam g...

Franjo Tuđman Airport Ltd.Zračna luka „Franjo Tuđman”IATA: ZAGICAO: LDZAInformasiJenisPublikPengelolaZLZMelayaniZagreb, KroasiaLokasiPleso, KroasiaMaskapai penghubungCroatia AirlinesKetinggian dpl108 mdplKoordinat45°44′35″N 016°04′08″E / 45.74306°N 16.06889°E / 45.74306; 16.06889Situs webwww.zagreb-airport.hrPetaZAGLokasi bandar udara di KroasiaLandasan pacu Arah Panjang Permukaan kaki m 05/23 10,669 3,252 Beton/Aspal Statistik (2011)Jumlah...

36 ← 35 36 37 → 数表 — 整数 << 30 31 32 33 34 35 36 37 38 39 >> 命名小寫三十六大寫參拾陸序數詞第三十六thirty-sixth識別種類整數性質質因數分解 {\displaystyle } 2 2 × 3 2 {\displaystyle 2^{2}\times 3^{2}} 表示方式值36算筹希腊数字ΛϚ´ 羅馬數字XXXVI 巴比伦数字𒌍𒐚 二进制100100(2)三进制1100(3)四进制210(4)五进制121(5)八进制44(8)十二进制...

Le financement de la vie politique et électorale en France fait l’objet d'un cadre législatif depuis la fin des années 1980. Les principales règles sont l’interdiction du financement politique par des personnalités morales et le plafonnement des dépenses électorales. L’État participe à la vie politique par le remboursement partiel des campagnes électorales, l’aide financière des partis politiques et des incitations fiscales pour le dons des particuliers aux partis. Les comp...

American politician (1754–1781) John Parke CustisPortrait of John Parke Custis by Charles Willson Peale, ca. 1774Member of the Virginia House of Delegates for Fairfax CountyIn officeMay 4, 1778 – March 22, 1781Serving with George MasonPreceded byPhilip AlexanderSucceeded byposition eliminated Personal detailsBornNovember 27, 1754White House Plantation,New Kent County,Virginia, British AmericaDiedNovember 5, 1781(1781-11-05) (aged 26)Eltham Plantation,New Kent County...

تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة استشهادات من مصادر موثوق بها. من الممكن التشكيك بالمعلومات غير المنسوبة إلى مصدر وإزالتها. (مايو 2018) شيربروك شعار الإحداثيات 45°24′N 71°54′W / 45.4°N 71.9°W / 45.4...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. لمعانٍ أخرى، طالع التنظيم (توضيح). التنظيم، هو فصيل مسلح تابع لحركة فتح أسسه مروان البرغوثي سنة 1995.[1][2][3] استقطب التنظيم العديد من الشباب وأصبح له عدة مكاتب ...

Giuseppe BertoLahir(1914-12-27)27 Desember 1914Mogliano Veneto, ItaliaMeninggal1 November 1978(1978-11-01) (umur 63)Roma, ItaliaPekerjaanNovelis dan penulis naskahTahun aktif1947–1978 Giuseppe Berto (27 Desember 1914 – 1 November 1978) adalah seorang penulis dan penulis naskah asal Italia. Ia dikenal karena membuat novel-novel berjudul Il cielo è rosso (The Sky Is Red) dan Il male oscuro. Filmografi pilihan Eleonora Duse (1947) La tua donna (1954) The Wanderers (...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bukit Tambun – news · newspapers · books · scholar · JSTOR (May 2017) (Learn how and when to remove this message) Suburb of Seberang Perai in Penang, MalaysiaBukit TambunSuburb of Seberang PeraiOthers transcription(s) • Mandarin武吉淡汶Buki...

Algerian Islamist leader Hassan HattabNative nameحسان حطابBorn14 January 1967Rouiba, AlgeriaAllegiance Algeria (?–1989) GIA (1992–1996) GSPC (1998–2003)RankEmirBattles/warsAlgerian Civil War Hassan Hattab (Arabic: حسان حطاب; born 14 January 1967), also known as Abu Hamza (Arabic: أبو حمزة), is the founder and first leader of the Algerian Jihadist rebel group Salafist Group for Preaching and Combat (GSPC) from 1998 to 2003. Early life and education Born in Rouiba o...

LuckyAlbum mini karya Weki MekiDirilis21 Februari 2018 (2018-02-21)GenreK-popDurasi18:13LabelFantagio MusicInterparkKronologi Weki Meki WEME(2017) Lucky(2018) Hide and Seek(2020) Singel dalam album Lucky La La LaDirilis: 21 Februari 2018 Video musikLa La La di YouTube Lucky adalah album mini kedua dari grup vokal wanita asal Korea Selatan Weki Meki. Album ini dirilis pada tanggal 21 Februari 2018, oleh Fantagio Music dan didistribusikan oleh Interpark. Album ini terdiri dari enam lag...

Castle in Gilan Province, Iran Chimarud castleقلعه چیمارودGeneral informationTypeCastleTown or cityRudbar CountyCountry IranChimarud castle (Persian: قلعه چیمارود) is a historical castle located in Rudbar County in Gilan Province, The longevity of this fortress dates back to the Nizari Ismaili state.[1][2] References ^ قلعه چیمارود یکی از زیباترین و قدیمی ترین اثار باستانی روستای تاریخی انبوه. ...

Берлинский филармонический оркестрBerliner Philharmoniker Берлинская филармония Основная информация Жанр классическая музыка Годы 1882 — наши дни Страна Германия Место создания Берлин Лейбл Дойче Граммофон Руководитель Кирилл Петренко Награды и премии медаль Карла Великого �...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Brythonic Celtic language spoken in Cornwall For the Cornish dialect and accent of English, see Cornish dialect. CornishKernewekKernowekPronunciation [kəɾˈnuːək] (Kernewek) [kəɾˈnɛʊək] (Kernewek) [kəɹˈnuːək] (Kernewek) [kəɹˈnɛʊək] (Kernewek) [kəɾˈnɔʊək] (Kernowek) [kəɹˈnɔʊək] (Kernowek) Native toUnited KingdomRegionCornwallEthnicityCornishExtinctEnd of 18th century[1][2][3][4]...

Coordination of multiple robots as a system This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (May 2016) (Learn how and when to remove thi...

Southernmost bridge crossing the San Francisco Bay Dumbarton BridgeThe Dumbarton Bridge and its adjacent powerline towersCoordinates37°30′25″N 122°07′01″W / 37.5069°N 122.1169°W / 37.5069; -122.1169Carries6 lanes of SR 84Bicycles and pedestriansCrossesSan Francisco BayLocaleMenlo Park, California and Fremont, CaliforniaOwnerState of CaliforniaMaintained byCalifornia Department of Transportation and the Bay Area Toll AuthorityWebsitewww.bayareafastrak.o...
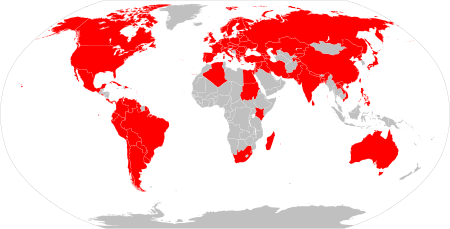
Questa voce o sezione sull'argomento partiti politici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Incontro Internazionale dei Partiti Comunisti e Operai(EN) International Meeting of Communist & Workers' Parties Stato Internazionale AbbreviazioneIMCWPSolidnet[2] Fondazione22 maggio 199...

سنتر هيل الإحداثيات 28°38′56″N 81°59′43″W / 28.648888888889°N 81.995277777778°W / 28.648888888889; -81.995277777778 [1] تاريخ التأسيس 1881 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة سومتر خصائص جغرافية المساحة 16.813488 كيلومتر مربع16.657668 كيلومتر مرب...












