פונקציה מחזורית
|
Read other articles:

Para el licor, véase Calvados (licor). Calvados Departamento BanderaEscudo Coordenadas 49°02′00″N 0°15′00″E / 49.033333333333, 0.25Capital CaenEntidad Departamento • País Francia • Número 14 • Región Normandía • Prefectura Caen • Subprefecturas BayeuxLisieuxVirePresidente del Consejo Anne d'Ornano (UDF)Subdivisiones Distritos 4Cantones 49Comunas 706Superficie Puesto 9.º • Total 5548 km²Población (2012) Pue...

У этого термина существуют и другие значения, см. Славянский базар (значения). Славянский базар в ВитебскеСлавянскі Базар у Віцебску Дата(ы) июль каждого года Место(а) проведения Белоруссия, Витебск Года с 1992 по настоящее время Жанр(ы) культуры стран мира Сайт fest-sbv.by Мед...

2011 Swedish filmShe MonkeysTheatrical release posterDirected byLisa AschanWritten byJosefine AdolfssonLisa AschanProduced byHelene LindholmStarringMathilda ParadeiserLinda MolinIsabella LindqvistCinematographyLinda WassbergEdited byKristofer NordinMusic bySami SänpäkkiläProductioncompanyAtmoDistributed byTriArt FilmRelease dates 31 January 2011 (2011-01-31) (Gothenburg Film Festival) 3 August 2011 (2011-08-03) (France) 2 September 2011 ...

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...

Television and movie studio in Hollywood Sunset Gower StudiosCompany typeIncentiveIndustryMediaEntertainmentFounded1912Headquarters1438 North Gower StreetHollywood, California90028ProductsTelevisionMovieWebsitewww.sunsetstudios.com/los-angeles/sound-stages-los-angeles/ Sunset Gower Studios is a 14-acre (57,000 m2) television and movie studio at the corner of Sunset Boulevard and North Gower Street in the Hollywood neighborhood of Los Angeles, California, United States. Established in 191...
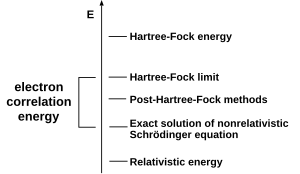
Kimia Kimia komputasi adalah cabang kimia yang menggunakan hasil kimia teori yang diterjemahkan ke dalam program komputer melalui simulasi komputer untuk menghitung sifat-sifat molekul dan perubahannya maupun melakukan simulasi terhadap sistem-sistem besar (makromolekul seperti protein atau sistem banyak molekul seperti gas, cairan, padatan, dan kristal cair), dan menerapkan program tersebut pada sistem kimia nyata. Contoh sifat-sifat molekul yang dihitung antara lain struktur (yaitu letak at...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

National League season This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 1895 Philadelphia Phillies season – news · newspapers · books · scholar · JSTOR (September 2021) The 1895 National League baseball season was the Philadelphia Phillies' third season as a team and their first training at the Nati...

Funiculaire de PauOverviewStatusOpenOwnerCity of PauLocalePau, FranceStations2HistoryOpened1907TechnicalLine length103 m (338 ft)Track gauge1,000 mm (3 ft 3+3⁄8 in)Maximum incline30% The railway from below Cars at the passing loop The upper station at night The Funiculaire de Pau, or Pau Funicular, is a funicular railway in the city of Pau in the Pyrénées-Atlantiques département of southwestern France. It links the Boulevard des Pyrénées, on the level ...

South Vietnamese military officer (1926–2023) Phạm Quốc ThuầnBorn(1926-08-31)August 31, 1926Hà Tây province, Tonkin, French IndochinaDiedAugust 18, 2023(2023-08-18) (aged 96)Fountain Valley, CaliforniaAllegiance State of Vietnam South Vietnam Service/branch Vietnamese National Army Army of the Republic of Vietnam RankLieutenant generalCommands held5th DivisionIII Corps Lieutenant General Pham Quoc Thuan (31 August 1926 – 18 August 2023) was an officer of the Army of the Repub...

Mass repressionin the Soviet Union Economic repression Collectivization Dekulakization Soviet famine of 1930–1933 Ukraine Kazakhstan Political repression Red Terror Purges of the Communist Party Great Purge Gulag Punitive psychiatry Ideological repression Religion 1917–1921 1921–1928 1928–1941 1958–1964 1975–1987 Christianity Islam Judaism Legislation Science Censorship Images Art Ethnic repression De-Cossackization National operations Population transfers Repressions of Poles Uk...

Institut Agama Islam Negeri KudusLogo Institut Agama Islam Negeri KudusNama lainIAIN KudusJenisPerguruan tinggi Islam negeri di IndonesiaDidirikan12 Dzulqaidah 1417 H / 21 Maret 1997 MLembaga indukKementerian Agama Republik IndonesiaAfiliasiIslamAkreditasiBAN-PT: Baik Sekali (2022–2027)[1]RektorProf. Dr. H. Abdurrohman Kasdi, Lc., M.Si.[2]AlamatJl. Conge, Ngembalrejo, Bae, Kudus, Jawa Tengah, IndonesiaWarna MerahSitus webwww.iainkudus.ac.id Institut Agama Islam Negeri ...

Never-opened train station in Manhattan, New York 59th StreetThe unused 59th Street station, 2021General informationLocationPark Avenue and 59th StreetUpper East Side, Manhattan, New YorkCoordinates40°45′47″N 73°58′11″W / 40.762941°N 73.969752°W / 40.762941; -73.969752Line(s)Park Avenue Tunnel (Hudson Line)Platforms2 side platformsTracks4 The 59th Street station is a never-opened station in the Park Avenue Tunnel used by the Metro-North Railroad. The statio...

Philippine government agency responsible for Metro Manila region Law enforcement agency Metropolitan Manila Development AuthorityPangasiwaan sa Pagpapaunlad ng Kalakhang Maynila (Filipino)AbbreviationMMDAMottoMarangal, Matapat, Disiplinado Ako[I am] Honorable, Honest, and DisciplinedAgency overviewFormedNovember 5, 1975; 48 years ago (1975-11-05)Annual budget₱4.78 billion (2020)[1]Jurisdictional structureOperations jurisdictionPhilippinesLegal jurisdictionMetr...
جزء من سلسلة مقالات حولعلم النفس تاريخ فروع خطوط عريضة المواضيع الرئيسية اللاقياسي السلوكي علم الوراثة السلوكي الحيوي المعرفي/معرفية المقارن عبر الثقافة الثقافي التنموي التمايزي التطوري التجريبي الحسابي العصبي الشخصية الإيجابي النفسي الديناميكي القياس النفسي الكمي ال...

Untuk nama belakang, lihat Schlumberger (nama belakang). Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Schlumberger. Contoh paragraf pembuka Schlumberger adalah .... (April 2021) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Schlumberger LimitedJenisPublikKode emitenNYSE: SLBKomponen S&P 100Komponen S&P 500ISINAN8068571086IndustriJasa dan per...
Unincorporated community in New Mexico, United StatesMiami, New MexicoUnincorporated communityMiamiLocation within the state of New MexicoShow map of New MexicoMiamiMiami (the United States)Show map of the United StatesCoordinates: 36°21′00″N 104°47′35″W / 36.35000°N 104.79306°W / 36.35000; -104.79306CountryUnited StatesStateNew MexicoCountyColfaxElevation[1]6,195 ft (1,888 m)Time zoneUTC-7 (Mountain (MST)) • Summer (DST)UTC-6...

Reinhard Genzel Premio Nobel per la fisica 2020 Reinhard Genzel (Bad Homburg vor der Höhe, 24 marzo 1952) è un astrofisico tedesco, che ha dato contributi decisivi nei campi dell'astronomia dell'infrarosso e submillimetrica, dell'imaging astronomico ad alta definizione, nello studio del Centro della Via Lattea, dei buchi neri supermassicci nel centro delle galassie, dei meccanismi di formazione ed evoluzione galattica e dei fenomeni di formazione stellare. Nel 2020 ha condiviso con Roge...

この項目では、ポーランドの都市について説明しています。同市にある銃器メーカーの通称ラドム造兵廠については「ファブルィカ・ブローニ・ウーチュニク」をご覧ください。 Radom City hall, Cathedral of Virgin Mary, Office of City, Official logo, Orlik Aerobatic Team, Market Square, Museum of the Radom Village 紋章 Radom 北緯51度24分 東経21度10分 / 北緯51.400度 東経21.167度 / 51.400; 2...

اضغط هنا للاطلاع على كيفية قراءة التصنيف قوقع أصفر المرتبة التصنيفية نوع التصنيف العلمي فوق النطاق حيويات مملكة عليا حقيقيات النوى مملكة فطر عويلم ثنائيات النوى شعبة دعاميات كتيبة غاريقونينية طائفة غاريقونانية رتبة كويزيات فصيلة ...
























![{\displaystyle \ f(x)=x-[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc799ae459b11f64aea0e340ad6eb8d534628c)
![{\displaystyle \ [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/325f8129ef4954f7f475b04e33cc996ef077dd52)