משפט הלדר (תורת החבורות)
|
Read other articles:

Cet article est une ébauche concernant le droit français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Article 68-1 de la Constitution du 4 octobre 1958 Données clés Présentation Pays France Langue(s) officielle(s) Français Type Article de la Constitution Adoption et entrée en vigueur Législature Xe législature de la Cinquième République française Gouvernement Édouard Balladur Promulgation 27 jui...

Ice hockey stadium in Czechia This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: ČEZ Stadion – news · newspapers · books · scholar · JSTOR (October 2010) (Learn how and when to remove this template message) ČEZ StadionFormer namesZimní stadionLocationHokejových legend 2531, Kladno, Czech Republic 272 01Coordinates50°08′14...

Private graduate school in Ontario, Canada 43°39′30.15″N 79°23′51.03″W / 43.6583750°N 79.3975083°W / 43.6583750; -79.3975083 Institute for Christian StudiesTypePrivateEstablished1967; 57 years ago (1967)PresidentRonald A. KuipersAcademic staff8[1]LocationToronto, Ontario, CanadaCampusUrban, distanceColoursWhite, redNicknameICSAffiliationsTST, INCHEWebsitewww.icscanada.edu The Institute for Christian Studies (ICS or ICS Toronto) is ...

Television channel in the Netherlands Television channel NPO 2CountryNetherlandsBroadcast areaNational. Also available in Belgium and Germany.HeadquartersHilversumProgrammingLanguage(s)DutchPicture format1080p HDTV(downscaled to 16:9 576i for the SDTV feed)OwnershipOwnerNPOSister channelsNPO 1NPO 3NPO 1 ExtraNPO 2 ExtraNPO Politiek en NieuwsHistoryLaunched1 October 1964; 59 years ago (1964-10-01)Former namesNederland 2 (1964–1990, 2000–2014)TV2 (1990–2000)LinksWebsiteN...

This is an archive of past discussions. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. Archive 40 ← Archive 44 Archive 45 Archive 46 Archive 47 Archive 48 → Archive 50 Category:GLAAD Media Award winners Category:GLAAD Media Award winners has been nominated for deletion -- 70.24.244.158 (talk) 06:16, 5 September 2013 (UTC) Daniel Kawczynski Daniel Kawczynski (edit | talk | history | protect...

Pour les articles homonymes, voir Paiva (homonymie). Adriano de PaivaBiographieNaissance 1847BragaDécès 1907PortoNationalité portugaiseActivités Physicien, homme politiquemodifier - modifier le code - modifier Wikidata Adriano de Paiva (1847-1907) est un pionnier portugais de la recherche sur la télévision. Biographie Professeur de physique à l'Université de Porto, Il est parmi les premiers à avoir imaginé la télévision et a travaillé notamment sur les propriétés de photocondu...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Putut Eko Bayu SenoPutut Eko Bayuseno saat menjabat sebagai Kepala Kepolisian Daerah Metro Jaya (2012) Inspektur Pengawasan Umum PolriMasa jabatan13 September 2017 – 26 April 2019PendahuluDwi PriyatnoPenggantiMoechgiyartoKepala Badan Pemelihara Keamanan PolriMasa jabatan18 Maret 2014 – 13 September 2017PendahuluBadrodin HaitiPenggantiMoechgiyartoKepala Kepolisian Daerah Metropolitan Jakarta Raya ke–31Masa jabatan31 Oktober 2012 – 18 Maret 2014PendahuluUn...

Species of snake This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Borneo python – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this template message) Not to be confused with Sumatran short-tailed python or Blood python. Borneo python Conservation status Least Concer...
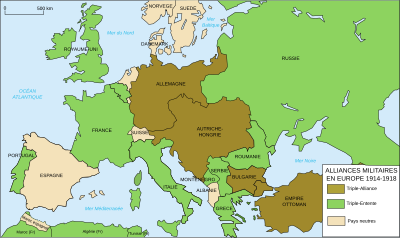
Pour les articles homonymes, voir Triple alliance. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juin 2018). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratiq...

D'Estienne d'Orves-class aviso of the French Navy Premier-Maître L'Her History France NamePremier-Maître L'Her NamesakePremier-Maître L'Her BuilderArsenal de Lorient, Lorient Laid down15 December 1978 Launched28 June 1980 Commissioned15 December 1981 DecommissionedExpected, 2024 HomeportBrest[1] Identification Callsign: FAPM Pennant number: F792 StatusActive General characteristics Class and typeD'Estienne d'Orves-class aviso Displacement 1,100 t (1,100 long tons) standard 1,2...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chai Shao – news · newspapers · books · scholar · JSTOR (August 2013) (Learn how and when to remove this me...

West Indian cricketer Rolph GrantRolph Grant in 1939Personal informationFull nameRolph Stewart GrantBorn(1909-12-15)15 December 1909Port of Spain, TrinidadDied18 October 1977(1977-10-18) (aged 67)Oakville, Ontario, CanadaBattingRight-handedBowlingRight arm off breakRelationsFred Grant (brother)Lindsay Grant (brother)Jackie Grant (brother)International information National sideWest IndiesTest debut (cap 39)8 January 1935 v EnglandLast Test19 August 1939 v ...

Иеракиты в книге В. Н. Бенешевича Древнеславянская кормчая XIV титулов без толкования. СПб, 1907. Т. 1. Иераки́ты (др.-греч. ἱερακῖται; др.-рус. иєракитє) — ересь или секта, описанная в конце IV века Епифанием в «Панарионе» в числе 80 ересей и Иоанном Дамаскиным в книге «О с�...

Cet article est une ébauche concernant une localité du New Jersey. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. MaplewoodGéographiePays États-UnisÉtat New JerseyComté comté d'EssexSuperficie 10,05 km2Altitude 69 mCoordonnées 40° 43′ 44″ N, 74° 16′ 05″ ODémographiePopulation 25 684 hab. (2020)Densité 2 555,6 hab./km2 (2020)Fonctionnement...

Study of processing speed on cognitive tasks Representation of the stages of processing in a typical reaction time paradigm Mental chronometry is the scientific study of processing speed or reaction time on cognitive tasks to infer the content, duration, and temporal sequencing of mental operations. Reaction time (RT; also referred to as response time) is measured by the elapsed time between stimulus onset and an individual's response on elementary cognitive tasks (ECTs), which are relatively...

Election for the governor of North Dakota For related races, see 1960 United States gubernatorial elections. 1960 North Dakota gubernatorial election ← 1958 November 8, 1960 1962 → Nominee William L. Guy Clarence P. Dahl Herschel Lashkowitz Party Democratic–NPL Republican Independent Popular vote 136,148 122,486 16,741 Percentage 49.44% 44.48% 6.08% County resultsGuy: 40–50% 50–60% ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2019) منتخب غانا لدوري الرغبي بلد الرياضة غانا أكبر فوز أكبر خسارة تعديل مصدري - ت�...

سنطورمعلومات عامةتصنيف آلة وترية نقرية — آلة إيقاعية هورنبوستيل-ساكس 314.122-4 مجال العزفمقطع صوتيتعديل - تعديل مصدري - تعديل ويكي بيانات السنطور[1][2][3] أو السنطير[1][3] (من الفارسية: سنتور)[1] هي من الآلات الموسيقية الشرقية، لها وجهين، السفلي أكبر من وجهه�...

Place in White Carniola, SloveniaTušev DolTušev DolLocation in SloveniaCoordinates: 45°35′1.77″N 15°9′1.08″E / 45.5838250°N 15.1503000°E / 45.5838250; 15.1503000Country SloveniaTraditional regionWhite CarniolaStatistical regionSoutheast SloveniaMunicipalityČrnomeljArea • Total0.72 km2 (0.28 sq mi)Elevation192.4 m (631.2 ft)Population (2020) • Total77 • Density110/km2 (280/sq mi)[1...



















