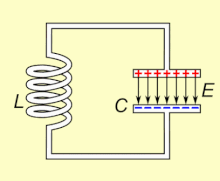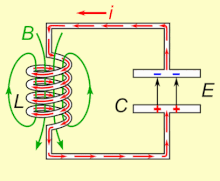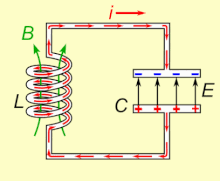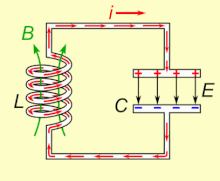
„Ю„Ґ„Т„Ь LC
|
Read other articles:

–≠–ї–µ–Ї—В—А–Њ–љ (–Ї—А–∞—Б–љ–∞—П —З–∞—Б—В–Є—Ж–∞), –њ–∞–і–∞—О—Й–Є–є –љ–∞ –≥—А–∞–љ–Є—Ж—Г –Љ–µ–ґ–і—Г –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ –њ—А–Њ–≤–Њ–і–љ–Є–Ї–Њ–Љ (N) –Є —Б–≤–µ—А—Е–њ—А–Њ–≤–Њ–і–љ–Є–Ї–Њ–Љ (S), —Б–Њ–Ј–і–∞—С—В –Ї—Г–њ–µ—А–Њ–≤—Б–Ї—Г—О –њ–∞—А—Г –≤ —Б–≤–µ—А—Е–њ—А–Њ–≤–Њ–і–љ–Є–Ї–µ –Є –Њ—В—А–∞–ґ–∞–µ—В—Б—П –Њ–±—А–∞—В–љ–Њ –≤ –≤–Є–і–µ –і—Л—А–Ї–Є (–Ј–µ–ї—С–љ–∞—П —З–∞—Б—В–Є—Ж–∞) –≤ –Њ–±—Л—З–љ—Л–є –њ—А–Њ–≤–Њ–і–љ–Є–Ї. –Т–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —Б—В—А–µ–ї–Ї–Є –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В –Њ—А–Є–µ–љ—В–∞—Ж–Є—О —Б–њ–Є–љ–∞. –Рпњљ...

Yeongnam Air IATA ICAO Kode panggil OE ONA YEONGNAM AIR DidirikanJul. 2008Berhenti beroperasiDec. 2008PenghubungBandar Udara Internasional GimhaeKota fokusBusan,DaeguArmada1Tujuan4SloganLet's fly for the future!Kantor pusat Busan, Korea SelatanTokoh utamaByong Hun, OhSitus webhttp://www.ynair.co.kr/ Yeongnam Air (Yeongnam Eeo мШБлВ®мЧРмЦі) adalah sebuah maskapai penerbangan regional di Korea Selatan. Basis utama untuk penerbangan Yeongnam Air terletak di Bandar Udara Internasional Gimhae dan ...

South Korean satellite Koreasat 7ArianespaceMission typeCommunications SatelliteOperatorKT SatCOSPAR ID2017-023A SATCAT no.42691 Spacecraft propertiesBusSpacebus-4000B2[1]ManufacturerThales Alenia Space Start of missionLaunch date00:00, April 5, 2017 (UTC) (2017-04-05T00:00Z) UTCRocketArianespace Orbital parametersReference systemGeocentricRegimeGeosynchronousLongitude116° E TranspondersBandKu, KaCoverage areaKorea, Philippines, Indonesia, India ...

Pour les articles homonymes, voir Derni√®res Nouvelles (homonymie) et DNA. Derni√®res Nouvelles d'Alsace DNA Pays France Langue Fran√Іais P√©riodicit√© Quotidien Genre G√©n√©raliste r√©gional Prix au num√©ro 1,10 вВђ Diffusion 134 197[1] ex. (2018/2019) Fondateur Heinrich Ludwig Kayser Date de fondation 1877 √Йditeur Derni√®res Nouvelles d'Alsace Ville dвАЩ√©dition Strasbourg Propri√©taire Cr√©dit Mutuel via EBRA Directeur de publication Laurent Couronne R√©dacteur en chef Fr√©d√©ric V√©zard...

Raini RodriguezLahir1 Juli 1993 (umur 30)[1]Bryan, Texas, U.S.[2]PekerjaanActress and singerTahun aktif2006вАУsekarang Raini Rodriguez (lahir 1 Juli 1993)[1] adalah seorang aktris dan penyanyi Amerika Serikat Filmografi Acting Year Film/Series Role Other notes 2006 Huff Denise Black Shadows (Season 2, episode 12) 2007 Handy Manny Isabel Montoya Lost and Found; voice role 2007 Family of the Year Maria Pilot (Season 1, episode 1) The Suite Life of Zack & C...

Tentara Panzer ke-22. Panzerarmeecode: de is deprecated InsigniaAktif5 Juni 1940 вАУ 8 Mei 1945Negara Nazi GermanyCabangTentara WehrmachtTipe unitPanzerPeranPeperangan lapis bajaJumlah personelAngkatan BersenjataPertempuranPerang Dunia II Front Timur TokohTokoh berjasaHeinz Guderian Tentara Panzer ke-2 (Jerman: 2. Panzerarmeecode: de is deprecated ) adalah formasi kendaraan lapis baja Jerman Nazi selama Perang Dunia II yang dibentuk dari Grup Panzer ke-2 pada tanggal 5 Oktober 1941. Grup...

Satelit kota Wigan Wigan merupakan nama kota di Inggris. Letaknya di bagian barat. Tepatnya di County Greater Manchester, Inggris. Pada tahun 2001, kota ini memiliki jumlah penduduk sebanyak 81.203 jiwa. Lihat pula Wigan Rural District Pranala luar Wigan Council Diarsipkan 2005-12-03 di Wayback Machine. Artikel bertopik geografi atau tempat Inggris ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Medical discipline for preventing nosocomial or healthcare-associated infection Infection prevention and control is the discipline concerned with preventing healthcare-associated infections; a practical rather than academic sub-discipline of epidemiology. In Northern Europe, infection prevention and control is expanded from healthcare into a component in public health, known as infection protection (smittevern, smittskydd, Infektionsschutz in the local languages). It is an essential part of t...

Saint-√Йtienne-sur-Suippecomune Saint-√Йtienne-sur-Suippe вАУ Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementReims CantoneBourgogne TerritorioCoordinate49¬∞23вА≤N 4¬∞06вА≤E / 49.383333¬∞N 4.1¬∞E49.383333; 4.1пїњ (Saint-√Йtienne-sur-Suippe)Coordinate: 49¬∞23вА≤N 4¬∞06вА≤E / 49.383333¬∞N 4.1¬∞E49.383333; 4.1пїњ (Saint-√Йtienne-sur-Suippe) Superficie7,66 km¬≤ Abitanti283[1] (2009) Densit√†36,95 ab./km¬≤ Al...

Hubble Space TelescopeEmblema missione Immagine del veicoloIl telescopio spaziale Hubble visto dallo Space Shuttle Atlantis, durante la missione di servizio 4 (STS-125), la sesta e ultima Dati della missioneOperatoreNASA/STScI NSSDC ID1990-037B SCN20580 Satellite diTerra Esitoin corso ShuttleDiscovery VettoreSpace Shuttle Discovery (STS-31) Lancio24 aprile 1990 Luogo lancioRampa 39B Durata33 anni e 6 mesi (in corso) Proprietà del veicolo spazialePotenza2800 watt Massa11110 kg Costr...

Pour les articles homonymes, voir Hess. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mai 2008). Si vous disposez d'ouvrages ou d'articles de r√©f√©rence ou si vous connaissez des sites web de qualit√© traitant du th√®me abord√© ici, merci de compl√©ter l'article en donnant les r√©f√©rences utiles √† sa v√©rifiabilit√© et en les liant √† la section ¬Ђ Notes et r√©f√©rences ¬ї. En pratique : Qu...

Regional campus of Rutgers University in Camden, New Jersey, US This article is about Rutgers University's campus in Camden, New Jersey. For the university as a whole, see Rutgers University. For other uses of Rutgers, see Rutgers (disambiguation). RutgersThe State University of New JerseyCamdenOfficial Seal of Rutgers UniversityFormer namesSouth Jersey Law School (1926вАУ1927)College of South Jersey (1927вАУ1950)Rutgers College of South Jersey (1950вАУ1970)[1]MottoSol iustitiae et oc...

Elezioni parlamentari in Ucraina del 1994 Stato Ucraina Data 27 marzo (primo turno), 2-10 aprile (secondo turno) Assemblea Verchovna Rada Liste KPU NRU SPU Voti 3.683.33212,72%% 1.491.1645,15% 895.8303,09% Seggi 86 / 450 20 / 450 14 / 450 Distribuzione dei seggi per regione 1990 1998 Le elezioni parlamentari in Ucraina del 1994 si tennero il 27 marzo (primo turno) e il 2 e 10 aprile (secondo turno). Le elezioni furono indette in seguito ad un accordo fra il Presidente e il Parlamento: ...

Play written by Ben Travers Aldwych company in Thark (1927). From left: Mary Brough, Ralph Lynn, Winifred Shotter, Robertson Hare, Tom Walls, Ethel Coleridge and Gordon James Thark is a farce by the English playwright Ben Travers. It was first given at the Aldwych Theatre, London, the fourth in the series of twelve Aldwych farces presented at the theatre by the actor-manager Tom Walls between 1923 and 1933. It starred the same cast members as many of the other Aldwych farces. The story concer...

Evan Longoria (2008) is the only Rays' first-round pick to win a Rookie of the Year Award with the team. The Tampa Bay Rays are a Major League Baseball franchise based in St. Petersburg, Florida. The Rays (formerly the Tampa Bay Devil Rays) compete in the American League East division. Since the franchise was established in 1995, the Rays have selected 36 players in the first round. Officially known as the First-Year Player Draft,[1] the Rule 4 Draft is Major League Baseball's primar...

иК±еЉПжТЮзРГзЪДзРГжЮ± иК±еЉПжТЮзРГпЉИиЛ±и™ЮпЉЪPoolпЉЙпЉМжШѓжТЮзРГйБЛеЛХзЪДдЄАз®Ѓй°ЮеЮЛпЉМдљњзФ®жЬЙеЕ≠еАЛзРГиҐЛзЪДзРГж°МпЉМдї•жУКзРГеЕ•иҐЛзВЇдЄїи¶БзЫЃзЪДгАВ[1][2]иК±еЉПжТЮзРГжЬЙеЊИе§ЪдЄНеРМзЪДзО©ж≥ХпЉМжѓПеАЛйГљжЬЙеЕґзЙєеЃЪзЪДеРНз®±пЉЫдЄАдЇЫжѓФиЉГзЯ•еРНзЪДеМЕжЛђ8иЩЯзРГгАБиЛ±еЉП8иЩЯзРГеПКеЕґиЃКйЂФйїСзРГгАБ9иЩЯзРГгАБ10иЩЯзРГгАБ7иЩЯзРГгАБ14.1гАБдЄАиҐЛзРГеТМзБМиҐЛжТЮзРГпЉИиЛ±иѓ≠пЉЪBank poolпЉЙгАВ йАЪзФ®и°Уи™ЮгАМиРљиҐЛжТЮзРГгАНжЬЙжЩВдєЯ襀䚜зФ®пЉМдЄ¶дЄФеПЧеИ∞дЄАдЇЫиК±еЉПжТЮзРГж•≠иАЕ...

дєФеЖ†еНО дЄ≠еНОдЇЇж∞СеЕ±еТМеЫље§ЦдЇ§йГ®йГ®йХњ дЄ≠еЫљдЇЇж∞Сеѓєе§ЦеПЛе•љеНПдЉЪй°ЊйЧЃ дїїжЬЯ1974еєі11жЬИвАФ1976еєі12жЬИжАїзРЖеС®жБ©жЭ• вЖТ еНОеЫљйФЛеЙНдїїеІђйєПй£ЮзїІдїїйїДеНО дЄ™дЇЇиµДжЦЩжАІеИЂзФЈеЗЇзФЯ(1913-03-28)1913еєі3жЬИ28жЧ• дЄ≠иПѓж∞СеЬЛж±ЯиШЗзЬБзЫРеЯОеОњйАЭдЄЦ1983еєі9жЬИ22жЧ•(1983ж≠≤вАФ09вАФ22)пЉИ70ж≠≤пЉЙ дЄ≠еНОдЇЇж∞СеЕ±еТМеЫљеМЧдЇђеЄВз±Ниіѓж±ЯиШЗйєљеЯОеЫљз±Н дЄ≠еНОдЇЇж∞СеЕ±еТМеЫљжФњеЕЪ дЄ≠еЫљеЕ±дЇІеЕЪйЕНеБґжШОдїБпЉИ1940еєізЧЕйАЭпЉЙ йЊЪжЊОпЉИ1970еєізЧЕйАЭпЉЙ зЂ†еРЂпњљ...

Jamaican ChristiansTotal populationapprox. 1,960,000ReligionsBaptist, Seventh-day Adventist, Roman Catholic, AnglicanLanguagesMain languages spoken are English and Jamaican Patois. The Anglican St. Jago de la Vega Cathedral, Spanish Town, Jamaica. Christianity was introduced by Spanish settlers who arrived in Jamaica in 1509. Thus, Roman Catholicism was the first Christian denomination to be established. Later, Protestant missions were very active, especially the Baptists, and played a key r...

ЎђўЕЎєўКЎ© ЎІўДЎ™ЎђўЕЎє ЎІўДўВўИўЕўК ЎІўДЎѓўКўЕўВЎ±ЎІЎЈўК ЎІўДЎ®ўДЎѓ ЎІўДЎ®Ў≠Ў±ўКўЖ ЎІўДЎ™Ў£Ў≥ўКЎ≥ Ў™ЎІЎ±ўКЎЃ ЎІўДЎ™Ў£Ў≥ўКЎ≥ 1991 ЎІўДўЕЎ§Ў≥Ў≥ўИўЖ Ў≠Ў≥ўЖ ЎєўДўК ЎІўДўЕўВЎ± ЎІўДЎ±Ў¶ўКЎ≥ўК ЎІўДЎ≤ўЖЎђ ўЕўВЎ± ЎІўДЎ≠Ў≤Ў® ЎІўДЎ≤ўЖЎђ[1] ЎІўДЎ£ўБўГЎІЎ± ЎІўДЎ£ўКЎѓўКўИўДўИЎђўКЎІ ЎІўДЎ®ЎєЎЂўКЎ© ЎІўДЎђЎѓўКЎѓЎ©ЎІўДЎµЎѓЎІўЕўКЎ© ЎІўЖЎ™Ў≥ЎІЎ® ЎѓўИўДўК Ў≠Ў≤Ў® ЎІўДЎ®ЎєЎЂ (ЎІўДўБЎµўКўД ЎІўДўЕўЗўКўЕўЖ ЎєўДўКўЗ ЎєЎ±ЎІўВўКЎІ) ЎІўДўЕЎіЎІЎ±ўГЎ© ўБўК ЎІўДЎ≠ўГўЕ ЎєЎѓЎѓ ЎІўДўЖўИЎІЎ® 0 ўЕЎђўДЎ≥ ЎІўД...

Disney-ABC International TelevisionJenisSwasta (subsidiari dari The Walt Disney Company)Didirikan1985KantorpusatBurbank, Kalifornia, Amerika SerikatWilayah operasiInternasionalPemilikThe Walt Disney CompanyIndukDisney-ABC Television Group Disney-ABC International Television (DAIT) adalah sebuah perusahaan yang mendistribusikan film dari The Walt Disney Company. Disney-ABC International Television juga memiliki lisensi untuk mendistribusikan film dari: Walt Disney Pictures Touchstone Pictures ...