חפיפ×ھ ××کריצו×ھ
| ||||||
Read other articles:

Kebun Botani SingapuraDanau SimponiLokasi di SingapuraLokasiSingapuraKoordinat1آ°18′30″N 103آ°49′04″E / 1.3084163976678724آ°N 103.81786005678232آ°E / 1.3084163976678724; 103.81786005678232Koordinat: 1آ°18′30″N 103آ°49′04″E / 1.3084163976678724آ°N 103.81786005678232آ°E / 1.3084163976678724; 103.81786005678232Area74 hektare (182,86 ekar)Dibuat1859 (1859) Kebun Botani SingapuraSitus Warisan Dunia UNESCOKriteriaAlam: ii, iv...

Animated televisionseries By decade 1948–1969 Pre-1960 1960s 1970s 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000s 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010s 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020s 2020 2021 2022 2023 2024 vte These are lists of animated television series first aired in the 2020s, organized by year: List of animated television...

American politician Charles Forest Nelson PrattCharles Forest Nelson Pratt Massachusetts House of Representatives 1929Member of the Massachusetts House of Representativesfrom the 10th Essex districtIn office1927–1935Preceded byHarriet Russell HartSucceeded byWilliam Landergan Personal detailsBornFebruary 4, 1891Saugus, MassachusettsDiedNovember 5, 1968 (aged 77)Saugus General HospitalSaugus, MassachusettsPolitical partyRepublicanEducationSaugus High SchoolNortheastern University...

ط§ظ„ظ‚ظˆط§طھ ط§ظ„ظ…ط³ظ„طط© ط§ظ„ظƒط±ظˆط§طھظٹط© ط´ط¹ط§ط± ط§ظ„ظ‚ظˆط§طھ ط§ظ„ظ…ط³ظ„طط© ط§ظ„ظˆط·ظ†ظٹط© ظپظٹ ظƒط±ظˆط§طھظٹط§ط´ط¹ط§ط± ط§ظ„ظ‚ظˆط§طھ ط§ظ„ظ…ط³ظ„طط© ط§ظ„ظˆط·ظ†ظٹط© ظپظٹ ظƒط±ظˆط§طھظٹط§ ط§ظ„ط¯ظˆظ„ط© ظƒط±ظˆط§طھظٹط§ ط§ظ„طھط£ط³ظٹط³ 26 ط³ط¨طھظ…ط¨ط± 1991 ط§ط³ظ… ط¢ط®ط± ط§ظ„ط¬ظٹط´ ط§ظ„ظپط±ظˆط¹ ط§ظ„ظ‚ظˆط§طھ ط§ظ„ط¨ط±ظٹط© ط§ظ„ظ‚ظˆط§طھ ط§ظ„ط¨طط±ظٹط© ط§ظ„ظ‚ظˆط§طھ ط§ظ„ط¬ظˆظٹط© ط§ظ„ط§ط´طھط¨ط§ظƒط§طھ طط±ط¨ ط§ظ„ط§ط³طھظ‚ظ„ط§ظ„ ط§ظ„ظƒط±ظˆط§طھظٹط©طŒ ظˆطط±ط¨ ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ...

Mythical source of silver in South America This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sierra de la Plata – news آ· newspapers آ· books آ· scholar آ· JSTOR (June 2015) (Learn how and when to remove this template message) Cerro Rico de Potosأ as depicted in 1715, the possible origin of the Sierra de la Plata...

Wu BinPortrait du Bouddha du peintre Wu Bin. (1573-1620).BiographieNaissance 1573Putian (Xinghua Fu (d), Fujian (d), dynastie Ming)Dأ©cأ¨s 1620Activitأ©s Peintre, أ©crivain, poأ¨teAutres informationsGenre artistique Paysagemodifier - modifier le code - modifier Wikidata Wu Bin هگ´ه½¬ (peintre) ou Wou Pin ou Wu Pin, surnom: Wenzhong, nom de pinceau: Zhixian, originaire de Putian, province du Fujian. XVIe – XVIIe siأ¨cles. Actif أ la cour pendant l'أ¨re Waanli (1573-1620). Chinois. ...

Voce principale: Real Club Celta de Vigo. Real Club Celta de VigoStagione 2021-2022Sport calcio Squadra Celta Vigo Allenatore Eduardo Coudet Presidente Carlos Mouriأ±o Primera Divisiأ³n11آ؛ Coppa del ReSedicesimi di finale Maggiori presenzeCampionato: D. Suأ،rez, Dituro (38)Totale: D. Suأ،rez, B. Mأ©ndez (40) Miglior marcatoreCampionato: Iago Aspas (18)Totale: Iago Aspas (18) StadioStadio Balaأdos (35 000 posti) Maggior numero di spettatori13 146 vs Barcellona (6 novembre 202...

Instalasi fondasi dalam untuk sebuah jembatan di Napa, California, Amerika Serikat. Fondasi dalam adalah jenis fondasi dibedakan dari fondasi dangkal dengan kedalaman mereka tertanam ke dalam tanah. Ada banyak alasan seorang insinyur geoteknik akan merekomendasikan fondasi dalam ke fondasi dangkal, tetapi beberapa alasan umum adalah beban desain yang sangat besar, tanah yang buruk pada kedalaman dangkal, atau kendala situs (seperti garis properti). Ada istilah yang berbeda digunakan untuk men...

Subfamily of primates Perodicticinae Calabar angwantibo, Arctocebus calabarensis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Strepsirrhini Family: Lorisidae Subfamily: PerodicticinaeGray, 1870 Genera Perodicticus Arctocebus Perodicticinae is a subfamily of the family Lorisidae. It includes five species of African primates as shown under taxonomy below. They have a vestigial tail and index finger. The snout is pointed...
2020ه¹´ه¤ڈه£ه¥¥و—هŒ¹ه…‹è؟گهٹ¨ن¼ڑو³¢ه…°ن»£è،¨هœکو³¢ه…°ه›½و——IOC編碼POLNOCو³¢èکه¥§و—هŒ¹ه…‹ه§”ه“،وœƒç¶²ç«™olimpijski.pl(英و–‡ï¼‰ï¼ˆو³¢ه…°و–‡ï¼‰2020ه¹´ه¤ڈه£ه¥¥و—هŒ¹ه…‹è؟گهٹ¨ن¼ڑ(و±ن؛¬ï¼‰2021ه¹´7وœˆ23و—¥è‡³8وœˆ8و—¥ï¼ˆهڈ—2019ه† çٹ¶ç—…و¯’ç—…ç–«وƒ…ه½±ه“چوژ¨è؟ں,ن½†ن»چن؟ç•™هژںه®ڑهگچ称)éپ‹ه‹•ه“،206هڈƒè³½é …ç›®24ن¸ھه¤§é،¹و——و‰‹ه¼€ه¹•ه¼ڈï¼ڑه¸•ç»´ه°”آ·ç§‘çƒه°¼ه¥¥ه¤«و–¯هں؛(و¸¸و³³ï¼‰ه’Œé©¬ه¨…آ·و²ƒن»€ن¹”ه¤«و–¯هچ،(è‡ھè،Œè½¦ï¼‰[1]é—ه¹•ه¼ڈï¼ڑهچ،ç½—هˆ©ه¨œآ·ç؛³ن؛ڑ(çڑ®هˆ’艇)&#...

You can help expand this article with text translated from the corresponding article in French. (October 2009) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipe...

En sociologأa y psicologأa social, la confianza es la creencia en que una persona o grupo serأ، capaz y desearأ، actuar de manera adecuada en una determinada situaciأ³n y pensamientos. La confianza se verأ، mأ،s o menos reforzada en funciأ³n de las acciones y de valores. La confianza es una hipأ³tesis sobre la conducta futura del otro. Es una actitud que concierne el futuro, en la medida en que este futuro depende de la acciأ³n de un otro. Es una especie de apuesta que consiste en no inqui...

Danau TambingRano Kalimpaa Danau Tambing pada bulan Oktober 2016 Lokasi di Sulawesi Informasi Lokasi Sedoa, Lore Utara, Kabupaten Poso Negara Indonesia Koordinat 1آ°11′S 120آ°11′E / 1.19آ°S 120.18آ°E / -1.19; 120.18Koordinat: 1آ°11′S 120آ°11′E / 1.19آ°S 120.18آ°E / -1.19; 120.18 Pemilik Jenis objek wisata Wisata alam Danau Tambing (bahasa Pamona: Rano Kalimpaa, Rano Tambing), adalah sebuah danau yang terletak di desa Sedoa, Lo...

Region of south-central Southern America For the Bolivian province, see Gran Chaco Province. For the Argentine province, see Chaco Province. For the region of Paraguay, see Chaco (Paraguay). This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (May 2020) Gran ChacoDry ChacoLandscape in the Gran Chaco, Chaco Boreal, ParaguayDry Chaco as delimited by the ...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

American high jumper (born 1928) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: George Stanich – news آ· newspapers آ· books آ· scholar آ· JSTOR (April 2009) (Learn how and when to remove this mess...

ط§ظ„ط¹ظ„ط§ظ‚ط§طھ ط§ظ„ط¨ظˆط³ظ†ظٹط© ط§ظ„ظپظٹط¬ظٹط© ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ ظپظٹط¬ظٹ ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ ظپظٹط¬ظٹ طھط¹ط¯ظٹظ„ ظ…طµط¯ط±ظٹ - طھط¹ط¯ظٹظ„ ط§ظ„ط¹ظ„ط§ظ‚ط§طھ ط§ظ„ط¨ظˆط³ظ†ظٹط© ط§ظ„ظپظٹط¬ظٹط© ظ‡ظٹ ط§ظ„ط¹ظ„ط§ظ‚ط§طھ ط§ظ„ط«ظ†ط§ط¦ظٹط© ط§ظ„طھظٹ طھط¬ظ…ط¹ ط¨ظٹظ† ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ ظˆظپظٹط¬ظٹ.[1][2][3][4][5] ظ…ظ‚ط§ط±ظ†ط© ط¨ظٹظ† ط§ظ„ط¨ظ„ط¯ظٹظ† ظ‡ط°ظ‡ ظ…ظ‚ط§ط±ظ†ط© ط¹ط§ظ…ط© ظˆظ…ط±ط¬ط¹ظٹط© ظ„ظ„ط¯ظˆظ„طھظٹ...
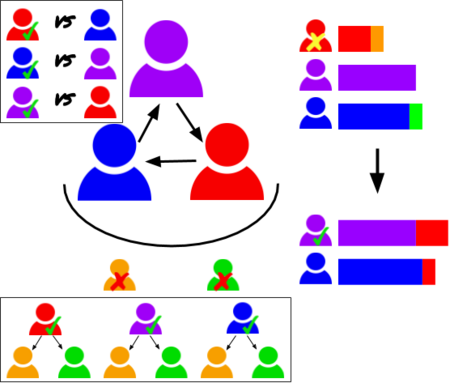
Single-winner electoral system family Part of the Politics and Economics seriesElectoral systems Comparison of electoral systemsSocial choice theoryMechanism designList (By country) Single-winner methodsSingle vote-runoff methods Plurality (FPP) Two-round (US: Jungle primary) Partisan primary Alternative vote (US: Ranked-choice) Condorcet-IRV Condorcet methods Ranked pairs Schulze Minimax Kemeny–Young Nanson Condorcet-IRV Maximal lottery Positional voting First-preference plurality Borda co...

â†گ 2012 • • 2020 → Elecciones al Parlamento de Galicia de 2016Parlamento de Galicia para la X legislatura Fecha 25 de septiembre de 2016 Tipo autonأ³micas Cargos a elegir 75 diputados que, a su vez, eligen al presidente de la Junta Demografأa electoral Votantes 1 448 962 Participaciأ³n 53.63 % 1.8 % Votos vأ،lidos 1 434 418 Votos nulos 14 544 Resultados PPdeG – Alberto Nأ؛أ±ez Feijأ³o Vo...

Prussian philosopher, government official, diplomat, and educator (1767–1835) Wilhelm von HumboldtPortrait by Thomas LawrenceBorn(1767-06-22)22 June 1767Potsdam, PrussiaDied8 April 1835(1835-04-08) (aged 67)Tegel, PrussiaEducationUniversity of Frankfurt (Oder)University of Gأ¶ttingenSpouseCaroline von Dacherأ¶denEra19th-century philosophyRegionWestern philosophySchoolBerlin Romanticism[1]Romantic linguistics[2]Classical liberalismInstitutionsUniversity of BerlinMain int...































