חוג רגולרי פון-נוימן
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Anyang – berita · surat kabar · buku · cendekiawan · JSTOR Sepiring Anyang Anyang adalah sejenis makanan tradisional dari Provinsi sumatera barat dan masyarakat Minangkabau umumnya. Masyarakat Minangkaba...

1859 painting by Francesco Hayez This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Kiss Hayez – news · newspapers · books · scholar · JSTOR (February 2020) (Learn how and when to remove this template message) The KissArtistFrancesco HayezYear1859Mediumoil on canvasDimensions110 cm × 88&...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Hitam putih – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2013) Halaman ini berisi artikel tentang istilah yang dipakai di media dan komputer. Untuk album Juliette, lihat Hitam Putih. Untuk aca...

Arkade perbelanjaan di Koenji Kōenji (高円寺code: ja is deprecated ) adalah nama kawasan di Suginami, Tokyo, sebelah barat Shinjuku. Nama kawasan ini diambil dari nama kuil Buddha di tempat ini. Koenji berada dekat dari pusat Tokyo. Khususnya daerah sekitar stasiun Koenji memakmurkan di Koenji. Demografi Koenji adalah kota yang terkenal baik untuk muda-mudi. Ada banyak pertokoan di daerah sekitar stasiun Koenji, di dalam situ ada banyak toko yang orang muda sukai. Yaitu toko baju lama, to...

The Late Late Show with James CordenGenreGelar wicaraAcara variasiSatire politikDitulis olehMike Gibbons (penulis utama)SutradaraTrollbäck + Company(judul)Tim Mancinelli (acara utama)PresenterJames CordenPemeranReggie Watts, The Late Late Show BandPenggubah lagu temaReggie WattsHagar Ben-AriGuillermo E. BrownSteve ScalfatiTim YoungLagu pembukaThe Late Late ShowNegara asalAmerika SerikatBahasa asliInggrisJmlh. musim9Jmlh. episode1.172 (per 02 Maret 2023) (daftar episode)ProduksiProduser ekse...

Marvel Comics fictional characterComics character Cal'syee NeramaniDeathbirdCal'syee Neramani / Deathbird as depicted in New Mutants vol. 4 #5(January 2020).Art by Rod Reis.Publication informationPublisherMarvel ComicsFirst appearanceMs. Marvel #9(September 1977)Created byChris Claremont (writer) Keith Pollard (penciler)In-story informationAlter egoCal'syee NeramaniSpeciesShi'ar mutantTeam affiliationsHorsemen of ApocalypseShi'ar ImperiumThe BroodStarforceNotable aliasesDeathbirdWarAbilities ...

2020 miniseries by Ethan Hawke The Good Lord BirdOfficial posterGenre Historical drama Dark comedy[1][2] Created by Ethan Hawke Mark Richard Based onThe Good Lord Birdby James McBrideStarring Ethan Hawke Hubert Point-Du Jour Beau Knapp Nick Eversman Ellar Coltrane Jack Alcott Mo Brings Plenty Daveed Diggs Joshua Caleb Johnson Opening themeCome on Children, Let's Sing by Mahalia Jackson[3]Country of originUnited StatesOriginal languageEnglishNo. of episodes7ProductionEx...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rollamienta – news · newspapers · books · scholar · JSTOR (May 2024) (Learn how and when to remove this message) Municipality in Castile and León, SpainRollamientaMunicipalityParish Church of RollamientaRollamientaLocation in Spain.Show map of Castile and Leó...

2012 video gameUFC Undisputed 3Cover art featuring former UFC Middleweight Champion Anderson The Spider Silva, who won a fan vote to appear on the cover of the game.Developer(s)Yuke'sPublisher(s)THQComposer(s)Pride FC music composed by Yasuharu TakanashiPlatform(s)PlayStation 3, Xbox 360ReleaseNA: 14 February 2012EU: 14 February 2012AU: 16 February 2012JP: 1 March 2012Genre(s)SportsMode(s)Single-player, multiplayer UFC Undisputed 3 is a mixed martial arts video game featuring Ultimate Fightin...
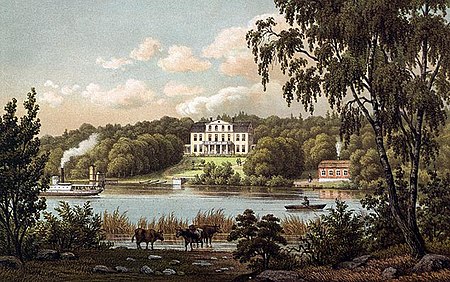
59°37′25″N 17°39′10″E / 59.62361°N 17.65278°E / 59.62361; 17.65278 Signhildsberg, 2012. Signhildsberg 1881, lithography by Alexander Nay. Building in Upplands-Bro Municipality, Stockholm County, Sweden Signhildsberg (historically Fornsigtuna, where forn means ancient, Old Sigtuna, Sithun, Signesberg) is a manor that formerly was a royal estate (Uppsala öd), located in the parish of Håtuna approximately 4 kilometres (2.5 mi) west of the modern town of...

American classical composer (1873–1954) J. Rosamond Johnson, right, with Bob Cole J. Rosamond Johnson, photo by Carl Van Vechten (1933) John Rosamond Johnson (August 11, 1873 – November 11, 1954; usually referred to as J. Rosamond Johnson)[1] was an American composer and singer during the Harlem Renaissance. Born in Jacksonville, Florida, he had much of his career in New York City. Johnson is noted as the composer of the tune for the hymn Lift Every Voice and Sing. It was first pe...

Papilio BuddhaPoster resmiSutradaraJayan K. CherianProduserPrakash BareThampy AntonyDitulis olehJayan K. CherianPemeranS. P. SreekumarSaritha KukkuDavid BriggsKallen PokkudanPadmapriyaPrakash BareThampy AntonySinematograferM J RadhakrishnanPenyuntingSujoy JosephPerusahaanproduksiSilicon MediaKayal FilmsTanggal rilis 15 Maret 2013 (2013-03-15) Durasi108 menitNegaraIndiaBahasaMalayalamInggris Papilio Buddha adalah film India tahun 2013 yang ditulis dan disutradarai oleh Jayan K. Cherian.&#...

American lyricist and songwriter (1924–2023) Sheldon HarnickHarnick in 2006Background informationBirth nameSheldon Mayer HarnickBorn(1924-04-30)April 30, 1924Chicago, Illinois, U.S.DiedJune 23, 2023(2023-06-23) (aged 99)New York City, New York, U.S.GenresMusical theaterOccupation(s)LyricistYears active1949–2023Spouse(s) Mary Boatner (m. 1950; ann. 1957) Elaine May (m. 1962; div. 1963)R...

Sports governing body Football Federation of MacedoniaUEFAShort nameFFMFounded14 August 1949; 74 years ago (1949-08-14)[1]HeadquartersSkopjeFIFA affiliation1994UEFA affiliation1994PresidentMuamed SejdiniWebsiteffm.mk The Football Federation of Macedonia (FFM; Macedonian: Фудбалска Федерација на Македонија, ФФМ) or Football Federation of North Macedonia[2][3] is the governing body of football in North Macedonia based i...

Sanskrit term for mental impressions This article is about the Hindu concept of impressions on the mind. For other uses, see Samskara (disambiguation). In Indian philosophy and some Indian religions, samskaras or sanskaras (Sanskrit: संस्कार) are mental impressions, recollections, or psychological imprints. In Hindu philosophies, samskaras are a basis for the development of karma theory.[1][2] In Buddhism, the Sanskrit term samskara is used to describe mental for...

Paolo Gioviovescovo della Chiesa cattolica Incarichi ricopertiVescovo di Nocera (1528-1552) Nato21 aprile 1483 a Como Nominato vescovo13 gennaio 1528 da papa Clemente VII Consacrato vescovo17 aprile 1533 dall'arcivescovo Gabriele Mascioli, O.E.S.A. Deceduto12 dicembre 1552 (69 anni) a Firenze Manuale Paolo Giovio (Como, 21 aprile 1483 – Firenze, 12 dicembre 1552) è stato un vescovo cattolico, storico, medico, biografo e museologo italiano. Stemma della famiglia Giov...

О фильме см. Удостоверение (фильм). Эта статья или раздел нуждается в переработке.Пожалуйста, улучшите статью в соответствии с правилами написания статей. Удостоверение Разворот служебного удостоверения Председателя КГБ СССР Юрия Андропова Выдаётся в территориал�...

玉水嘉一(左)と富松正安(右) 加波山事件(かばさんじけん)とは、1884年(明治17年)9月23日に発生した栃木県令三島通庸等の暗殺未遂事件。 概要 自由民権運動の激化事件の一つであり、急進的な考えを抱いた若き民権家たちが起こした。福島事件に関わった河野広躰(河野広中の甥)等のグループが中心で、これに茨城県・下館の富松正安や栃木県内の民権家が�...

CLCCLC tại K-pop Sharing Festival vào tháng 4 năm 2018Từ trái sang phải: Sorn, Seungyeon, Elkie, Yeeun, Eunbin, Yujin và Seunghee.Thông tin nghệ sĩTên gọi khácCrystaL ClearNguyên quánSeoul, Hàn QuốcThể loạiK-popDance-popBubblegum-popR&BBalladHip-hopPopElectronic-popNăm hoạt động2015 (2015)–2022[a] (2022[a])Công ty quản lýCube EntertainmentHãng đĩa CJ E&M (2015-2018) LOEN Entertainment (2018-2022) Hợp...

「山椒魚」はこの項目へ転送されています。井伏鱒二の小説については「山椒魚 (小説)」を、つげ義春の漫画については「山椒魚 (漫画)」をご覧ください。 「サンショウモ」とは異なります。 サンショウウオ エゾサンショウウオ Hynobius retardatus 分類 ドメイン : 真核生物 Eukaryota 界 : 動物界 Animalia 門 : 脊索動物門 Chordata 亜門 : 脊椎動物亜門 Vertebrata 綱 : 両生綱 Amphibia �...




















