המצאה
|
Read other articles:
Head of the Catholic Church from c. 99 to c. 107 Aristus redirects here. For other people with this name, see Aristus (disambiguation). Pope SaintEvaristusBishop of RomePope Evaristus, 15th centuryChurchEarly ChurchPapacy beganc. 99Papacy endedc. 107PredecessorClement ISuccessorAlexander IPersonal detailsBornBethlehem, JudeaDiedc. 107Rome, Roman EmpireSainthoodFeast day26 October Pope Evaristus (Greek: Ευάριστος) was the bishop of Rome from c. 99 to his death c. 107.[1][2...
Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...
Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...
† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...
جامع الشيخ موسى معلومات عامة القرية أو المدينة بغداد/ الكرخ الدولة العراق تاريخ بدء البناء 1119 هـ/1707م المواصفات المساحة 1000 م2 عدد المصلين 300 عدد المآذن 1 عدد القباب 1 التفاصيل التقنية المواد المستخدمة الطابوق التصميم والإنشاء النمط المعماري إسلامية قديمة المقاول الحاج أحمد ...
American comic strip For other uses, see Safe haven (disambiguation). Safe HavensSafe Havens BannerAuthor(s)Bill HolbrookWebsitewww.safehavenscomic.comCurrent status/scheduleUpdating weekdays and Saturdays, no Sunday.Launch dateOctober 3, 1988; 35 years ago (October 3, 1988)Syndicate(s)Washington Post Writers Group (1988-1992);King Features Syndicate (1993-present)Genre(s)Dramedy, satirePreceded byOn the Fastrack Safe Havens is a comic strip drawn by cartoonist Bill Holbrook. It ...
International cricket tour Indian cricket team in South Africa in 2021–22 South Africa IndiaDates 26 December 2021 – 23 January 2022Captains Dean Elgar (Tests)Temba Bavuma (ODIs) Virat Kohli[n 1] (Tests)KL Rahul (ODIs)Test seriesResult South Africa won the 3-match series 2–1Most runs Keegan Petersen (276) KL Rahul (226)Most wickets Kagiso Rabada (20) Mohammed Shami (14)Player of the series Keegan Petersen (SA)One Day International seriesResults South Africa won...
2022 single by Chris Brown featuring WizkidCall Me Every DaySingle by Chris Brown featuring Wizkidfrom the album Breezy ReleasedJune 17, 2022Recorded2021–2022GenreAfro-fusion[1]Length2:29LabelRCACBESongwriter(s)Chris BrownAyodeji BalogunThierry Augustin LohierProducer(s)Blaise BeatzDJ TunezRoccStarChris Brown singles chronology Monalisa (Remix) (2022) Call Me Every Day (2022) Under the Influence (2022) Wizkid singles chronology Mood(2022) Call Me Every Day(2022) IDK(2024) Mu...
Governor of Kentucky from 2007 to 2015 Steve BeshearBeshear in 201361st Governor of KentuckyIn officeDecember 11, 2007 – December 8, 2015Lieutenant Daniel Mongiardo Jerry Abramson Crit Luallen Preceded byErnie FletcherSucceeded byMatt Bevin49th Lieutenant Governor of KentuckyIn officeDecember 13, 1983 – December 8, 1987GovernorMartha Layne CollinsPreceded byMartha Layne CollinsSucceeded byBrereton Jones43rd Attorney General of KentuckyIn officeDecember 11, 1979 –&...
Persian saint, virgin, and martyr (d. between 341 and 349) Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (April 2024) (Learn how and when to remove this message) Saint TarbulaDied341 or 349IraqVenerated inCatholic Church, Orthodox ChurchFeast4 April Tarbula (d. between 341 and 349), also called Tarbu, Therbuta, Pherbutha, and Phermoutha,[1 ...
O'Byrne. The O'Byrne family (Irish: Ó Broin) is an Irish clann that descend from Bran mac Máelmórda, King of Leinster, of the Uí Faelain of the Uí Dúnlainge. Before the Norman invasion of Ireland they began to colonise south Wicklow. There are many famous people with this Irish last name. This includes Anna O’Byrne, an Australian singer and actress, and Anna Marie O’Byrne, an American model. Map of southeast Leinster in the 16th century; O'Byrne territory is labelled Críoch Branac...
1875-1877 U.S. Congress 44th United States Congress43rd ←→ 45thUnited States Capitol (1877)March 4, 1875 – March 4, 1877Members76 senators293 representatives9 non-voting delegatesSenate majorityRepublicanSenate PresidentHenry Wilson (R) (until November 22, 1875) Vacant (from November 22, 1875)House majorityDemocraticHouse SpeakerMichael C. Kerr (D) until August 19, 1876 Samuel J. Randall (D) from December 4, 1876SessionsSpecial: March 5, 1875 – March 24, 18751st: December 6,...
Argumentation for the sake of winning the argument instead of reaching or seeking truth Part of a series onRhetoric History Ancient Greece Asianism Atticism Attic orators Calliope Sophists Ancient India Ancient Rome The age of Cicero Second Sophistic Middle Ages Byzantine rhetoric Trivium Renaissance Studia humanitatis Modern period Concepts Captatio benevolentiae Chironomia Decorum Delectare Docere Device Eloquence Eloquentia perfecta Eunoia Enthymeme Facilitas Fallacy Informal Figure of spe...
此條目需要擴充。 (2008年9月16日)请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 阿德南·门德列斯Adnan Menderes第9任土耳其總理任期1950年5月22日—1960年5月27日总统傑拉勒·拜亞爾前任塞姆斯丁·居纳尔塔伊继任傑馬勒·古爾塞勒土耳其民主党领袖任期1950年6月9日—1960年5月27日前任傑拉勒·拜亞爾继任职位废除Template:GNAT ...
دوري السوبر الأوغندي 2006 تفاصيل الموسم الدوري الأوغندي الممتاز البلد أوغندا المنظم اتحاد أوغندا لكرة القدم البطل نادي سلطة أوغندا للدخل عدد المشاركين 15 دوري السوبر الأوغندي 2005 دوري السوبر الأوغندي 2006-07 تعديل مصدري - تعديل دوري السوبر الأوغندي 200...
Filipino lawyer and politician (1859-1941) In this Spanish name, the first or paternal surname is Agoncillo and the second or maternal family name is Encarnación. DonFelipe Agoncillo y EncarnaciónA portrait of Don Felipe AgoncilloSecretary of InteriorIn office1923–1925Appointed byLeonard WoodPreceded byJose P. LaurelSucceeded byHonorio VenturaMember of the Philippine Assembly from Batangas's 1st districtIn office1907–1909Preceded byPost establishedSucceeded byGalicano Apacible P...
Play, film, or television programme with only two main characters Not to be confused with Two-handed (disambiguation). This article may contain excessive or irrelevant examples. Please help improve the article by adding descriptive text and removing less pertinent examples. (September 2018) The two characters Ben and Gus in Harold Pinter's The Dumb Waiter A two-hander is a term for a play, film, or television programme with only two main characters.[1] The two characters in question o...
Meißen rural district of Saxony (en) Option municipality (en) Tempat Negara berdaulatJermanNegara bagian di JermanSaxonia NegaraJerman Ibu kotaMeißen Pembagian administratifCoswig Diera-Zehren Ebersbach (en) Glaubitz (en) Gröditz Großenhain Hirschstein (en) Käbschütztal Klipphausen Lampertswalde Lommatzsch Meißen Moritzburg (en) Niederau (en) Nossen Nünchritz (en) Priestewitz (en) Radebeul (en) Radeburg Riesa (en) Röderaue Schönfeld (en) Stauchitz (en) Strehla (en) Thiendorf Weinbö...
British philosopher Ray BrassierBornRaymond Brassier1965 (age 58–59)London, EnglandNationalityBritishAlma materUniversity of North LondonUniversity of WarwickEraContemporary philosophyRegionWestern philosophySchoolContinental philosophySpeculative realism (transcendental nihilism)InstitutionsMiddlesex UniversityAmerican University of BeirutMain interestsNihilism, realism, materialism, methodological naturalism, antihumanism, MarxismNotable ideasTranscendental nihilism, philoso...
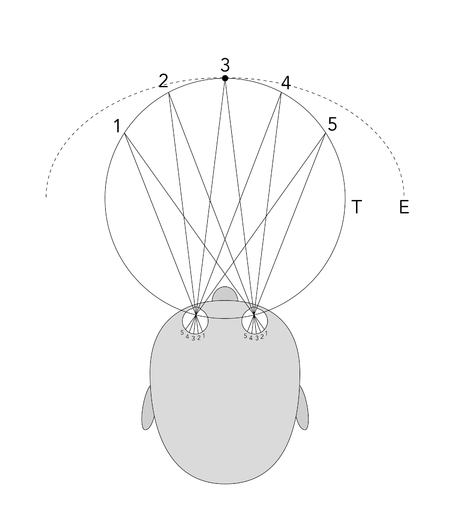
All points in space which project onto the same points in the retinas of both eyes Schematic representation of the theoretical (T) and the empirical (E) horopter. In vision science, the horopter was originally defined in geometric terms as the locus of points in space that make the same angle at each eye with the fixation point, although more recently in studies of binocular vision it is taken to be the locus of points in space that have the same disparity as fixation. This can be defined the...