הוכחת האי-מנייה הראשונה של קנטור
|
Read other articles:

La parola greca ἄθεοι (atheoi, [coloro che sono] senza dio) come compare nella lettera agli Efesini 2,12[1][2] tramandata dal Papiro 46 (inizio del III secolo). Questo termine è assente nel resto del Nuovo Testamento, e nella versione greca della Bibbia ebraica. L'ateismo (in greco antico: ἄθεος?, àtheos, composto da α- privativo, senza, e θεός, dio, letteralmente senza dio) è la posizione di chi non crede nell'esistenza di Dio[3][4][...

Gijsbert Hendrik Lamers Gijsbert Hendrik Lamers (15 Desember 1834 – 11 Juni 1905) adalah seorang teolog Reformed asal Belanda. Gijsbert Hendrik lahir dari pasangan pendeta Sohn des Pfarrers Gijsbert Lamers (lahir pada 24 Juli 1791 di Arnhem - wafat pada 20 Mei 1869 di Harderwijk) dan Frau Jeannetta Brans Buddingh (lahir sekitar tahun 1798 di Elst - wafat pada 9 Januari 1866 di Harderwijk). Ia juga merupakan paman dari Albertus Christiaan Kruyt, seorang misionaris Belanda dan m...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Revolusi tahun 1848 di negara-negara ItaliaBagian dari Peperangan Penyatuan ItaliaPara prajurit Italia mempertahankan Venesia melawan pasukan AustriaTanggal1848LokasiItaliaHasil Revolusi gagal; beberapa pemberontak menyatakan konstitusi liberal, namun mereka semua kemudian dibubarkanPerubahanwilayah Tidak adaPihak terlibat Kerajaan Sisilia Pemerintahan Sementara Milan Republik San Marco Republik RomaDidukung oleh: Kerajaan Sardinia Kekaisaran Austria Kerajaan Dua Sisilia Negara GerejaTokoh da...

Medical conditionInterstitial cystitisOther namesBladder pain syndrome (BPS),[1] painful bladder syndrome (PBS), IC/BPS, IC/PBS, UCPPS[2]Hunner's lesion seen in some interstitial cystitis patients by cystoscopy[3][4]Pronunciation/ˌɪntərˈstɪʃəl sɪˈstaɪtɪs/ IN-tər-STISH-əl sist-EYE-tis SpecialtyUrologySymptomsChronic pain of the bladder, feeling the need to urinate right away, needing to urinate often, pain with sex[1]ComplicationsDepre...

Pedestrian tunnel and underground shopping centre in Ontario, Canada This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Path Toronto – news · newspapers · books · scholar · JSTOR (October 2018) (Learn how and when to remove this template message) PathPath network viewed from under Commerce CourtLocationTor...

Indian politician (1897–1990) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Prafulla Chandra Sen – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this template message) Prafulla Chandra Sen2nd Chief Minister of West BengalIn office2 July 1962 – 28 Fe...

National Educational TelevisionLogo National Educational Television.JenisJaringan televisi berlangganan terestrial gratisNegaraAmerika SerikatDidirikan21 November 1952 Washington, D.C., Amerika SerikatMarkasKota New YorkWilayah siarAmerika Serikat dan KanadaPemilikFord Foundation (1954–1970)Corporation for Public Broadcasting (1967–1970)Tanggal luncur16 Mei 1954Ditutup4 Oktober 1970 National Educational Television (disingkat NET) adalah jaringan televisi Amerika Serikat yang dimiliki oleh...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Pier Antonio Torroni Nazionalità Italia Altezza 179 cm Peso 66 kg Calcio Ruolo Difensore Termine carriera 1999 CarrieraSquadre di club1 1979-1981 Forlimpopoli40 (0)1981-1988 Modena193 (3)1988-1990 Perugia65 (0)1990-1992 Spezia64 (0)1992-1993 Massese29 (0)1993-1994 Mantova2...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Ramon Magsaysay AwardNegaraFilipinaDipersembahkan olehRamon Magsaysay Award FoundationDiberikan perdana1957Situs webhttp://www.rmaf.org.ph Ramon Magsaysay Award atau Hadiah Ram...

German footballer (1929–2003) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Helmut Rahn – news · newspapers · books · scholar · JSTOR (March 2021) (Learn how and when to remove this message) Helmut Rahn Rahn in 1962Personal informationDate of birth (1929-08-16)16 August 1929Place of birth Essen, GermanyD...

Professional wrestling women's championship World of Stardom ChampionshipThe current design of the title (2020–present)DetailsPromotionWorld Wonder Ring StardomDate establishedJune 26, 2011[1]Current champion(s)MaikaDate wonDecember 29, 2023StatisticsFirst champion(s)Nanae Takahashi[1]Most reignsIo Shirai and Mayu Iwatani(2 reigns)Longest reignNanae Takahashi(602 days)Shortest reignAlpha Female(43 days)Oldest championMeiko Satomura(35 years, 251 days)Youngest championYoshiko...

Hungarian footballer András Telek Telek András in 2011.Personal informationDate of birth (1970-12-10) 10 December 1970 (age 53)Place of birth BudapestPosition(s) DefenderYouth career–1989 Ferencvárosi TCSenior career*Years Team Apps (Gls)1989–1996 Ferencvárosi TC 1997–1998 1. FC Košice 1998–1999 Ferencvárosi TC 1999 Dunakeszi VSE 2000 Jilin Aodong 2001–2002 Zalaegerszegi TE International career1992–1996 Hungary 24 (0)Managerial career2005–2006 Hungary (women) *Club do...

Indian breed of goat SirohiSpotted Sirohi billiesConservation statusFAO (2007): not at risk[1]: 59 DAD-IS (2021): not at risk[2]Country of originIndiaDistributionRajasthanGujaratUsemeat, milkTraitsWeightMale: 50 kg[2]Female: 23 kg[2]HeightMale: 86 cm[2]Female: 68 cm[2]Horn statussmall back-curved horns in both sexesTasselsusually presentGoatCapra hircus The Sirohi is an Indian breed of domestic goat. It is named for its area of o...
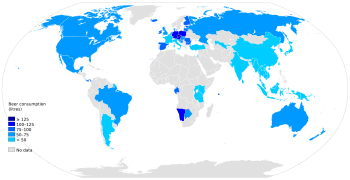
Not to be confused with Dipsomania. This article needs more reliable medical references for verification or relies too heavily on primary sources. Please review the contents of the article and add the appropriate references if you can. Unsourced or poorly sourced material may be challenged and removed. Find sources: Potomania – news · newspapers · books · scholar · JSTOR (September 2020) Medical conditionPotomaniaOther namesBeer potomania, Beer drinker...

2012 studio album by Stevie StoneRollin' StoneStudio album by Stevie StoneReleasedJune 12, 2012Recorded2011–2012GenreHip hopLength52:35LabelStrange MusicProducer40 oz., Aaron Naeger, Ben Cybulsky, Frizz, Johnny Juliano, Koko, Nardo, Rip Knoxx, Seven, Rell, Tali Blanco, Oliver Grose aka OGtha3, Tom, Wyshmaster, WLPWRStevie Stone chronology New Kid Comin(2009) Rollin' Stone(2012) Momentum(2012) Rollin' Stone is the second studio album by American rapper Stevie Stone. The album was rel...

UFC 200: Tate vs. NunesProdotto daUltimate Fighting Championship Data9 luglio 2016 Città Las Vegas, Stati Uniti SedeT-Mobile Arena Spettatori18.202 Cronologia pay-per-viewThe Ultimate Fighter 23 FinaleUFC 200: Tate vs. NunesUFC Fight Night: McDonald vs. Lineker Progetto Wrestling Manuale UFC 200: Tate vs. Nunes è stato un evento di arti marziali miste tenuto dalla Ultimate Fighting Championship svolto il 9 luglio 2016 alla T-Mobile Arena di Las Vegas, Stati Uniti.[1] Indice 1 Retros...

Christine BaranskiLahirChristine Jane BaranskiPekerjaanAktrisSuami/istriMatthew Cowles (1983-sekarang)PenghargaanCritics Choice Award for Best Cast2002 Chicago Penghargaan(2002) Screen Actors Guild Award for Outstanding Performance by a Cast in a Motion Picture (en) (1996) Screen Actors Guild Award for Outstanding Performance by a Female Actor in a Comedy Series (en) (1996) Screen Actors Guild Award for Outstanding Performance by a Cast in a Motion Picture (en) (1995) Primetime Emmy Award fo...

Eurovision Song Contest 2016Country ItalyNational selectionSelection processSanremo Music Festival 2016Selection date(s)Artist: 14 February 2016 Song: 14 March 2016Selected entrantFrancesca MichielinSelected songNo Degree of SeparationSelected songwriter(s)Federica AbbateFrancesca MichielinCheopeFabio GargiuloNorma Jean MartineFinals performanceFinal result16th, 124 pointsItaly in the Eurovision Song Contest ◄2015 • 2016 • 2017► Italy participated i...


![{\displaystyle \ [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c40bbeaa2f59e60b6259cebe2479bc24396f0)


















