Ч”Ч”ЧЎЧӣЧқ Ч”Ч’'Ч ЧҳЧңЧһЧ Чҷ (1907)
|
Read other articles:

Ancient Egyptian personification of primordial darkness This article is about a concept in ancient Egyptian mythology. For other uses, see Kek (disambiguation). KekKauket (left) and Kek (right) sitting on thrones, relief from a temple at Deir el-MedinaName in hieroglyphs Kek Kekui Kekuit Major cult centerHermopolis (as a member of the Ogdoad)Personal informationSpouseKauket Kek is the deification of the concept of primordial darkness[1] in the ancient Egyptian Ogdoad cosmogony of Herm...

Kenwa MabuniLahir(1889-11-14)14 November 1889Shuri, OkinawaMeninggal23 Mei 1952(1952-05-23) (umur 62)Tokyo, JepangGayaShitЕҚ-ryЕ«GuruAnkЕҚ Itosu, Higaonna KanryЕҚPeringkatPendiri ShitЕҚ-ryЕ«Siswa TerkemukaKenei Mabuni, Iwata Manzo, ChЕҚjirЕҚ Tani Kenwa Mabuni (ж‘©ж–Үд»Ғ иіўе’Ңcode: ja is deprecated , Mabuni Kenwa, 14 November 1889 - 23 Mei 1952) adalah salah satu karateka pertama yang mengajarkan karate di daratan utama Jepang dan dikenal karena mengembangkan sebuah gaya yang dikenal seb...

Pour les articles homonymes, voir Mezzana. Cet article est une Г©bauche concernant une localitГ© italienne et le Trentin-Haut-Adige. Vous pouvez partager vos connaissances en lвҖҷamГ©liorant (comment ?) selon les recommandations des projets correspondants. Mezzana Administration Pays Italie RГ©gion Trentin-Haut-Adige Province Trentin Code postal 38020 Code ISTAT 022114 Code cadastral F168 PrГ©fixe tel. 0463 DГ©mographie Population 880 hab. (1er janvier 2023[1]) DensitпҝҪ...

жӯӨжўқзӣ®д»Ӣзҙ№зҡ„жҳҜжӢүдёҒеӯ—жҜҚдёӯзҡ„第2дёӘеӯ—жҜҚгҖӮе…ідәҺе…¶д»–з”Ёжі•пјҢиҜ·и§ҒгҖҢB (ж¶Ҳжӯ§д№ү)гҖҚгҖӮ жҸҗзӨәпјҡжӯӨжқЎзӣ®йЎөзҡ„дё»йўҳдёҚжҳҜеёҢи…Ҡеӯ—жҜҚО’гҖҒиҘҝйҮҢе°”еӯ—жҜҚР’гҖҒР‘гҖҒРӘгҖҒР¬жҲ–еҫ·иҜӯеӯ—жҜҚбәһгҖҒГҹгҖӮ BB b(и§ҒдёӢ)з”Ёжі•жӣёеҜ«зі»зөұжӢүдёҒеӯ—жҜҚиӢұж–Үеӯ—жҜҚISOеҹәжң¬жӢүдёҒеӯ—жҜҚпјҲиӢұиҜӯпјҡISO basic Latin alphabetпјүзұ»еһӢе…Ёйҹізҙ ж–Үеӯ—зӣёе…іжүҖеұһиӘһиЁҖжӢүдёҒиҜӯиҜ»йҹіж–№жі• [b][p][Й“](йҖӮеә”еҸҳдҪ“)Unicodeзј–з ҒU+0042, U+0062еӯ—жҜҚйЎәдҪҚ2ж•°еҖј 2жӯ·еҸІзҷј...

Indigenous tribe in the United States For other uses, see Tawakoni (disambiguation). TawakoniDave, a Tawakoni man, 1872Total populationfewer than 2,953[1] (2018)Regions with significant populations Oklahoma, historically Kansas and TexasLanguagesEnglish, formerly WichitaReligionNative American Church, Christianity,indigenous religionRelated ethnic groupsCaddo, Pawnee, other Wichita and Affiliated Tribes The Tawakoni (also Tahuacano and Tehuacana) are a Southern Plains...

Six U.S. Army enlisted men courts-martialed for refusing orders to Vietnam in June 1970 The Fort Lewis Six arrested in June 1970 for refusing orders to Vietnam. The Fort Lewis Six were six U.S. Army enlisted men at the Fort Lewis Army base in the Seattle and Tacoma, Washington area who in June 1970 refused orders to the Vietnam War and were then courts-martialed.[1] They had all applied for conscientious objector status and been turned down by the Pentagon. The Army then ordered them ...
е‘Ёиҷ•йҷӨдёүе®іThe Pig, The Snake and The PigeonжӯЈејҸзүҲжө·е ұеҹәжң¬иө„ж–ҷеҜјжј”й»ғзІҫз”«зӣ‘еҲ¶жқҺзғҲй»ғжұҹиұҗеӢ•дҪңжҢҮе°ҺжҙӘжҳ°йЎҘзј–еү§й»ғзІҫз”«дё»жј”йҳ®з¶“еӨ©иўҒеҜҢиҸҜйҷід»Ҙж–ҮзҺӢж·ЁжқҺжқҺд»Ғи¬қз“Ҡз…–й…Қд№җзӣ§еҫӢйҠҳжһ—еӯқиҰӘжһ—жҖқеҰӨдҝқеҚңж‘„еҪұзҺӢйҮ‘еҹҺеүӘиҫ‘й»ғзІҫз”«жһ—йӣҚзӣҠеҲ¶зүҮе•ҶдёҖзЁ®ж…ӢеәҰйӣ»еҪұиӮЎд»Ҫжңүйҷҗе…¬еҸёзүҮй•ҝ134еҲҶйҗҳдә§ең° иҮәзҒЈиҜӯиЁҖеңӢиӘһзІөиӘһеҸ°иӘһдёҠжҳ еҸҠеҸ‘иЎҢдёҠжҳ ж—Ҙжңҹ 2023е№ҙ10жңҲ6ж—Ҙ (2023-10-06)пјҲеҸ°зҒЈпјү 2023е№ҙ11жңҲ2ж—Ҙ (2023-11-02)пјҲйҰҷпҝҪ...

Austrian paramilitary organization (1923вҖ“1936) Republican Protection LeagueRepublikanischer SchutzbundEmblem of the SchutzbundFoundersSocial Democratic Party of AustriaFoundation1923Dissolved1934HeadquartersViennaActive regionsAustriaIdeologySocial democracyDemocratic socialismRepublicanismAnti-fascismAnti-monarchismAnti-clericalismFactions:Communism[1]Political positionLeft-wingFactions:Far-leftStatusDefunctSize100,000 (peak in 1925)[2]Opponents Fatherland Front O...

Palma CampaniaKomuneComune di Palma CampaniaLokasi Palma Campania di Provinsi NapoliNegaraItaliaWilayah CampaniaProvinsiNapoli (NA)Luas[1] вҖў Total20,67 km2 (7,98 sq mi)Ketinggian[2]85 m (279 ft)Populasi (2016)[3] вҖў Total14.905 вҖў Kepadatan720/km2 (1,900/sq mi)Zona waktuUTC+1 (CET) вҖў Musim panas (DST)UTC+2 (CEST)Kode pos80036Kode area telepon081Situs webhttp://www.comune.palmacampania.na.i...
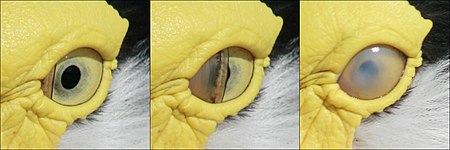
El parpadeo de los ojos de un Vanellus miles en Cairns, Queensland, Australia. La membrana nictitante se cierra de un solo lado, y es transparente. Los propios pГЎrpados no se cierran durante el parpadeo, pero lo hacen para dormir. La membrana nictitante (del latГӯn nictare, parpadear), o tercer pГЎrpado, es una caracterГӯstica fisiolГіgica propia de ciertos animales; se trata de una telilla o pГЎrpado accesorio transparente o translГәcido que puede cerrarse para proteger al globo ocular y pa...

Ethnic group of Niger Delta, Nigeria This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Urhobo people вҖ“ news В· newspapers В· books В· scholar В· JSTOR (April 201...

District of Portugal District in Norte, PortugalBraganГ§aDistrict FlagCoat of armsThe location of the District of BraganГ§a within continental PortugalCountryPortugalRegionNorteSubregionAlto TrГЎs-os-MontesHistorical ProvinceTrГЎs-os-Montes e Alto DouroDistrictBraganГ§aMunicipalitiesAlfГўndega da FГ©, BraganГ§a, Carrazeda de AnsiГЈes, Freixo de Espada Г Cinta, Macedo de Cavaleiros, Miranda do Douro, Mirandela, Mogadouro, Moncorvo, Vila Flor, Vimioso, VinhaisGovernment вҖў Civil Gov...

жҸҗзӨәпјҡжӯӨжқЎзӣ®йЎөзҡ„дё»йўҳдёҚжҳҜиҗ§гҖӮ з°«зҗҙз°«иҲҮжҙһз°«жңЁз®ЎжЁӮеҷЁжЁӮеҷЁеҲҘеҗҚиұҺеҗ№гҖҒиұҺзҜҙгҖҒйҖҡжҙһеҲҶйЎһз®ЎжЁӮеҷЁзӣёй—ңжЁӮеҷЁ е°әе…« дёңжұүж—¶жңҹзҡ„йҷ¶еҲ¶з®«еҘҸиҖ…дәәеғҸпјҢеҮәеңҹж–јеҪӯеұұжұҹеҸЈжұүеҙ–еў“пјҢи—Ҹж–јеҚ—дә¬еҚҡзү©йҷў з®«еҸҲзЁұжҙһз°«гҖҒз°«з®ЎпјҢжҳҜдёӯеңӢеҸӨиҖҒзҡ„еҗ№з®ЎжЁӮеҷЁпјҢзү№еҫөзӮәе–®з®ЎгҖҒиұҺеҗ№гҖҒй–Ӣз®ЎгҖҒйӮҠзЁңйҹізҷјиҒІ[1]гҖӮгҖҢз°«гҖҚеӯ—еңЁе”җд»Јд»ҘеүҚжң¬жҢҮжҺ’з°«пјҢе”җе®Ӣд»ҘдҫҶпјҢз”ұж–је–®з®ЎиұҺеҗ№зҡ„з°«ж—ҘжјёжөҒиЎҢпјҢдҫҝзЁұз·Ёз®Ўз°«зҲІжҺ’з°«пҝҪ...

County in Washington, United States County in WashingtonCowlitz CountyCountyCowlitz County CourthouseLocation within the U.S. state of WashingtonWashington's location within the U.S.Coordinates: 46В°11вҖІN 122В°41вҖІW / 46.19В°N 122.68В°W / 46.19; -122.68Country United StatesState WashingtonFoundedApril 21, 1854SeatKelsoLargest cityLongviewArea вҖў Total1,166 sq mi (3,020 km2) вҖў Land1,140 sq mi (3,000 km2)&#...

French actress (1921вҖ“1950) Corinne LuchaireLuchaire in 1943BornRosita Christiane Yvette Luchaire(1921-02-11)11 February 1921Paris, FranceDied22 January 1950(1950-01-22) (aged 28)Paris, FranceYears active1935вҖ“1940[1]SpouseGuy de Voisins-LaverniГЁreParentJean Luchaire (father) Corinne Luchaire (11 February 1921 вҖ“ 22 January 1950) was a French film actress who was a star of French cinema on the eve of World War II.[2] Her association with the German occupation led...

Italian actress (born 1931) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Adriana Asti вҖ“ news В· newspapers В· books В· scholar В· JSTOR (October 2023) (Learn how and when to remove this message) ...

Fairy tale For the 2002 novel, see The Frog Princess (novel). Not to be confused with The Frog Prince. The Frog PrincessThe Frog Tsarevna, Viktor Vasnetsov, 1918Folk taleNameThe Frog PrincessAarneвҖ“Thompson groupingATU 402 (The Animal Bride)RegionEastern EuropePublished inRussian Fairy Tales by Alexander AfanasyevRelated Puddocky The Three Feathers The Frog Princess is a fairy tale that has multiple versions with various origins. It is classified as type 402, the animal bride, in the AarneпҝҪ...

Indian Odia-language TV news channel Television channel News18 OdiaCountryIndiaBroadcast areaIndiaHeadquartersBhubaneswar, Odisha, IndiaProgrammingLanguage(s)OdiaPicture format4:3 (576i, SDTV)OwnershipOwnerTV18Sister channelsNews18 IndiaCNN-News18News18 BanglaNews18 LokmatNews18 GujaratiNews18 KannadaNews18 Tamil NaduNews 18 KeralaNews18 J&K-Ladakh-HimachalNews18 Assam North EastNews18 Uttar Pradesh UttarakhandNews18 Madhya Pradesh-ChhattisgarhNews18 Bihar-JharkhandNews18 Punjab-HaryanaNe...

Mountain pass in British Columbia, Canada Coquihalla SummitSouthern approach to Coquihalla Summit as viewed from Yak PeakElevation1,244 m (4,081 ft)Traversed by Highway 5 (Coquihalla Highway)LocationBritish Columbia, CanadaRangeNorth CascadesCoordinates49В°35вҖІ50.3вҖіN 121В°04вҖІ41.3вҖіW / 49.597306В°N 121.078139В°W / 49.597306; -121.078139Topo mapNTS 92H11 Spuzzum Coquihalla Summit (el. 1,244 m or 4,081 ft) is a highway summit along the Coquihalla High...

Tensor describing energy momentum density in spacetime Contravariant components of the stressвҖ“energy tensor. General relativity G μ ν + Λ g μ ν = κ T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }} Introduction HistoryTimelineTests Mathematical formulation Fundamental concepts Equivalence principle Special relativity World line Pseudo-Riemannian manifold Phenomena Kepler problem Gravitational lensing Gravita...