![]() ОъОбОеОЏОф ОЉОДОеОф ОЕОЎОЋОў ОћОЎОљ ОъОбОеОЏОф ОаОцОЋОдОћ ОЋОъОЋОЏОеОф ОЉОфОЌОЋОЮ ОћОеОЏОЉ, ОћОъОЉОЋОАОАОф ОбОю ОЉОДОе PID[1] ОюОЕОЮ ОЕОюОЎОўОћ ОбОю ОъОћОЎОеОЋОф ОЏОюОЎ ОеОЏОЉ ОЉОфОаОљОЎ ОЊОеОџ ОъОЕОфОаОЎОЮ.
ОъОбОеОЏОф ОЉОДОеОф ОЕОЎОЋОў ОћОЎОљ ОъОбОеОЏОф ОаОцОЋОдОћ ОЋОъОЋОЏОеОф ОЉОфОЌОЋОЮ ОћОеОЏОЉ, ОћОъОЉОЋОАОАОф ОбОю ОЉОДОе PID[1] ОюОЕОЮ ОЕОюОЎОўОћ ОбОю ОъОћОЎОеОЋОф ОЏОюОЎ ОеОЏОЉ ОЉОфОаОљОЎ ОЊОеОџ ОъОЕОфОаОЎОЮ.
ОЉОДОе PID ОљОЋ ОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ-ОљОЎОаОўОњОеОюОЎ-ОЊОЎОцОеОаОдОЎОљОюОЎ (ОЉОљОаОњОюОЎОф: PID controller or three-term controller or proportionalРђЊintegralРђЊderivative controller) ОћОЋОљ ОъОаОњОаОЋОЪ ОъОЕОЋОЉ ОбОЉОЋОе ОЌОЋОњОЎ ОЉОДОеОћ, ОћОаОъОдОљ ОЉОЕОЎОъОЋОЕ ОаОеОЌОЉ ОЉОъОбОеОЏОЋОф ОЉОДОеОћ ОфОбОЕОЎОЎОфОЎОЋОф, ОЋОЉОъОњОЋОЋОЪ ОњОЊОЋОю ОЕОю ОъОбОеОЏОЋОф ОЉОДОеОћ ОљОЌОеОЋОф. ОфОцОЋОдОфОЋ ОћОеОЌОЉОћ ОЕОю ОћОЉОДОе ОаОЋОЉОбОф ОъОћОЎОЋОфОЋ ОЉОДОе ОЉОбОю ОцОбОЋОюОћ ОъОфОъОўОЎОф ОцОЕОЋОўОћ ОюОћОЉОаОћ ОЋОДОюОћ ОюОћОўОъОбОћ ОЉОъОбОеОЏОЋОф ОцОЎОќОЎОДОюОЎОЋОф ОеОЉОЋОф, ОЏОџ ОЕОњОЮ ОъОЕОфОъОЕ ОЕОљОЎОаОЋ ОЉОбОю ОћОЉОаОћ ОбОъОЋОДОћ ОЉОфОЎОљОЋОеОЎОћ ОћОбОЋОъОЊОф ОъОљОЌОЋОеОЎОЋ ОЎОЋОЏОю ОюОЉОдОб ОЉОЋ ОЕОЎОъОЋОЕ ОЋОюОћОфОљОЎОЮ ОљОЋОфОЋ ОюОъОўОеОЋОфОЎОЋ, ОЋОъОЏОџ ОЕОќОћОЋ ОћОЉОДОе ОћОцОЕОЋОў ОЉОЎОЋОфОе ОћОюОЋОДОЌ ОЉОЌОЕОЉОЋОЪ ОљОф ОбОеОЏОЎ ОћОЕОњОЎОљОћ ОЉОбОЉОе, ОЉОћОЋОЋОћ ОЋОЉОбОфОЎОЊ, ОЊОЉОе ОћОъОАОцОД ОЉОДОеОћ ОўОЋОЉОћ ОћОъОАОцОЎОДОћ ОюОъОбОеОЏОЋОф ОцОЎОќОЎОДОюОЎОЋОф ОеОЉОЋОф[2]. ОћОЉОДОе ОъОДОЉОю ОЏОЏОаОЎОАОћ ОљОф ОљОЋОф ОћОЕОњОЎОљОћ  , ОћОъОЌОЋОЕОЉ ОЏОћОцОеОЕ ОЕОЉОЎОЪ ОљОЋОф ОЎОЎОЌОЋОА ОеОдОЋОЎ (ОћОбОеОџ ОљОюОЎОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОЕОћОъОбОеОЏОф ОфОњОЎОб) ОЋОъОЕОфОаОћ ОфОћОюОЎОџ (ОћОбОеОџ ОћОъОфОДОЉОю ОъОћОфОћОюОЎОџ ОЉОцОЋОбОю), ОЋОъОЋОдОЎОљ ОцОДОЋОЊОћ ОюОљОЌОе ОћОцОбОюОф ОфОЎОДОЋОЪ ОћОъОЉОЋОАОА ОбОю ОЕОюОЋОЕОћ ОеОЏОЎОЉОЎОЮ РђЊ ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ (P), ОљОЎОаОўОњОеОюОЎ (I) ОЋОЊОЎОцОеОаОдОЎОљОюОЎ (D), ОЋОъОЏОљОЪ ОЕОъОЋ.
, ОћОъОЌОЋОЕОЉ ОЏОћОцОеОЕ ОЕОЉОЎОЪ ОљОЋОф ОЎОЎОЌОЋОА ОеОдОЋОЎ (ОћОбОеОџ ОљОюОЎОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОЕОћОъОбОеОЏОф ОфОњОЎОб) ОЋОъОЕОфОаОћ ОфОћОюОЎОџ (ОћОбОеОџ ОћОъОфОДОЉОю ОъОћОфОћОюОЎОџ ОЉОцОЋОбОю), ОЋОъОЋОдОЎОљ ОцОДОЋОЊОћ ОюОљОЌОе ОћОцОбОюОф ОфОЎОДОЋОЪ ОћОъОЉОЋОАОА ОбОю ОЕОюОЋОЕОћ ОеОЏОЎОЉОЎОЮ РђЊ ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ (P), ОљОЎОаОўОњОеОюОЎ (I) ОЋОЊОЎОцОеОаОдОЎОљОюОЎ (D), ОЋОъОЏОљОЪ ОЕОъОЋ.
ОъОЉОЌОЎОаОћ ОъОбОЕОЎОф, ОЏОю ОљОЌОЊ ОъОеОЏОЎОЉОЎ ОћОЉОДОе ОъОЉОдОб ОцОбОЋОюОћ ОъОфОъОўОЎОф ОљОЌОеОф ОбОю ОљОЋОф ОћОЕОњОЎОљОћ, ОЏОљОЕОе ОъОЎОЊОф ОћОЕОцОбОфОЪ ОЕОю ОЏОю ОљОЌОф ОъОћОцОбОЋОюОЋОф ОаОДОЉОб ОбОю ОЎОЊОЎ ОъОфОЏОаОЪ ОћОЉОДОе ОЉОћОфОљОЮ ОюОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф (ОцОбОЋОюОћ ОћОъОЏОЋОаОћ "ОЏо┤о╝ОЋОЋОаОЋо╝ОЪ ОћОЉОДОе"). ОЉОЕОю ОЕОЎОДОЋОюОЎОЮ ОЏОъОЋ ОДОюОЋОф ОћОўОъОбОћ, ОаОЋОЌОЋОф ОЕОЎОъОЋОЕ ОЋОЉОЊОЎОДОћ ОЋОцОЕОўОЋОф ОћОъОбОеОЏОф, ОцОбОъОЎОЮ ОеОЉОЋОф ОаОбОЕОћ ОЕОЎОъОЋОЕ ОеОД ОЉОЌОюОД ОъОеОЏОЎОЉОЎ ОћОЉОДОе. ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОЋОћОљОЎОаОўОњОеОюОЎ ОЌОЎОЋОаОЎОЎОЮ ОюОеОЋОЉ ОЌОЋОњОЎ ОћОЉОДОеОћ, ОЋОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОъОЕОъОбОЋОфОЎ ОъОљОЋОЊ ОбОЉОЋОе ОъОбОеОЏОЋОф ОюОЉОДОеОф ОфОаОЋОбОћ (motion control)[3]. ОЉОъОДОеОћ ОЕОю ОЕОЎОъОЋОЕ ОЌОюОДОЎ ОЕОЏОќОћ ОЎОЎОДОеОљ ОћОЉОДОе ОцОбОъОЎОЮ ОеОЉОЋОф ОбОю ОЕОЮ ОћОЌОюОДОЎОЮ ОЉОћОЮ ОаОбОЕОћ ОЕОЎОъОЋОЕ ОЉОюОЉОЊ, ОЏОњОЋОЪ "ОЉОДОе PI" ОбОЉОЋОе ОЉОДОе ОћОъОЕОфОъОЕ ОЉОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОЋОћОљОЎОаОўОњОеОюОЎ ОЉОюОЉОЊ.
ОћОљОаОюОЎОќОћ ОћОфОљОЋОеОўОЎОф, ОЋОЏОЪ ОћОЕОЎОъОЋОЕ ОћОеОљОЕОЋОЪ, ОаОбОЕОЋ ОЉОфОЌОЋОЮ ОћОћОЎОњОЋОЎ ОћОљОЋОўОЋОъОўОЎ ОюОАОцОЎОаОЋОф, ОЋОцОЋОфОЌОЋ ОћОЌОю ОъОЕОаОЋОф ОћОбОЕОеОЎОЮ ОЕОю ОћОъОљОћ Оћ-20. ОюОљОЌОе ОъОЏОЪ ОаОбОЕОћ ОЉОћОЮ ОЕОЎОъОЋОЕ ОюОўОЋОЉОф ОЉОДОеОф ОфОћОюОЎОЏОЎОЮ ОљОЋОўОЋОъОўОЎОф ОЉОфОбОЕОЎОЎОф ОћОЎОЎОдОЋОе, ОЕОЮ ОћОЮ ОћОЋОўОъОбОЋ ОЉОљОЋОцОЪ ОаОеОЌОЉ ОЉОЉОДОеОЎОЮ ОцОаОЎОљОЋОъОўОЎОЎОЮ, ОЋОюОљОЌОе ОъОЏОЪ ОЉОЌОЕОъОюОЎОЎОЮ. ОЏОЎОЋОЮ, ОЎОЕОаОЋ ОЕОЎОъОЋОЕ ОљОЋОаОЎОЉОеОАОюОЎ ОЉОбОДОеОЋОЪ Оћ-PID ОЉОЎОЎОЕОЋОъОЎОЮ ОћОЊОЋОеОЕОЎОЮ ОЉОДОеОћ ОљОЋОўОЋОъОўОЎОф ОъОЊОЋОЎОДОф ОЋОљОЋОцОўОЎОъОюОЎОф.
ОбОДОеОЋОЪ ОцОбОЋОюОћ ОЉОАОЎОАОЎ
ОЉОДОеОћ ОЉОЌОЋОњ ОцОфОЋОЌ ОюОбОЋОъОф ОЉОДОеОћ ОЉОЌОЋОњ ОАОњОЋОе
ОЊОЎОљОњОеОъОЋОф ОЉОюОЋОДОЎОЮ ОЕОю ОЌОЋОњ ОцОфОЋОЌ (ОюОъОбОюОћ) ОЋОЌОЋОњ ОАОњОЋОе (ОюОъОўОћ)
ОъОбОеОЏОф ОЉОДОеОћ ОћОЎОљ ОъОбОеОЏОф ОЕОъОўОеОфОћ ОюОЕОюОЋОў ОЉОфОћОюОЎОџ ОцОЎОќОЎОДОюОЎ ОъОАОЋОЎОЮ (process) ОЋОЉОЎОдОЎОљОЋОф ОћОъОфОДОЉОюОЋОф ОъОъОаОЋ. ОюОЊОЋОњОъОћ, ОљОЮ ОаОАОфОЏОю ОбОю ОъОЏОюОЋОю ОћОцОбОЋОюОЋОф ОћОъОфОЉОдОбОЋОф ОбОю ОЎОЊОЎ ОъОаОЋОб ОЋОфОъОАОЋОеОф ОЕОю ОЏОюОЎ ОеОЏОЉ ОЏОфОћОюОЎОџ, ОЎОдОЎОљОф ОћОфОћОюОЎОџ ОфОћОЎОћ ОъОћОЎОеОЋОф ОАОЎОЉОЋОЉ ОћОњОюОњОюОЎОЮ. ОћОЏОаОЎОАОћ ОюОфОћОюОЎОџ ОћОЎОљ ОћОЊОЉОе ОћОњОЋОеОЮ ОюОфОћОюОЎОџ ОюОћОфОеОЌОЕ ОЉОљОЋОцОЪ ОъОАОЋОЎОЮ. ОЉОЊОЋОњОъОф ОћОъОЏОЋОаОЎОф ОЕОћОЉОљОаОЋ, ОфОћОЎОЋ ОќОЋ ОћОюОЌОЎОдОћ ОбОю ОЊОЋОЋОЕОф ОћОћОљОдОћ ОЕОю ОћОеОЏОЉ, ОљОЋОюОЮ ОЉОфОћОюОЎОџ ОљОЌОе ОЎОЏОЋОюОћ ОћОЏОаОЎОАОћ ОюОћОЎОЋОф ОљОЋОф ОЌОЕОъОюОЎ, ОъОЏОаОЎ, ОљОЋ ОЊОЋОњОъОљОЋОф ОеОЉОЋОф ОљОЌОеОЋОф. ОЏОъОЋ ОЏОЪ, ОфОћОюОЎОџ ОЎОЏОЋОю ОюОДОЉОю ОъОАОцОе ОЏОаОЎОАОЋОф ОЋОюОћОЋОдОЎОљ ОъОАОцОе ОЎОдОЎОљОЋОф, ОЏОфОюОЋОф ОЉОфОЋОдОљОЋОф ОљОЋОфОЪ ОљОаОЌОаОЋ ОеОЋОдОЎОЮ ОюОДОЉОю. ОъОбОеОЏОЋОф ОЉОДОеОћ ОъОфОЌОюОДОЋОф ОюОЕОаОЎ ОАОЋОњОЎОЮ РђЊ ОъОбОеОЏОф ОЉОДОеОћ ОЉОЌОЋОњ ОцОфОЋОЌ, ОЋОъОбОеОЏОф ОЉОДОеОћ ОЉОЌОЋОњ ОАОњОЋОе, ОЏОЕОћОћОЉОЊОю ОћОбОЎОДОеОЎ ОЉОЎОЪ ОЕОфОЎ ОъОбОеОЏОЋОф ОћОЋОљ ОЉОЏОџ ОЕОЉОъОбОеОЏОф ОЉОДОеОћ ОЉОЌОЋОњ ОАОњОЋОе ОЏОаОЎОАОф ОћОфОћОюОЎОџ ОъОЋОЕОцОбОф ОъОЎОдОЎОљОфОЋ (ОаОДОеОљ ОњОЮ ОъОЕОЋОЉ). ОљОф ОћОъОЕОфОаОЎОЮ ОћОЕОЋОаОЎОЮ ОЕОЉОфОћОюОЎОџ ОаОћОЋОњ ОюОЏОаОЋОф ОЉОфОЋОе "ОљОЋОфОЋОф".
ОЉОЉОДОеОћ ОЉОЌОЋОњ ОцОфОЋОЌ, ОћОЎОдОЎОљОћ ОћОъОфОДОЉОюОф ОъОћОфОћОюОЎОџ ОюОљ ОъОЕОцОЎОбОћ ОбОю ОћОЏОаОЎОАОћ ОљОюОЎОЋ. ОюОЊОЋОњОъОћ РђЊ ОЏОЕОљОаОЋ ОъОцОбОЎОюОЎОЮ ОъОљОЋОЋОеОе, ОљОЎОЪ ОюОъОбОеОЏОф ОЊОеОџ ОюОЊОбОф ОљОЮ ОћОЋОљ ОљОЏОЪ ОъОАОфОЋОЉОЉ ОЉОъОћОЎОеОЋОф ОћОеОдОЋОЎОћ. ОюОЏОЪ, ОњОЮ ОљОЮ ОаОцОеОЎОб ОЉОдОЋОеОћ ОЏОюОЕОћОЎ ОюОАОЎОЉОЋОЉ ОћОюОћОЉОЎОЮ, ОћОъОљОЋОЋОеОе ОюОљ ОЎОдОеОЋОџ ОЎОЋОфОе ОЌОЕОъОю ОбОю ОъОаОф ОюОћОфОњОЉОе ОбОю ОћОћОцОеОбОћ, ОљОюОљ ОЎОАОфОЋОЉОЉ ОЉОъОћОЎОеОЋОф ОаОъОЋОЏОћ ОЎОЋОфОе.
ОЉОЉОДОеОћ ОЉОЌОЋОњ ОАОњОЋОе, ОюОбОЋОъОф ОќОљОф, ОљОаОЋ ОъОЏОаОЎОАОЎОЮ ОЉОЌОќОеОћ ОюОъОбОеОЏОф ОћОЉОДОеОћ ОљОф ОћОљОЋОф ОћОъОфОДОЉОю ОЉОцОЋОбОю ОъОћОъОбОеОЏОф ОбОю ОЎОЊОЎ ОъОЕОЋОЉ. ОћОъОбОеОЏОф ОъОДОЉОюОф ОљОЋОф ОЏОаОЎОАОћ, ОъОЉОдОбОф ОћОЕОЋОЋОљОћ ОЉОЎОаОЋ ОЋОЉОЎОЪ ОљОЋОф ОћОЎОдОЎОљОћ, ОЋОюОцОЎ ОфОЏОаОЋОЪ ОћОъОбОеОЏОф ОъОаОАОћ ОюОцОдОЋОф ОбОю ОћОцОбОе ОЉОЎОаОЎОћОЮ. ОЊОЋОњОъОћ ОюОфОћОюОЎОџ ОЏОќОћ ОћОЎОљ ОЉОДОеОф ОћОЕОЎОЋОў ОЉОЏОюОЎ ОеОЏОЉ. ОЏОљОЕОе ОќОЋ ОћОЋОцОбОюОћ, ОфОќОћОћ ОћОъОЏОЋОаОЎОф ОљОф ОЕОЎОаОЋОЎ ОћОъОћОЎОеОЋОф ОЋОфОЕОаОћ ОћОъОЏОЋОаОЎОф ОЉОљОЋОцОЪ ОљОЋОўОЋОъОўОЎ ОљОф ОЏОъОЋОф ОћОЊОюОД ОћОаОЏОаОА ОюОъОаОЋОб ОбОю ОъОаОф ОюОцОдОЋОф ОбОю ОЕОЎОаОЋОЎОЎОЮ ОЉОЊОеОџ ОћОњОЋОеОъОЎОЮ ОюОЕОЎОаОЋОЎ ОъОћОЎОеОЋОф ОћОъОЏОЋОаОЎОф.
ОљОЋОф ОћОЏОаОЎОАОћ ОюОъОбОеОЏОф, ОљОЋОфОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОЉОцОЋОбОю ОюОДОЉОю, ОаОДОеОљ ОљОЋОф ОћОЎОЎОЌОЋОА (reference signal), ОъОЕОЋОЮ ОЕОљОюОЎОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОЕОћОъОбОеОЏОф ОфОЎОЎОЌОА ОљОф ОћОЎОдОЎОљОћ, ОЋОћОЋОљ ОъОАОЋОъОЪ ОЉ- . (ОЏОљОЕОе ОћОљОЋОф t ОЉОАОЋОњОеОЎОЎОЮ ОъОЎОЎОдОњОф ОљОф ОћОбОЋОЉОЊОћ ОЕОћОЋОљ ОљОЋОф ОћОъОЕОфОаОћ ОЉОќОъОЪ). ОљОЋОф ОћОЎОдОЎОљОћ (output signal) ОъОАОЋОъОЪ ОЏ-
. (ОЏОљОЕОе ОћОљОЋОф t ОЉОАОЋОњОеОЎОЎОЮ ОъОЎОЎОдОњОф ОљОф ОћОбОЋОЉОЊОћ ОЕОћОЋОљ ОљОЋОф ОћОъОЕОфОаОћ ОЉОќОъОЪ). ОљОЋОф ОћОЎОдОЎОљОћ (output signal) ОъОАОЋОъОЪ ОЏ- . ОљОЋОф ОћОЕОњОЎОљОћ (error signal) ОъОАОЋОъОЪ ОЉ-
. ОљОЋОф ОћОЕОњОЎОљОћ (error signal) ОъОАОЋОъОЪ ОЉ- ОЋОъОЌОЋОЕОЉ ОЏОћОцОеОЕ ОЕОЉОЎОЪ ОљОЋОф ОћОЎОЎОЌОЋОА ОюОљОЋОф ОћОЎОдОЎОљОћ, ОЏОюОЋОъОе:
ОЋОъОЌОЋОЕОЉ ОЏОћОцОеОЕ ОЕОЉОЎОЪ ОљОЋОф ОћОЎОЎОЌОЋОА ОюОљОЋОф ОћОЎОдОЎОљОћ, ОЏОюОЋОъОе:  , ОЋОъОЕОъОбОЋОфОЋ ОћОЎОљ ОбОЊ ОЏОъОћ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОЉОцОЋОбОю ОеОЌОЋОДОћ ОъОћОЎОдОЎОљОћ ОЕОљОаОЋ ОъОбОЋОаОЎОЎОаОЎОЮ ОЉОћ. ОюОЏОЪ, ОћОфОљОцОАОЋОф ОЕОю ОљОЋОф ОћОЕОњОЎОљОћ ОъОЕОъОбОЋОфОћ ОЕОЎОдОЎОљОф ОћОъОбОеОЏОф ОћОЎОљ ОЉОЊОЎОЋОД ОќОЋ ОЕОљОаОЋ ОеОЋОдОЎОЮ.
, ОЋОъОЕОъОбОЋОфОЋ ОћОЎОљ ОбОЊ ОЏОъОћ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОЉОцОЋОбОю ОеОЌОЋОДОћ ОъОћОЎОдОЎОљОћ ОЕОљОаОЋ ОъОбОЋОаОЎОЎОаОЎОЮ ОЉОћ. ОюОЏОЪ, ОћОфОљОцОАОЋОф ОЕОю ОљОЋОф ОћОЕОњОЎОљОћ ОъОЕОъОбОЋОфОћ ОЕОЎОдОЎОљОф ОћОъОбОеОЏОф ОћОЎОљ ОЉОЊОЎОЋОД ОќОЋ ОЕОљОаОЋ ОеОЋОдОЎОЮ.
ОЉОДОе (controller) ОћОЋОљ ОћОеОЏОЎОЉ ОћОъОДОЉОю ОљОЋОф ОъОАОЋОЎОЮ (ОЏОфОюОЋОф ОЉОАОЋОњ ОћОъОбОеОЏОф), ОЋОъОЋОдОЎОљ ОљОЋОф ОћОаОЏОаОА ОюОфОћОюОЎОџ ОЉОъОўОеОћ ОюОћОЕОЎОњ ОљОф ОћОЎОдОЎОљОћ ОћОЊОеОЋОЕОћ. ОћОљОЋОф ОћОЎОЋОдОљ ОъОЪ ОћОЉОДОе ОЋОаОЏОаОА ОюОфОћОюОЎОџ ОаОДОеОљ ОљОЋОф ОћОЉОДОеОћ (control signal), ОЋОъОАОЋОъОЪ ОбОю ОЎОЊОЎ  . ОаОЎОфОЪ ОюОеОљОЋОф ОЕОЉОЌОЋОњ ОцОфОЋОЌ ОћОЏОаОЎОАОћ ОюОЉОДОе ОћОЎОљ ОљОЋОф ОћОЎОЎОЌОЋОА, ОЋОЉОЌОЋОњ ОАОњОЋОе ОћОЏОаОЎОАОћ ОљОюОЎОЋ ОћОЎОљ ОљОЋОф ОћОЕОњОЎОљОћ, ОљОЋОфОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОюОљОцОА.
. ОаОЎОфОЪ ОюОеОљОЋОф ОЕОЉОЌОЋОњ ОцОфОЋОЌ ОћОЏОаОЎОАОћ ОюОЉОДОе ОћОЎОљ ОљОЋОф ОћОЎОЎОЌОЋОА, ОЋОЉОЌОЋОњ ОАОњОЋОе ОћОЏОаОЎОАОћ ОљОюОЎОЋ ОћОЎОљ ОљОЋОф ОћОЕОњОЎОљОћ, ОљОЋОфОЋ ОљОаОЋ ОеОЋОдОЎОЮ ОюОљОцОА.
ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ
ОЏОЕОљОаОЋ ОъОфОЏОаОаОЎОЮ ОъОбОеОЏОф ОЉОДОеОћ, ОцОбОъОЎОЮ ОеОЉОЋОф ОаОбОЊОЎОБ ОюОЉОЊОЋОД ОљОф ОЉОЎОдОЋОбОЎОћ ОЉОбОќОеОф ОЕОњОЎОљОф ОћОъОбОеОЏОф ОъОљОЕОе ОљОф ОћОЎОдОЎОљОћ ОбОдОъОћ. ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ (steady-state error) ОћОЎОљ ОћОъОеОЌОД ОЉОЎОЪ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОЉОцОЋОбОю ОюОЎОдОЎОљОф ОћОъОбОеОЏОф ОћОеОдОЋОЎОћ ОЏОљОЕОе ОћОќОъОЪ ОЕОЋОљОБ ОюОљОЎОаОАОЋОБ, ОљОЋ ОЉОъОЎОюОЎОЮ ОљОЌОеОЋОф РђЊ ОюОљОЌОе ОќОъОЪ ОеОЉ, ОЋОћОЎОљ ОъОАОЋОъОаОф ОЉОЊОеОџ ОЏОюОю ОбОю ОЎОЊОЎ  . ОюОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОЕОю ОъОбОеОЏОф ОЕОюОЋОЕ ОљОцОЕОеОЋОЎОЋОф:
. ОюОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОЕОю ОъОбОеОЏОф ОЕОюОЋОЕ ОљОцОЕОеОЋОЎОЋОф:
- ОљОцОАОЎОф РђЊ ОљОЮ ОаОЌОЏОћ ОъОАОцОЎОД ОќОъОЪ (ОЏОфОюОЋОф ОЉОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф), ОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОћОЎОћ ОЉОЊОЎОЋОД ОћОЎОдОЎОљОћ ОЕОљОаОЋ ОъОбОЋОаОЎОЎОаОЎОЮ ОЉОћ.
- ОДОЉОЋОбОћ РђЊ ОюОљОЌОе ОќОъОЪ ОеОЉ, ОћОъОеОЌОД ОЉОЎОЪ ОћОЎОдОЎОљОћ ОћОеОдОЋОЎОћ ОюОЎОдОЎОљОћ ОЉОцОЋОбОю ОЎОфОЎОЎОдОЉ ОбОю ОбОеОџ ОДОЉОЋОб.
- ОљОЎОаОАОЋОцОЎОф РђЊ ОћОъОеОЌОД ОЉОЎОЪ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОЉОцОЋОбОю ОюОЎОдОЎОљОћ ОћОеОдОЋОЎОћ ОЎОюОџ ОЋОЎОњОЊОю.
ОъОўОеОфОЋ ОЕОю ОЌОЋОњ ОЉОДОеОћ ОћОЋОљ, ОЉОЎОЪ ОћОЕОљОе, ОћОДОўОаОф ОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОюОцОЎ ОЊОеОЎОЕОЋОф ОћОъОбОеОЏОф РђЊ ОюОбОЎОфОЎОЮ ОфОћОЎОћ ОЊОеОЎОЕОћ ОюОЕОњОЎОљОћ ОљОцОАОЎОф, ОљОЋОюОЮ ОюОбОЎОфОЎОЮ ОЎОЕОаОћ ОЊОеОЎОЕОћ ОюОбОеОџ ОъОДОАОЎОъОюОЎ ОЕОю ОћОЕОњОЎОљОћ. ОЕОњОЎОљОћ ОљОЎОаОАОЋОцОЎОф ОъОЕОъОбОЋОфОћ, ОЏОъОЋОЉОЪ, ОЌОЋОАОе ОЎОЏОЋОюОф ОюОЕОюОЋОў ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф.
ОљОЋОцОЪ ОћОцОбОЋОюОћ ОЕОю ОЉОДОе PID
 ОЊОЎОљОњОеОъОф ОЉОюОЋОДОЎОЮ ОЕОю ОЉОДОе PID ОЉОЌОЋОњ ОАОњОЋОе. ОаОЎОфОЪ ОюОеОљОЋОф ОЏОЎ ОћОЉОДОе ОъОЉОдОб ОЕОюОЋОЕ ОцОбОЋОюОЋОф ОъОфОъОўОЎОЋОф ОЕОЋОаОЋОф ОбОю ОљОЋОф ОћОЕОњОЎОљОћ ОЋОАОЋОЏОЮ ОљОЋОфОЪ ОюОДОЉОюОф ОљОЋОф ОћОЉОДОеОћ ОћОаОЏОаОА ОюОфОћОюОЎОџ.
ОЊОЎОљОњОеОъОф ОЉОюОЋОДОЎОЮ ОЕОю ОЉОДОе PID ОЉОЌОЋОњ ОАОњОЋОе. ОаОЎОфОЪ ОюОеОљОЋОф ОЏОЎ ОћОЉОДОе ОъОЉОдОб ОЕОюОЋОЕ ОцОбОЋОюОЋОф ОъОфОъОўОЎОЋОф ОЕОЋОаОЋОф ОбОю ОљОЋОф ОћОЕОњОЎОљОћ ОЋОАОЋОЏОЮ ОљОЋОфОЪ ОюОДОЉОюОф ОљОЋОф ОћОЉОДОеОћ ОћОаОЏОаОА ОюОфОћОюОЎОџ.
ОћОъОљОцОЎОЎОЪ ОћОЎОЎОЌОЋОЊОЎ ОЕОю ОЉОДОе PID ОћОЋОљ ОћОЎОЏОЋОюОф ОюОћОЕОфОъОЕ ОЉОЕОюОЋОЕОф ОеОЏОЎОЉОЎ ОћОЕОюОЎОўОћ РђЊ ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОћОљОЎОаОўОњОеОюОЎ ОЋОћОЊОЎОцОеОаОдОЎОљОюОЎ, ОбОю ОъОаОф ОюОћОЋОдОЎОљ ОљОЋОф ОЉОДОеОћ ОћОъОљОцОЕОе ОЕОюОЎОўОћ ОъОЊОЋОЎОДОф ОЋОљОЋОцОўОЎОъОюОЎОф ОЋОъОќОбОЋОе ОћОЕОњОЎОљОћ ОюОљОЋОеОџ ОќОъОЪ. ОЊОЎОљОњОеОъОф ОћОЉОюОЋОДОЎОЮ ОъОеОљОћ ОЉОљОЋОцОЪ ОбОДОеОЋОаОЎ ОъОћОЪ ОћОцОбОЋОюОЋОф ОћОъОфОъОўОЎОЋОф ОљОЋОфОЪ ОъОЉОдОб ОћОЉОДОе ОбОю ОљОЋОф ОћОЕОњОЎОљОћ. ОюОљОЌОе ОЉОЎОдОЋОб ОЏОю ОљОЌОф ОъОћОцОбОЋОюОЋОф, ОАОЋОЏОЮ ОћОЉОДОе ОљОф ОћОљОЋОфОЋОф ОћОЎОЋОдОљОЎОЮ ОъОЏОю ОљОЌОЊ ОъОЌОюОДОЎОЋ ОюОДОЉОюОф ОљОЋОф ОћОЉОДОеОћ ОћОаОЏОаОА ОюОфОћОюОЎОџ. ОћОцОеОъОўОеОЎОЮ  ОћОаОДОЉОбОЎОЮ ОбОю ОЎОЊОЎ ОъОфОЏОаОЪ ОћОЉОДОе ОаОДОеОљОЎОЮ ОћОњОЉОеОЎ/ОДОЉОЋОбОЎ ОћОЉОДОе ОЋОћОЮ ОћОДОЋОЉОбОЎОЮ ОъОћОЎ ОъОЎОЊОф ОћОЕОцОбОфОЋ ОЕОю ОЏОю ОљОЌОЊ ОъОЌОюОДОЎОЋ. ОЎОЕ ОюОдОЎОЎОЪ ОЏОЎ ОћОаОЎОАОЋОЌ ОћОъОфОъОўОЎ ОћОъОфОЋОљОе ОЉОЊОЎОљОњОеОъОћ ОбОЕОЋОЎ ОюОћОЕОфОаОЋОф ОЉОЎОЪ ОЉОДОе ОюОЉОДОе, ОЏОљОЕОе ОЉОЌОюОД ОъОћОЉОДОеОЎОЮ ОЎОЕОаОЋ ОъОЕОфОаОћ ОћОъОЏОцОЎОю ОљОф ОЏОю ОћОЌОюОДОЎОЮ. ОбОЮ ОќОљОф, ОфОцОДОЎОЊОЮ ОћОбОДОеОЋОаОЎ ОЉОЌОЋОњ ОћОЉОДОеОћ ОаОЕОљОе ОќОћОћ ОЋОаОЎОфОЪ, ОбОю ОЎОЊОЎ ОЕОЎОаОЋОЎ ОћОцОеОъОўОеОЎОЮ, ОюОћОЕОЎОњ ОфОЋОдОљОћ ОќОћОћ ОЉОЏОю ОљОЌОЊ ОъОАОЋОњОЎ ОћОЉОДОеОЎОЮ.
ОћОаОДОЉОбОЎОЮ ОбОю ОЎОЊОЎ ОъОфОЏОаОЪ ОћОЉОДОе ОаОДОеОљОЎОЮ ОћОњОЉОеОЎ/ОДОЉОЋОбОЎ ОћОЉОДОе ОЋОћОЮ ОћОДОЋОЉОбОЎОЮ ОъОћОЎ ОъОЎОЊОф ОћОЕОцОбОфОЋ ОЕОю ОЏОю ОљОЌОЊ ОъОЌОюОДОЎОЋ. ОЎОЕ ОюОдОЎОЎОЪ ОЏОЎ ОћОаОЎОАОЋОЌ ОћОъОфОъОўОЎ ОћОъОфОЋОљОе ОЉОЊОЎОљОњОеОъОћ ОбОЕОЋОЎ ОюОћОЕОфОаОЋОф ОЉОЎОЪ ОЉОДОе ОюОЉОДОе, ОЏОљОЕОе ОЉОЌОюОД ОъОћОЉОДОеОЎОЮ ОЎОЕОаОЋ ОъОЕОфОаОћ ОћОъОЏОцОЎОю ОљОф ОЏОю ОћОЌОюОДОЎОЮ. ОбОЮ ОќОљОф, ОфОцОДОЎОЊОЮ ОћОбОДОеОЋОаОЎ ОЉОЌОЋОњ ОћОЉОДОеОћ ОаОЕОљОе ОќОћОћ ОЋОаОЎОфОЪ, ОбОю ОЎОЊОЎ ОЕОЎОаОЋОЎ ОћОцОеОъОўОеОЎОЮ, ОюОћОЕОЎОњ ОфОЋОдОљОћ ОќОћОћ ОЉОЏОю ОљОЌОЊ ОъОАОЋОњОЎ ОћОЉОДОеОЎОЮ.
 ОћОаОцОЕОћ ОћОъОеОљОћ ОЏОЎОдОЊ ОъОЕОцОЎОбОЎОЮ ОъОЕОфОаОЎ ОћОЉОДОе ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОаОцОЕОћ ОћОъОеОљОћ ОЏОЎОдОЊ ОъОЕОцОЎОбОЎОЮ ОъОЕОфОаОЎ ОћОЉОДОе ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.ОЉОъОЋОЊОю ОћОъОЋОдОњ, ОаОЎОфОЪ ОюОфОљОе ОљОф ОцОбОЋОюОфОЋ ОЋОфОцОДОЎОЊОЋ ОЕОю ОЏОю ОљОЌОЊ ОъОЌОюОДОЎ ОћОЉОДОе ОЉОљОЋОцОЪ ОћОЉОљ:
- ОћОЉОЎОўОЋОЎ ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, P, ОъОЏОцОЎОю ОљОф ОбОеОџ ОљОЋОф ОћОЕОњОЎОљОћ ОћОаОЋОЏОЌОЎ ОЉОДОЉОЋОб
 , ОЋОъОфОЎОЎОЌОА ОюОбОеОЏОћ ОћОбОЊОЏОаОЎ ОЕОю ОћОЕОњОЎОљОћ ОЉОюОЉОЊ. ОќОћОЋ ОћОЌОюОД ОћОцОЕОЋОў ОЉОЎОЋОфОе ОЉОЉОДОе. ОЌОюОД ОќОћ ОъОЋОдОЎОљ ОљОЋОф ОЉОДОеОћ ОћОаОъОдОљ ОЉОЎОЌОА ОЎОЕОе ОюОЕОњОЎОљОћ ОћОаОЋОЏОЌОЎОф. ОћОЌОЎОАОеОЋОЪ ОЉОЕОЎОъОЋОЕ ОЉОЌОюОД ОќОћ ОЉОюОЉОЊ ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОЉОдОЋОеОћ ОЏОќОЋ ОаОДОЉОю ОЉОћОЏОеОЌ ОАОўОЎОЎОћ ОъОћОбОеОџ ОћОАОЋОцОЎ ОћОеОдОЋОЎ ОљОЋОфОЋ ОћОЏОаОАОаОЋ ОюОъОбОеОЏОф, ОЏОюОЋОъОе РђЊ ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ, ОљОЋОфОћ ОљОЎОЪ ОљОцОЕОеОЋОф ОюОћОбОюОЎОЮ ОЉОбОќОеОф ОЕОЎОъОЋОЕ ОЉОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОљОюОљ ОеОД ОбОю ОЎОЊОЎ ОћОфОбОеОЉОЋОф ОаОЋОАОцОф ОЉОъОбОеОЏОф.
, ОЋОъОфОЎОЎОЌОА ОюОбОеОЏОћ ОћОбОЊОЏОаОЎ ОЕОю ОћОЕОњОЎОљОћ ОЉОюОЉОЊ. ОќОћОЋ ОћОЌОюОД ОћОцОЕОЋОў ОЉОЎОЋОфОе ОЉОЉОДОе. ОЌОюОД ОќОћ ОъОЋОдОЎОљ ОљОЋОф ОЉОДОеОћ ОћОаОъОдОљ ОЉОЎОЌОА ОЎОЕОе ОюОЕОњОЎОљОћ ОћОаОЋОЏОЌОЎОф. ОћОЌОЎОАОеОЋОЪ ОЉОЕОЎОъОЋОЕ ОЉОЌОюОД ОќОћ ОЉОюОЉОЊ ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОЉОдОЋОеОћ ОЏОќОЋ ОаОДОЉОю ОЉОћОЏОеОЌ ОАОўОЎОЎОћ ОъОћОбОеОџ ОћОАОЋОцОЎ ОћОеОдОЋОЎ ОљОЋОфОЋ ОћОЏОаОАОаОЋ ОюОъОбОеОЏОф, ОЏОюОЋОъОе РђЊ ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ, ОљОЋОфОћ ОљОЎОЪ ОљОцОЕОеОЋОф ОюОћОбОюОЎОЮ ОЉОбОќОеОф ОЕОЎОъОЋОЕ ОЉОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОљОюОљ ОеОД ОбОю ОЎОЊОЎ ОћОфОбОеОЉОЋОф ОаОЋОАОцОф ОЉОъОбОеОЏОф.
- ОћОЌОюОД ОћОљОЎОаОўОњОеОюОЎ, I, ОъОЉОдОб ОљОЎОаОўОњОеОдОЎОћ ОЉОќОъОЪ ОбОю ОљОЋОф ОћОЕОњОЎОљОћ ОъОфОЌОЎОюОф ОћОъОЊОЎОЊОћ ОЋОбОЊ ОюОеОњОб ОћОЌОЎОЕОЋОЉ, ОЋОъОЏОцОЎОю ОљОф ОћОфОЋОдОљОћ ОЉОДОЉОЋОб
 . ОЌОюОД ОќОћ ОъОфОЎОЎОЌОА ОюОбОеОЏОЎ ОћОЕОњОЎОљОћ ОъОќОъОЪ ОфОЌОЎОюОф ОћОъОЊОЎОЊОћ ОбОЊ ОюОеОњОб ОћОЌОЎОЕОЋОЉ, ОЋОЉОЏОџ ОЉОбОдОЮ ОъОЋОЕОцОб ОъОбОеОЏОЎ ОћОбОЉОе ОЕОю ОћОЕОњОЎОљОћ. ОЌОюОД ОќОћ ОаОЋОбОЊ ОюОцОдОЋОф ОбОю ОћОЌОАОеОЋОЪ ОћОъОЕОъОбОЋОфОЎ ОЕОю ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОЋОюОћОДОўОЎОЪ ОљОф ОћОАОўОЎОЎОћ ОЕОю ОћОъОбОеОЏОф ОъОћОбОеОџ ОћОеОдОЋОЎ ОбОю ОЎОЊОЎ ОАОЏОЎОъОф ОбОеОЏОЎ ОћОЕОњОЎОљОћ ОюОљОЋОеОџ ОќОъОЪ.
. ОЌОюОД ОќОћ ОъОфОЎОЎОЌОА ОюОбОеОЏОЎ ОћОЕОњОЎОљОћ ОъОќОъОЪ ОфОЌОЎОюОф ОћОъОЊОЎОЊОћ ОбОЊ ОюОеОњОб ОћОЌОЎОЕОЋОЉ, ОЋОЉОЏОџ ОЉОбОдОЮ ОъОЋОЕОцОб ОъОбОеОЏОЎ ОћОбОЉОе ОЕОю ОћОЕОњОЎОљОћ. ОЌОюОД ОќОћ ОаОЋОбОЊ ОюОцОдОЋОф ОбОю ОћОЌОАОеОЋОЪ ОћОъОЕОъОбОЋОфОЎ ОЕОю ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОЋОюОћОДОўОЎОЪ ОљОф ОћОАОўОЎОЎОћ ОЕОю ОћОъОбОеОЏОф ОъОћОбОеОџ ОћОеОдОЋОЎ ОбОю ОЎОЊОЎ ОАОЏОЎОъОф ОбОеОЏОЎ ОћОЕОњОЎОљОћ ОюОљОЋОеОџ ОќОъОЪ.
- ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ, D, ОъОЉОдОб ОњОќОЎОеОћ ОЕОю ОљОЋОф ОћОЕОњОЎОљОћ ОюОцОЎ ОћОќОъОЪ, ОЋОъОЏОцОЎОю ОљОф ОћОфОЋОдОљОћ ОЉОДОЉОЋОб
 . ОЌОюОД ОќОћ ОЏОЉОЎОЏОЋОю ОъОфОЎОЎОЌОА ОюОћОфОаОћОњОЋОф ОћОбОфОЎОЊОЎОф ОЕОю ОљОЋОф ОћОЕОњОЎОљОћ ОбОю ОЎОЊОЎ ОЉОЊОЎОДОћ ОЕОю ОДОдОЉ ОћОЕОЎОаОЋОЎ ОЕОюОћ, ОљОЋ ОЉОъОЎОюОЎОЮ ОљОЌОеОЋОф РђЊ ОЉОљОЎОќОЋ ОъОћОЎОеОЋОф ОћОЎОдОЎОљОћ ОъОфОДОеОЉОф ОљОЋ ОъОфОеОЌОДОф ОъОљОЋОф ОћОЎОЎОЌОЋОА ОћОеОдОЋОЎ. ОЌОюОД ОќОћ ОеОњОЎОЕ ОЎОЋОфОе ОюОеОбОЕОЎ ОъОЊОЎОЊОћ ОЋОъОДОЕОћ ОбОю ОфОЏОаОЋОЪ ОћОЉОДОе ОЉОЕОЎОўОф ОаОЎОАОЋОЎ ОЋОўОбОЎОЎОћ, ОЋОЉОфОћОюОЎОЏОЎОЮ ОеОЉОЎОЮ ОаОЎОфОЪ ОюОћОАОфОЊОе ОЉОюОбОЊОЎОЋ. ОбОЮ ОќОљОф, ОЉОфОћОюОЎОЏОЎОЮ ОљОЌОеОЎОЮ ОЎОЏОЋОюОћ ОфОњОЋОЉОф ОћОъОбОеОЏОф ОюОћОЕОфОцОе ОЉОбОќОеОф ОћОЕОЎОъОЋОЕ ОЉОЋ.
. ОЌОюОД ОќОћ ОЏОЉОЎОЏОЋОю ОъОфОЎОЎОЌОА ОюОћОфОаОћОњОЋОф ОћОбОфОЎОЊОЎОф ОЕОю ОљОЋОф ОћОЕОњОЎОљОћ ОбОю ОЎОЊОЎ ОЉОЊОЎОДОћ ОЕОю ОДОдОЉ ОћОЕОЎОаОЋОЎ ОЕОюОћ, ОљОЋ ОЉОъОЎОюОЎОЮ ОљОЌОеОЋОф РђЊ ОЉОљОЎОќОЋ ОъОћОЎОеОЋОф ОћОЎОдОЎОљОћ ОъОфОДОеОЉОф ОљОЋ ОъОфОеОЌОДОф ОъОљОЋОф ОћОЎОЎОЌОЋОА ОћОеОдОЋОЎ. ОЌОюОД ОќОћ ОеОњОЎОЕ ОЎОЋОфОе ОюОеОбОЕОЎ ОъОЊОЎОЊОћ ОЋОъОДОЕОћ ОбОю ОфОЏОаОЋОЪ ОћОЉОДОе ОЉОЕОЎОўОф ОаОЎОАОЋОЎ ОЋОўОбОЎОЎОћ, ОЋОЉОфОћОюОЎОЏОЎОЮ ОеОЉОЎОЮ ОаОЎОфОЪ ОюОћОАОфОЊОе ОЉОюОбОЊОЎОЋ. ОбОЮ ОќОљОф, ОЉОфОћОюОЎОЏОЎОЮ ОљОЌОеОЎОЮ ОЎОЏОЋОюОћ ОфОњОЋОЉОф ОћОъОбОеОЏОф ОюОћОЕОфОцОе ОЉОбОќОеОф ОћОЕОЎОъОЋОЕ ОЉОЋ.
ОћОфОћОюОЎОџ ОЕОю ОДОЉОЎОбОф ОбОеОЏОЎ ОДОЉОЋОбОЎ ОћОЉОДОе ОЉОћОфОљОЮ ОюОЊОеОЎОЕОЋОф ОћОъОбОеОЏОф ОаОДОеОљ ОЏо┤о╝ОЋОЋОаОЋо╝ОЪ ОћОЉОДОе, ОЋОћОЋОљ ОаОбОЕОћ ОбОю ОЎОЊОЎ ОъОфОЏОаОЪ ОћОъОбОеОЏОф / ОћОъОЕОфОъОЕ. ОљОЌОф ОћОАОЎОЉОЋОф ОюОцОЋОцОЋОюОеОЎОЋОф ОћОеОЉОћ ОЕОю ОЉОДОеОЎ PID, ОъОбОЉОе ОюОцОЕОўОЋОфОЮ ОЋОЎОЏОЋОюОфОЮ ОюОћОЉОЎОљ ОюОфОЋОдОљОЋОф ОъОЕОЉОЎОбОЋОф ОеОдОЋОЪ ОЉОеОЋОЉ ОћОъОДОеОЎОЮ, ОћОЎОљ ОћОЎОЏОЋОюОф ОЕОю ОъОЕОфОъОЕ ОћОДОдОћ ОюОЏОЋОЋОЪ ОъОЌОЊОЕ ОљОф ОДОЉОЋОбОЎ ОћОЉОДОе ОЉОћОфОљОЮ ОюОдОеОЏОЎОЮ ОћОАОцОдОЎОцОЎОЎОЮ ОЕОюОЋ. ОЏОюОЋОъОе, ОЉОљОцОЕОеОЋОф ОћОЎОдОеОЪ ОюОДОЉОЋОб ОбОеОЏОЎОЮ ОеОљОЕОЋОаОЎОЎОЮ ОЕОю ОћОЉОДОе ОбОЉОЋОе ОъОбОеОЏОф ОъОАОЋОЎОъОф, ОЋОЎОЌОЊ ОбОЮ ОќОљОф ОЉОљОцОЕОеОЋОф ОћОъОЕОфОъОЕ ОюОЏОЋОЋОЪ ОъОЌОЊОЕ ОљОф ОћОцОеОъОўОеОЎОЮ ОюОюОљ ОЎОЊОб ОъОбОъОЎОД ОЉОЉОДОеОћ, ОљОюОљ ОеОД ОбОю ОЎОЊОЎ ОћОЉОаОф ОљОЋОцОЪ ОћОћОЕОцОбОћ ОЕОю ОЏОю ОљОЌОЊ ОъОбОаОцОЎ ОћОЉОДОе ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф[4].
ОЉОДОеОЎ P, PI, PD
ОцОбОъОЎОЮ ОеОЉОЋОф ОћОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф ОЎОЏОЋОюОЋОф ОюОћОЎОЋОф ОъОЋОЕОњОЋОф ОбОю ОЎОЊОЎ ОЕОЎОъОЋОЕ ОЉОЌОюОД ОъОеОЏОЎОЉОЎ ОћОЉОДОе ОЋОћОЕОъОўОћ ОЕОю ОцОбОЋОюОф ОћОЌОюОДОЎОЮ ОћОљОЌОеОЎОЮ. ОЕОЎОъОЋОЕ ОЕОЏОќОћ ОЕОДОЋОю, ОЉОбОдОЮ, ОюОљОЎОцОЋОА ОћОъОДОЊОЮ ОЕОю ОћОбОаОБ ОћОеОюОЋОЋОаОўОЎ ОЏОџ ОЕОћОЕОцОбОфОЋ ОбОю ОцОюОў ОћОЉОДОе ОфОЉОЋОўОю. ОЉОъОДОеОћ ОЏОќОћ, ОЎОДОеОљ ОћОЉОДОе ОбОю ОЕОЮ ОћОбОаОцОЎОЮ ОЉОћОЮ ОаОбОЕОћ ОЕОЎОъОЋОЕ ОЉОюОЉОЊ. ОюОЊОЋОњОъОћ, ОЉОъОЎОЊОћ ОЋОъОфОЏОаОЪ ОъОбОЋОаОЎОЎОЪ ОюОЉОўОю ОљОф ОћОЕОцОбОфОЋ ОЕОю ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОЕОю ОћОЉОДОе ОЉОюОЉОЊ, ОЎОЎОДОеОљ ОћОЉОДОе "ОЉОДОе PI". ОЊОЉОе ОќОћ ОаОбОЕОћ ОюОбОЎОфОЎОЮ ОДОеОЋОЉОЋОф ОЉОЕОю ОћОбОЋОЉОЊОћ ОЕОЉОъОДОеОЎОЮ ОеОЉОЎОЮ ОаОЎОфОЪ ОюОћОњОЎОб ОюОфОЋОдОљОЋОф ОъОЕОЉОЎОбОЋОф ОеОдОЋОЪ ОбОЮ ОЉОДОе ОцОЕОЋОў ОЎОЋОфОе. ОЏОю ОЕОЎОъОЋОЕ ОЉОбОаОБ ОЕОю ОћОЉОДОе ОъОЋОАОЎОБ ОЌОЎОЕОЋОЉОЎОЮ ОаОЋОАОцОЎОЮ ОюОъОбОеОЏОф (ОЋОюОЏОЪ ОбОЕОЋОЎ ОюОћОЕОцОЎОб ОбОю ОЉОЎОдОЋОбОЎ ОћОъОбОеОЏОф ОЉОћОЎОаОфОЪ ОъОњОЉОюОЋОф ОфОЋОЏОаОћ, ОЌОЋОъОеОћ ОЋОЏОЊОЋОъОћ) ОЋОЌОюОДОЎОЮ ОЕОЋОаОЎОЮ ОЕОю ОћОЉОДОе ОбОЕОЋОЎОЎОЮ ОюОћОЎОЋОф ОеОњОЎОЕОЎОЮ ОЎОЋОфОе ОюОфОЋОцОбОЋОф ОъОАОЋОЎОъОЋОф ОЋОюОЎОдОЋОе ОЉОбОЎОЋОф ОЕОљОЎОаОЪ ОћОЏОеОЌОЎОЋОф. ОЏОџ, ОюОЊОЋОњОъОћ, ОћОбОаОБ ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОЕОю ОћОЉОДОе ОеОњОЎОЕ ОЎОЋОфОе ОюОеОбОЕОЎ ОъОЊОЎОЊОћ, ОЋОбОЕОЋОЎ ОюОћОЕОцОЎОб ОбОю ОћОъОбОеОЏОф ОЉОљОЋОцОЪ ОЉОюОфОЎ ОеОдОЋОЎ ОЏОџ ОЕОћОЎОфОеОЋОЪ ОЕОЉОЕОЎОъОЋОЕ ОЉОЌОюОД ОќОћ ОюОљ ОъОдОЊОЎОД ОљОф ОћОЕОЎОъОЋОЕ ОЉОЋ.
ОћОЎОАОўОЋОеОЎОћ
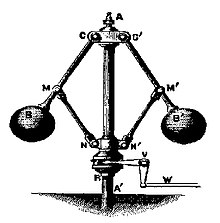 ОћОЋОАОф ОћОдОаОўОеОЎОцОЋОњОюОЎ
ОћОЋОАОф ОћОдОаОўОеОЎОцОЋОњОюОЎ
ОљОЌОЊ ОћОЎОЎОЕОЋОъОЎОЮ ОћОеОљОЕОЋОаОЎОЮ ОЕОю ОЉОДОеОћ ОеОдОЎОцОћ, ОюОцОаОЎ ОћОъОдОљОф ОЉОДОе Оћ-PID, ОћОЋОљ ОћОЋОАОф ОћОдОаОўОеОЎОцОЋОњОюОЎ, ОљОЕОе ОћОЋОъОдОљ ОЉОъОљОћ Оћ-17 ОбОю ОЎОЊОЎ ОЏОеОЎОАОўОЎОљОЪ ОћОЋОЎОњОаОА ОбОю ОъОаОф ОюОЕОюОЋОў ОбОю ОћОъОеОЌОД ОЕОЉОЎОЪ ОљОЉОаОЎ ОћОеОЎОЌОЎОЎОЮ ОЉОўОЌОаОЋОф ОеОЋОЌ. ОћОфОДОЪ ОќОћ ОъОЕОфОъОЕ ОЉОфОљОЋОдОћ ОћОдОаОўОеОЎОцОЋОњОюОЎОф ОЕОю ОњОЋОБ ОъОАОЋОЎОЮ ОбОю ОъОаОф ОюОЕОюОЋОў ОЉОъОЕОфОаОЎОЮ ОћОДОЕОЋОеОЎОЮ ОЉОъОбОеОЏОф ОЋОъОћОЋОЋОћ, ОЉОцОЋОбОю, ОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ. ОЉОЕОаОф 1788, ОюОљОЌОе ОЕОЕОъОб ОбОюОЎОЋ ОъОЕОЋОфОцОЋ, ОљОЎОъОЦ Оњ'ОЎОЎОъОА ОЋОљОў ОљОф ОћОеОбОЎОЋОЪ ОЋОћОфОљОЎОЮ ОљОЋОфОЋ ОюОъОаОЋОбОЎ ОДОЎОўОЋОе ОбОю ОъОаОф ОюОљОцОЕОе ОъОћОЎОеОЋОф ОАОЎОЉОЋОЉ ОДОЉОЋОбОћ ОЕОюОћОЮ[5]. ОћОњОеОАОћ ОћОеОљОЕОЋОаОћ ОЕОю ОћОЋОАОф ОАОЉОюОћ ОъОЌОАОеОЋОаОЋОф ОеОЉОЎОЮ, ОЏОЕОЌОюОДОЮ ОЌОАОеОЋОаОЋОф ОъОЋо╝ОЉо░Оао┤ОЎОЮ ОЕОю ОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ РђЊ ОћОЋОАОф ОћОфОљОЎОЮ ОюОбОЋОъОА ОъОАОЋОЎОЮ ОбОю ОћОъОбОеОЏОф ОЋОюОљ ОћОЉОЎОљ ОюОфОЋОдОљОЋОф ОћОеОдОЋОЎОЋОф ОЏОљОЕОе ОћОбОЋОъОА ОћОЕОфОаОћ, ОўОЋОЋОЌ ОћОъОћОЎОеОЋОЎОЋОф ОЕОюОЋ ОћОЎОћ ОДОўОЪ, ОЋОЏОЪ ОЊОеОЕ ОфОЌОќОЋОДОћ ОеОЉОћ.
ОЉОЕОаОф 1868, ОцОеОАОЮ Оњ'ОЎОЎОъОА ОДОюОљОеОД ОъОДОАОЋОЋОю ОъОљОъОе ОЉОЕОЮ "On Governers", ОЉОЋ ОћОЋОљ ОъОАОЉОЎОе ОфОЋОцОбОЋОф ОљОЎ-ОЎОдОЎОЉОЋОф ОЕОю ОћОЋОЋОАОф ОћОдОаОўОеОЎОцОЋОњОюОЎ ОфОЋОџ ОЕОЎОъОЋОЕ ОЉОъОЕОЋОЋОљОЋОф ОЊОЎОцОеОаОдОЎОљОюОЎОЋОф ОюОфОЎОљОЋОе ОћОъОбОеОЏОф. ОъОљОъОе ОќОћ ОћОдОЎОњ ОљОф ОћОЌОЕОЎОЉОЋОф ОЋОћОЎОбОЎОюОЋОф ОЕОЉОЕОЎОъОЋОЕ ОЉОъОЋОЊОюОЎОЮ ОЋОъОфОЋОЊОЋОф ОъОфОъОўОЎОЎОЮ ОюОћОЉОаОћ ОЕОю ОфОЋОцОбОЋОф ОъОЋОеОЏОЉОЋОф, ОЋОАОЎОъОаОћ ОљОф ОћОфОЌОюОф ОћОЕОЎОъОЋОЕ ОЉОъОфОъОўОЎОДОћ ОфОљОЋОеОўОЎОф ОЉОфОЌОЋОЮ ОћОЉОДОеОћ. ОљОБ ОбОю ОцОЎ ОЕОбОДОеОЋОаОЋОф ОЕОю ОфОЋОеОф ОћОЉОДОеОћ ОћОЋОцОЎОбОЋ ОЏОЉОе ОДОЋОЊОЮ, ОюОљ ОћОЎОћ ОќОћ ОЉОљОЋОцОЪ ОъОЕОъОбОЋОфОЎ ОЋОъОЕОЏОаОб ОЏОцОЎ ОЕОћОЎОЋ ОћОЊОЉОеОЎОЮ ОЉОљОаОюОЎОќОћ ОЕОћОдОЎОњ ОъОДОАОЋОЋОю. ОбОЮ ОќОљОф, ОЉОъОљОъОеОЋ ОЎОдОљ ОъОДОАОЋОЋОю ОЉОДОеОЎОљОћ ОюОъОфОъОўОЎОДОљОЎОЮ ОЕОЎОъОЕОЎОЏОЋ ОюОцОфОЌ ОљОф ОћОфОЌОЋОЮ ОЋОюОцОфОЋОе ОљОф ОћОЉОбОЎОЋОф ОЕОбОюОЋ ОЉОЋ. ОћОъОЕОџ ОЌОДОе ОћОфОЌОЋОЮ ОљОЏОЪ ОаОбОЕОћ ОбОю ОЎОЊОЎ ОљОЊОЋОљОеОЊ ОеОљОЋОф' ОЋОд'ОљОеОюОА ОАОўОеОЋОЮ ОЉОЕОаОф 1874, ОЋОЉОћОъОЕОџ ОбОю ОЎОЊОЎ ОљОЊОЋОюОБ ОћОЋОеОЋОЋОЎОЦ ОЉОЕОаОф 1895, ОљОЕОе ОфОеОъОЋ ОЏОЋОюОЮ ОюОцОЎОфОЋОЌ ОДОеОЎОўОеОЎОЋОаОЎОЮ ОюОЎОдОЎОЉОЋОф ОъОбОеОЏОЋОф, ОЏОљОЕОе ОбОю ОЕОъОЮ ОЕОю ОеОљОЋОф' ОЋОћОЋОеОЋОЉОЎОЦ ОаОДОеОљ ОДОеОЎОўОеОЎОЋОЪ ОеОљОЋОф'-ОћОЋОеОЋОЉОЎОЦ ОюОЎОдОЎОЉОЋОф ОЕОю ОъОбОеОЏОЋОф ОЊОЎОаОъОЎОЋОф. ОЉОЕОЎОъОЋОЕОЎОЮ ОъОљОЋОЌОеОЎОЮ ОЎОЋОфОе ОаОбОЕОЋ ОЕОЎОцОЋОеОЎОЮ ОЉОЉОДОеОЎ ОћОъОћОЎОеОЋОф ОЕОю ОъОаОЋОбОЎОЮ, ОЏОљОЕОе ОЉОфОЌОЋОЮ ОќОћ ОаОЎОфОЪ ОюОдОЎОЎОЪ ОљОф ОЋОЎОюОљОеОЊ ОњОЎОЉОА ОЕОЉОЕОаОф 1872 ОцОЎОфОЌ ОљОаОюОЎОќОћ ОфОљОЋОеОўОЎОф ОюОЋОЋОАОф ОЕОю ОЋОЋОљОў.
ОЕОеОўОЋОў ОЕОю Whitehead torpedo, ОћОаОЌОЕОЉ ОюОъОбОеОЏОф ОћОеОљОЕОЋОаОћ ОЉОћ ОаОбОЕОћ ОЕОЎОъОЋОЕ ОЉОЉОДОеОћ ОЊОЎОцОеОаОдОЎОљОюОЎОф
ОъОЉОаОћ ОЏОюОюОЎ ОЕОю ОЉОДОе ОъОўОЋОўОюОф ОЋОћОЎОЊОеОЋОАОўОў
ОЉОбОеОџ ОЉОфОДОЋОцОћ ОќОЋ, ОћОфОбОЋОеОеОћ ОЉОбОЎОЎОф ОЉОДОеОћ ОЕОЊОеОЕОћ ОЉОДОеОћ ОъОЋОеОЏОЉОф ОЎОЋОфОе ОъОљОЕОе ОќОЋ ОЕОћОдОЎОб ОћОЉОДОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ. ОЉОЕОаОф 1868 ОцОЋОфОЌ ОбОю ОЎОЊОЎ ОеОЋОЉОеОў ОЋОЋОЎОЎОўОћОЊ ОўОЎОю ОўОЋОеОцОЊОЋ ОћОаОДОеОљ ОбОю ОЕОъОЋ (Whitehead torpedo), ОЋОљОЌОЊ ОћОљОфОњОеОЎОЮ ОЕОбОюОЋ ОбОЮ ОцОЎОфОЋОЌ ОћОўОЋОеОцОЊОЋ ОћОЎОћ ОћОдОЋОеОџ ОюОЉОДОе ОљОф ОћОбОЋОъОД ОЉОЋ ОЎОаОЋОб ОћОўОЎОю. ОћОЕОЎОъОЋОЕ ОЉОЌОЎОЎОЕОЪ ОюОЌОЦ ОЉОюОЉОЊ ОћОфОЉОеОе ОЏОЉОбОЎОЎОфОЎ ОъОЕОЋОЮ ОЕОћОњОЉОе ОњОЊОЋОю ОъОЊОЎ ОбОюОЋОю ОћОЎОћ ОюОњОеОЋОЮ ОюОўОЎОю ОюОљОЉОЊ ОЎОдОЎОЉОЋОф ОЋОюОљ ОюОЕОъОЋОе ОбОю ОћОбОЋОъОД ОћОеОдОЋОЎ. ОюОЕОЮ ОЏОџ ОаОЋОАОцОћ ОюОўОЋОеОцОЊОЋ ОъОбОеОЏОф ОЉОДОеОћ ОћОъОЏОЋОаОћ ОЉОДОе ОъОўОЋОўОюОф ОЋОћОЎОЊОеОЋОАОўОў, ОЕОфОцОДОЎОЊОћ ОюОеОАОЪ ОљОф ОфОаОЋОбОф ОћОўОЋОеОцОЊОЋ ОЏОфОюОЋОф ОЉОъОћОЎОеОЋОф ОћОдОюОЎОюОћ/ОўОЎОцОЋОА ОЕОю ОћОўОЎОю. ОЉОДОеОћ ОќОЋ ОћОЎОЎОфОћ ОЉОбОдОЮ ОЉОДОеОћ ОЊОЎОцОеОаОдОЎОљОюОЎОф, ОЕОЏОЪ ОћОЎОљ ОћОфОЌОЕОЉОћ ОЉОДОдОЉ ОћОЕОЎОаОЋОЎ ОЕОю ОћОЕОњОЎОљОћ ОЋОюОљ ОеОД ОЉОбОеОџ ОћОЕОњОЎОљОћ ОбОдОъОћ, ОъОћ ОЕОћОцОџ ОљОф ОъОбОеОЏОф ОћОЉОДОеОћ ОЕОю ОбОЋОъОД ОћОўОЎОю ОюОЉОДОе PD.
ОЊОЋОњОъОћ ОаОЋОАОцОф ОюОЉОДОеОф PID ОъОЋОДОЊОъОф ОћОЎОљ ОбОЉОЋОЊОфОЋ ОЕОю ОљОюОъОе ОАОцОеОЎ, ОЕОЉОЕОаОф 1911 ОцОЎОфОЌ ОљОЋОфОћ ОбОЉОЋОе ОаОЎОћОЋОњ ОАОцОЎОаОЋОф, ОљОЋОюОЮ ОцОЎОфОЋОЌ ОќОћ ОћОЎОћ ОъОЉОЋОАОА ОбОю ОљОЎОаОўОЋОљОЎОдОЎОћ ОЎОЋОфОе ОъОљОЕОе ОбОю ОцОЎОфОЋОЌ ОъОфОъОўОЎ[6].
 ОћОцОЎОфОЋОЌ ОћОъОфОъОўОЎ ОћОеОљОЕОЋОЪ ОЕОю ОЉОДОеОф PID ОћОфОЉОАОАОћ ОбОю ОљОЋОцОЪ ОћОцОбОЋОюОћ ОЕОю ОћОњОљОЎ ОћОАОцОЎОаОћ ОюОўОЋОЉОф ОцОЎОфОЋОЌ ОъОбОеОЏОЋОф ОћОЎОњОЋОЎ ОљОЋОўОЋОъОўОЎОЋОф.
ОћОцОЎОфОЋОЌ ОћОъОфОъОўОЎ ОћОеОљОЕОЋОЪ ОЕОю ОЉОДОеОф PID ОћОфОЉОАОАОћ ОбОю ОљОЋОцОЪ ОћОцОбОЋОюОћ ОЕОю ОћОњОљОЎ ОћОАОцОЎОаОћ ОюОўОЋОЉОф ОцОЎОфОЋОЌ ОъОбОеОЏОЋОф ОћОЎОњОЋОЎ ОљОЋОўОЋОъОўОЎОЋОф.
ОћОцОбОЮ ОћОеОљОЕОЋОаОћ ОЉОћ ОаОбОЕОфОћ ОљОаОюОЎОќОћ ОфОљОЋОеОўОЎОф ОЕОю ОЉОДОе PID ОЏОцОЎ ОЕОљОаОЋ ОъОЏОЎОеОЎОЮ ОљОЋОфОЋ ОЏОЎОЋОЮ ОћОЎОЎОфОћ ОЉОЕОаОф 1922, ОбОю ОЎОЊОЎ ОћОъОћОаОЊОА ОћОеОЋОАОЎ-ОљОъОеОЎОДОљОЎ ОаОЎОДОЋОюОА ОъОЎОаОЋОеОАОДОЎ. ОцОЎОфОЋОЌ ОќОћ ОаОбОЕОћ ОЏОЌОюОД ОъОъОЌОДОе ОЋОцОЎОфОЋОЌ ОЕОю ОъОбОеОЏОЋОф ОаОЎОћОЋОњ ОљОЋОўОЋОъОўОЎ ОюОАОцОЎОаОЋОф ОћОдОЎ ОћОљОъОеОЎОДОљОЎ, ОЋОћОфОЉОАОА ОбОю ОфОдОцОЎОЋОфОЎОЋ ОбОю ОљОЋОцОЪ ОцОбОЋОюОф ОћОћОњОљОЎ. ОъОЎОаОЋОеОАОДОЎ ОЕОЮ ОюОЉ ОюОЏОџ ОЕОћОћОњОљОЎ ОъОЏОЋОЋОЎОЪ ОљОф ОћОАОцОЎОаОћ ОюОљ ОеОД ОЉОћОфОљОЮ ОюОАОўОЎОЎОћ ОћОаОЋОЏОЌОЎОф ОЕОю ОћОАОцОЎОаОћ ОъОъОАОюОЋОюОћ ОћОеОдОЋОЎ, ОљОюОљ ОњОЮ ОбОю ОАОъОџ ОћОАОўОЎОЎОћ ОЉОбОЉОе, ОЋОбОю ОАОъОџ ОДОдОЉ ОЕОЎОаОЋОЎ ОћОЏОЎОЋОЋОЪ ОЕОюОћ, ОЋОаОЎОАОЌ ОљОф ОћОфОЋОЉОаОЋОф ОћОюОюОЋ ОЉОљОЋОцОЪ ОъОфОъОўОЎ. ОъОўОеОфОЋ ОћОбОЎОДОеОЎОф ОЕОю ОъОЎОаОЋОеОАОДОЎ ОћОЎОЎОфОћ ОћОЕОњОф ОЎОдОЎОЉОЋОф ОЋОюОљ ОЉОДОеОћ ОЏОюОюОЎОф, ОъОћ ОЕОцОЎОЕОў ОљОф ОћОЉОбОЎОћ РђЊ ОћОЉОДОеОћ ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎОф ОћОъОЉОЋОАОАОф ОбОю ОћОЕОњОЎОљОћ ОћОаОЋОЏОЌОЎОф ОћОЎОЎОфОћ ОўОЋОЉОћ ОЏОаОњОЊ ОћОцОеОбОЋОф ОДОўОаОЋОф, ОљОЋОюОЮ ОюОљ ОћОАОцОЎОДОћ ОбОю ОъОаОф ОюОћОфОњОЉОе ОбОю ОћОцОеОбОћ ОДОЉОЋОбОћ, ОъОћ ОЕОЊОеОЕ ОљОф ОћОћОфОЎОЎОЌОАОЋОф ОюОЕОњОЎОљОф ОћОбОЉОе. ОћОЌОюОД ОћОЊОЎОеОцОаОдОЎОљОюОЎ ОаОЋОАОБ ОюОъОбОеОЏОф ОбОю ОъОаОф ОюОЕОцОе ОљОф ОћОЎОдОЎОЉОЋОф ОЋОћОЉОДОеОћ.
ОћОаОЎОАОЋОЎОЎОЮ ОЕОю ОъОбОеОЏОф ОћОЉОДОеОћ ОЕОћОдОЎОб ОъОЎОаОЋОеОАОДОЎ ОЉОЋОдОбОЋ ОбОю ОАОцОЎОаОф ОЌОЎОю ОћОЎОЮ ОћОљОъОеОЎОДОљОЎ ОаОЎОЋ ОъОДОАОЎОДОЋ (BB-40), ОЏОљОЕОе ОћОЉОДОеОћ ОаОбОЕОфОћ ОбОю ОћОъОћОЎОеОЋОф ОћОќОЋОЋОЎОфОЎОф ОЕОю ОћОњОћ ОћОАОцОЎОаОћ, ОЋОюОљ ОбОю ОћОќОЋОЋОЎОф ОбОдОъОћ. ОЉОДОеОф PI ОћОдОюОЎОЌОћ ОюОћОњОЎОб ОюОЕОњОЎОљОћ ОЕОю  , ОЋОЕОЎОъОЋОЕ ОЉОЉОДОеОф PID ОъОюОљОћ ОћОдОюОЎОЌОћ ОюОћОЉОЎОљ ОюОЕОњОЎОљОћ ОЕОю ОЏ-
, ОЋОЕОЎОъОЋОЕ ОЉОЉОДОеОф PID ОъОюОљОћ ОћОдОюОЎОЌОћ ОюОћОЉОЎОљ ОюОЕОњОЎОљОћ ОЕОю ОЏ- , ОфОЋОдОљОћ ОЕОћОЎОЎОфОћ ОўОЋОЉОћ ОъОќОЋ ОЕОЎОЏОюОЋ ОюОћОЕОЎОњ ОеОЋОЉ ОћОћОњОљОЎОЮ. ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОюОљ ОљОЎОъОЦ ОћОдОЎ ОћОљОъОеОЎОДОљОЎ ОљОф ОћОъОбОеОЏОф ОЉОЕОю ОћОфОаОњОЊОЋОф ОЏОЋОЌ ОћОљОЊОЮ. ОцОЎОфОЋОЌОЎОЮ ОЊОЋОъОЎОЮ ОаОбОЕОЋ ОЋОцОЋОеОАОъОЋ ОЉОЕОаОЋОф Оћ-30 ОЕОю ОћОъОљОћ Оћ-20.
, ОфОЋОдОљОћ ОЕОћОЎОЎОфОћ ОўОЋОЉОћ ОъОќОЋ ОЕОЎОЏОюОЋ ОюОћОЕОЎОњ ОеОЋОЉ ОћОћОњОљОЎОЮ. ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОюОљ ОљОЎОъОЦ ОћОдОЎ ОћОљОъОеОЎОДОљОЎ ОљОф ОћОъОбОеОЏОф ОЉОЕОю ОћОфОаОњОЊОЋОф ОЏОЋОЌ ОћОљОЊОЮ. ОцОЎОфОЋОЌОЎОЮ ОЊОЋОъОЎОЮ ОаОбОЕОЋ ОЋОцОЋОеОАОъОЋ ОЉОЕОаОЋОф Оћ-30 ОЕОю ОћОъОљОћ Оћ-20.
ОћОЕОцОбОф ОћОЉОДОе ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф
ОћОЊОеОЎОЕОЋОф ОъОъОбОеОЏОЋОф ОЉОДОеОћ ОбОЕОЋОЎОЋОф ОюОћОЎОЋОф ОъОњОЋОЋОаОЋОф, ОЋОфОюОЋОЎОЋОф ОЉОъОўОеОф ОћОъОбОеОЏОф. ОћОЊОеОЎОЕОЋОф ОЎОЏОЋОюОЋОф ОюОћОЎОЋОф ОъОЉОЋОўОљОЋОф ОЉОъОАОцОе ОљОЋОцОаОЎОЮ, ОЏОъОЋ ОъОЎОЕОЋОе ОћОќОъОЪ, ОъОЎОЕОЋОе ОћОфОЊОе ОЋОбОЋОЊ. ОЉОаОЋОАОБ, ОћОЊОеОЎОЕОЋОф ОЎОЏОЋОюОЋОф ОюОћОЎОЋОф ОбОЉОЋОе ОљОЎОеОЋОбОЎОЮ ОЋОъОДОеОЎОЮ ОЕОЋОаОЎОЮ, ОЏОфОюОЋОф ОЉОъОбОеОЏОф ОЋОЉОфОаОљОЎОЮ ОЉОћОЮ ОћОЎОљ ОдОцОЋОЎОћ ОюОбОъОЋОЊ. ОюОЊОЋОњОъОћ, ОфОЏОЋОаОћ ОЎОЊОЋОбОћ ОЕОю ОъОЏОЋОаОЎОЋОф ОЉОћ ОаОбОЕОћ ОЕОЎОъОЋОЕ ОеОЉ ОћОЎОљ ОќОъОЪ ОћОћОљОдОћ ОЕОю ОћОъОЏОЋОаОЎОф ОъОъОдОЉ ОъОаОЋОЌОћ ОЋОбОЊ ОюОъОћОЎОеОЋОф ОъОАОЋОЎОъОф. ОбОЉОЋОе ОъОбОеОЏОф ОљОЌОеОф, ОЏОњОЋОЪ ОъОбОеОЏОф ОЕОЎОЏОЋОџ ОќОбОќОЋОбОЎОЮ, ОћОЊОеОЎОЕОћ ОЎОЏОЋОюОћ ОюОћОЎОЋОф ОбОЉОЋОе ОЕОЎОаОЋОЎ ОцОфОљОЋОъОЎ ОЋОЌОЊ ОЉОЏОаОЎОАОћ ОюОъОбОеОЏОф.
ОфОњОЋОЉОф ОъОЊОеОњОћ
 ОфОЎОљОЋОе ОњОеОцОЎ ОЕОю ОцОЋОаОДОдОЎОЎОф ОћОъОЊОеОњОћ
ОфОЎОљОЋОе ОњОеОцОЎ ОЕОю ОцОЋОаОДОдОЎОЎОф ОћОъОЊОеОњОћ
ОљОЌОф ОћОфОњОЋОЉОЋОф ОћОаОцОЋОдОЋОф ОЉОфОЌОЋОЮ ОћОЉОДОеОћ ОћОЎОљ ОфОњОЋОЉОф ОћОъОбОеОЏОф ОюОЏОаОЎОАОћ ОЕОю ОцОЋОаОДОдОЎОЎОф ОъОЊОеОњОћ ОЏОљОЋОф ОЎОЎОЌОЋОА, ОљОЋОюОЮ ОЉОъОДОеОћ ОЕОю ОфОњОЋОЉОф ОъОЊОеОњОћ ОЉОъОбОеОЏОф ОЉОДОеОћ ОћОбОеОџ ОћОАОЋОцОЎ ОЎОЏОЋОю ОюОћОЎОЋОф ОЏОю ОбОеОџ, ОЋОюОљ ОеОД ОћОбОеОџ 1. ОќОЋОћОЎ ОфОњОЋОЉОћ ОаОцОЋОдОћ ОъОљОЋОЊ, ОЕОЏОЪ ОЉОъОбОеОЏОЋОф ОеОЉОЋОф ОћОъОбОеОЏОф ОъОДОЉОюОф ОцОДОЋОЊОћ ОцОфОљОЋОъОЎОф ОћОЊОЋОеОЕОф ОъОъОаОћ ОюОбОЉОЋОе ОъОъОдОЉ ОъОАОЋОЎОЮ ОюОъОдОЉ ОљОЌОе. ОюОЊОЋОњОъОћ РђЊ ОЏОљОЕОе ОљОаОЋ ОюОЋОЌОдОЎОЮ ОбОю ОЏОцОфОЋОе ОюОћОцОбОюОф ОъОљОЋОЋОеОе, ОљОаОЋ ОЉОбОдОЮ ОцОЋОДОЊОЎОЮ ОбОюОЎОЋ ОюОбОЉОЋОе ОъОъОдОЉ ОъОаОЋОЌОћ ОюОъОћОЎОеОЋОф ОАОЎОЉОЋОЉ ОъОАОЋОЎОъОф. ОЏОљОЕОе ОљОаОЋ ОцОЋОДОЊОЎОЮ ОбОю ОеОЌОцОЪ ОюОћОњОЎОб ОюОњОЋОЉОћ ОъОАОЋОЎОЮ РђЊ ОќОЋОћОЎ ОфОњОЋОЉОф ОъОЊОеОњОћ ОњОЮ ОЏОЪ. ОћОфОњОЋОЉОћ ОЕОю ОћОъОбОеОЏОф ОюОЏОаОЎОАОћ ОЏОќОЋ ОаОДОеОљОф ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОъОбОеОЏОф. ОЎОЕ ОюОЕОЎОЮ ОюОЉ ОЕОћОъОЊОеОњОћ ОЎОЏОЋОюОћ ОюОћОЋОцОЎОб ОњОЮ ОЏОћОцОеОбОћ, ОЋОюОљ ОеОД ОЏОљОЋОф ОЎОЎОЌОЋОА. ОљОЮ ОюОЊОЋОњОъОћ ОаОаОАОћ ОюОћОўОЎОА ОеОЌОцОЪ ОЋОфОфОЌОЎОю ОеОЋОЌ ОДОЉОЋОбОћ ОЕОъОАОЎОўОћ ОљОЋОфОЋ ОъОъОАОюОЋОюОЋ, ОќОЋ ОфОћОЎОћ ОЏОаОЎОАОф ОъОЊОеОњОћ ОЕОю ОћОцОеОбОћ.
ОљОБ ОбОю ОцОЎ ОЕОЊОеОЎОЕОЋОф ОъОъОбОеОЏОф ОЉОДОеОћ ОЎОЏОЋОюОЋОф ОюОћОЎОаОфОЪ ОЉОъОАОцОе ОЊОеОЏОЎОЮ, ОЏОњОЋОЪ ОЉОъОЎОЕОЋОе ОћОќОъОЪ ОљОЋ ОћОфОЊОе, ОюОЊОеОЎОЕОЋОф ОЉОъОЎОЕОЋОе ОћОќОъОЪ ОЎОЕОаОЋ ОцОЪ ОЎОЋОфОе ОљОЎОаОўОЋОљОЎОўОЎОЉОЎ, ОъОЕОЋОЮ ОЕОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОДОю ОЎОЋОфОе ОюОеОљОЋОф ОљОф ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЉОќОъОЪ, ОЋОЉОъОДОеОћ ОЕОю ОфОњОЋОЉОф ОъОЊОеОњОћ ОћОЊОеОЎОЕОЋОф ОЉОЊОеОџ ОЏОюОю ОЎОЎОаОфОаОЋ ОЉОъОЎОЕОЋОе ОћОќОъОЪ, ОЏОюОЋОъОе РђЊ ОћОЊОеОЎОЕОЋОф ОЎОЉОЋОўОљОЋ ОЏОЊОеОЎОЕОћ ОюОћОфОаОћОњОЋОф ОъОАОЋОЎОъОф ОЕОю ОћОъОбОеОЏОф ОЉОфОњОЋОЉОћ ОюОЏОаОЎОАОћ ОъОАОЋОЎОъОф. ОбОЉОЋОе ОфОњОЋОЉОф ОъОЊОеОњОћ ОЎОЕОаОЮ ОцОеОъОўОеОЎОЮ ОеОЉОЎОЮ ОЕОаОЎОфОЪ ОюОћОдОЉОЎОб ОбОюОЎОћОЮ, ОљОЋОюОЮ ОљОюОЋ ОћОъОЋОцОЎОбОЎОЮ ОЉОЊОеОџ ОЏОюОю ОЉОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф ОћОЮ[7]:
- ОќОъОЪ ОбОюОЎОћ (rise time): ОћОќОъОЪ ОЕОюОЋОДОЌ ОюОъОбОеОЏОф ОюОћОњОЎОб ОъОљОЌОЋОќ ОъОАОЋОЎОЮ ОЕОю ОбОеОџ ОћОЎОдОЎОљОћ ОћОАОЋОцОЎ ОюОљОЌОЋОќ ОљОЌОе. ОћОљОЌОЋОќ ОЉОЋ ОъОбОЋОаОЎОЎОаОЎОЮ ОЎОЏОЋОю ОюОћОЕОфОаОЋОф ОЏОфОюОЋОф ОЉОАОЋОњ ОћОъОбОеОЏОф ОЋОЉОЊОеОЎОЕОЋОф ОћОъОЕОфОъОЕ.
- ОфОњОЋОЉОф ОЎОфОе (overshoot): ОћОбОеОџ ОћОъОДОАОЎОъОюОЎ ОљОюОЎОЋ ОъОњОЎОбОћ ОћОъОбОеОЏОф ОЉОфОњОЋОЉОћ ОюОЏОаОЎОАОф ОъОЊОеОњОћ. ОюОеОЋОЉ ОъОЉОЋОўОљ ОЏОљОЌОЋОќ ОћОаОЋОАОБ ОюОбОеОџ ОћОАОЋОцОЎ ОљОюОЎОЋ ОъОњОЎОбОћ ОћОъОбОеОЏОф. ОюОЊОЋОњОъОћ, ОбОЉОЋОе ОъОбОеОЏОф ОЕОъОфОЎОЎОдОЉОф ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОбОю ОћОбОеОџ 1, ОћОњОбОћ ОюОбОеОџ ОъОДОАОЎОъОюОЎ ОЕОю ОЏ-1.4 ОъОЕОъОбОЋОфОћ ОфОњОЋОЉОф ОЎОфОе ОЕОю ОЏ-40%.
- ОќОъОЪ ОеОњОЎОбОћ (settling time): ОћОќОъОЪ ОЕОюОЋОДОЌ ОюОъОбОеОЏОф ОюОћОфОЏОаОА ОюОљОЌОЋОќ ОъОАОЋОЎОЮ ОъОбОеОЏОћ ОћОАОЋОцОЎ, ОЏОюОЋОъОе РђЊ ОюОћОњОЎОб ОюОъОдОЉ ОЉОЋ ОћОЎОљ ОюОљ ОЌОЋОеОњОф ОъОљОЌОЋОќ ОЕОњОЎОљОћ ОъОАОЋОЎОЮ. ОљОЌОЋОќ ОћОЕОњОЎОљОћ ОаОЎОфОЪ ОюОЕОЎОаОЋОЎ, ОЋОЎОЕ ОдОЋОеОџ ОюОдОЎОЎОЪ ОЉОљОЎОќОћ ОљОЌОЋОќ ОЕОњОЎОљОћ ОъОЊОЋОЉОе. ОюОЊОЋОњОъОћ, ОбОЉОЋОе ОъОбОеОЏОф ОћОъОфОЎОЎОдОЉОф ОбОю ОћОбОеОџ 1, ОќОъОЪ ОеОњОЎОбОћ ОбОЉОЋОе ОЕОњОЎОљОћ ОЕОю 2% ОЎОћОЎОћ ОћОќОъОЪ ОљОЕОе ОъОъОаОЋ ОЋОћОюОљОћ ОћОъОбОеОЏОф ОфОЎОЕОљОе ОЉОфОЌОЋОЮ (0.98, 1.02).
- ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ (steady state error): ОќОћОЋ ОћОъОеОЌОД ОЉОЎОЪ ОћОбОеОџ ОћОеОдОЋОЎ ОюОЉОЎОЪ ОћОбОеОџ ОљОюОЎОЋ ОфОњОЎОб ОћОЎОдОЎОљОћ ОюОљОЌОе ОќОъОЪ ОеОЉ. ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ ОљОцОАОЎОф ОцОЎОеОЋОЕОћ ОЕОЎОдОЎОљОф ОћОъОбОеОЏОф ОћОЎОљ ОЉОЊОЎОЋОД ОќОЋ ОЕОљОаОЋ ОеОЋОдОЎОЮ. ОъОўОеОф ОъОбОеОЏОф ОЉОДОеОћ, ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе, ОћОЎОљ ОћОДОўОаОф ОЕОњОЎОљОћ ОќОЋ ОбОЊ ОЏОъОћ ОЕОљОцОЕОе.
ОЎОдОЎОЉОЋОф
ОћОъОЋОЕОњ "ОЎОдОЎОЉОЋОф" ОаОъОдОљ ОЉОЕОЎОъОЋОЕ ОеОЉ ОЉОфОЌОЋОЮ ОћОћОаОЊОАОћ ОЋОћОъОЊОбОЎОЮ, ОЋОбОЕОЋОЎ ОюОЕОъОЕ ОЉОъОЋОЉОаОЎОЮ ОЕОЋОаОЎОЮ, ОЕОюОеОЋОЉ ОДОЕОЋОеОЎОЮ ОќОћ ОюОќОћ. ОЏОЕОъОЊОЋОЉОе ОЉОъОбОеОЏОЋОф ОЊОЎОаОъОЎОЋОф, ОЎОдОЎОЉОЋОф ОћОъОбОеОЏОф ОћОЎОљ ОъОЊОЊ ОюОаОўОЎОЎОфОћ ОюОћОЎОЕОљОе ОЉОъОдОЉ ОћОаОфОЋОЪ / ОюОЌОќОЋОе ОюОъОдОЉ ОљОцОАОЎ[8], ОЋОћОЎОљ ОъОћОЋОЋОћ ОцОеОъОўОе ОЌОЕОЋОЉ ОъОљОЋОЊ ОЉОфОЏОаОЋОЪ ОъОбОеОЏОЋОф ОЉОДОеОћ. ОаОЎОфОЪ ОюОдОЎОЎОЪ ОЕОфОЎ ОћОњОЊОеОЋОф ОюОЎОдОЎОЉОЋОф:
- ОЎОдОЎОЉОЋОф ОљОАОЎОъОцОўОЋОўОЎОф: ОъОбОеОЏОф ОЎОдОЎОЉОћ ОљОАОЎОъОцОўОЋОўОЎОф ОљОЮ ОбОЉОЋОе ОЏОю ОфОаОљОЎ ОћОфОЌОюОћ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОЕОљОБ Ою-0.
- ОЎОдОЎОЉОЋОф BIBO (Bounded Input Bounded Output)(ОљОа'): ОбОЉОЋОе ОфОаОљОЎ ОћОфОЌОюОћ ОљОцОАОЎ ОЋОЏОаОЎОАОћ ОЌОАОЋОъОћ ОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОћОЎОћ ОЌОАОЋОъОћ.
ОЏОЊОЋОњ' ОюОъОдОЉ ОЎОдОЎОЉ ОаОћОЋОњ ОюОћОЉОЎОљ ОЊОЋОњОъОћ ОЕОю ОЏОЊОЋОе ОћОъОЋОаОЌ ОЉОДОбОеОћ РђЊ ОЉОъОЎОЊОћ ОЋОЎОЕОаОЋ ОЌОЎОЏОЋОџ ОЏОюОЕОћОЋ ОЉОДОбОеОћ (ОъОћ ОЕОфОъОЎОЊ ОаОЏОЋОЪ ОбОЉОЋОе ОћОъОдОЎОљОЋОф ОЕОюОаОЋ), ОЏОю ОфОќОЋОќОћ ОЕОю ОћОЏОЊОЋОе ОфОАОфОЎОЎОЮ ОЉОъОдОЉ ОъОаОЋОЌОћ ОЉОфОЌОфОЎОф ОћОДОбОеОћ (ОљОюОљ ОљОЮ ОЏОЪ ОћОЋОљ ОЎОЎОЊОЌОБ ОћОЌОЋОдОћ). ОюОбОЋОъОф ОќОљОф, ОЏОЊОЋОе ОћОаОъОдОљ ОбОю ОњОЉОЎ ОДОбОеОћ ОћОцОЋОЏОћ ОаОъОдОљ ОЉОъОдОЉ ОюОљ ОЎОдОЎОЉ РђЊ ОЏОю ОћОцОеОбОћ ОДОўОаОћ ОфОњОеОЋОЮ ОюОЋ ОюОфОќОЋОќОћ ОљОЎОаОАОЋОцОЎОф. ОЎОЕОаОЋ ОЏОъОЋОЉОЪ ОњОЮ ОъОдОЉ ОЉОЎОаОЎОЎОЮ ОЉОЋ ОћОЏОЊОЋОе ОъОЋОаОЌ ОбОю ОЕОЋОюОЌОЪ ОЕОўОЋОЌ, ОЋОЉОъОДОеОћ ОЏОќОћ ОћОЏОЊОЋОе ОЎОЎОбОдОе ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе, ОљОЋОюОЮ ОюОљ ОЉОъОДОЋОъОЋ ОћОћОфОЌОюОфОЎ.
ОЉОфОЏОаОЋОЪ ОъОбОеОЏОф ОЉОДОеОћ, ОЏОъОбОў ОљОБ ОцОбОЮ ОљОЎОЪ ОбОЎОАОЋОД ОљОџ ОЋОеОД ОЉОЕОљОюОћ "ОћОљОЮ ОћОъОбОеОЏОф ОЎОдОЎОЉОћ?". ОћОЕОљОюОћ ОЕОЉОЊОеОџ ОЏОюОю ОаОЕОљОюОф ОћОЎОљ РђЊ "ОбОЊ ОЏОъОћ ОћОъОбОеОЏОф ОЎОдОЎОЉОћ", ОЏОюОЋОъОе РђЊ ОЉОъОЎОЊОћ ОЋОЎОфОеОЌОЕОЋ ОЕОЎОаОЋОЎОЎОЮ ОЉОюОфОЎ ОдОцОЋОЎОЎОЮ РђЊ ОљОЮ ОЉОъОбОеОЏОф ОЋОљОЮ ОЉОфОаОљОЎОЮ ОЉОћОЮ ОћОЎОљ ОдОеОЎОЏОћ ОюОцОбОЋОю РђЊ ОъОћОЋ ОъОеОЋОЋОЌ ОћОЉОЎОўОЌОЋОЪ ОЕОЎОЕ ОюОаОЋ ОюОцОаОЎ ОЕОћОъОбОеОЏОф ОфОљОЉОЊ ОЎОдОЎОЉОЋОф. ОЕОљОюОћ ОќОЋ ОЌОЕОЋОЉОћ ОъОЏОЎОЋОЋОЪ ОЕОДОЕОћ ОъОљОЋОЊ ОюОдОцОЋОф ОљОф ОъОЏОюОЋОю ОћОфОаОљОЎОЮ ОЕОЎОфОеОЌОЕОЋ ОЉОЕОЎОъОЋОЕ ОЉОъОбОеОЏОф ОЉОцОЋОбОю. ОЕОЎОаОЋОЎОЎОЮ ОЕОЏОљОюОЋ ОЎОЏОЋОюОЎОЮ ОюОћОЎОњОеОЮ ОъОћОъОбОеОЏОф ОбОдОъОћ, ОЏОњОЋОЪ ОЉОЕОЎОаОЋОЎОЎОЮ ОДОюОЎОЮ ОЉОЎОЪ ОцОеОЎОўОЎОЮ ОћОъОЎОЋОдОеОЎОЮ ОЉОцОАОЎ ОЎОЎОдОЋОе ОЕОЋОаОЎОЮ, ОљОЋ ОЕОЎОаОЋОЎ ОЏОюОЕОћОЋ ОЕОю ОћОъОбОеОЏОф ОюОљОЌОе ОЕОЎОъОЋОЕ / ОќОъОЪ ОъОъОЋОЕОџ ОЋОЏОЊОЋОъОћ, ОљОЋ ОЉОАОЉОЎОЉОћ ОЉОћ ОћОъОбОеОЏОф ОбОЋОЉОЊОф РђЊ ОЏОњОЋОЪ ОЕОЎОаОЋОЎОЎ ОўОъОцОеОўОЋОеОћ ОЉОюОфОЎ ОдОцОЋОЎОЎОЮ. ОЉОаОЋОАОБ, ОбОЋОЊОБ ОЎОдОЎОЉОЋОф ОаОЋОбОЊ ОюОћОДОўОЎОЪ ОљОф ОћОЕОцОбОф ОћОћОцОеОбОЋОф ОбОю ОћОъОбОеОЏОф РђЊ ОЉОЊОЋОњОъОф ОћОЏОЊОЋОе ОЉОДОбОеОћ, ОЏОЏОю ОЕОћОДОбОеОћ ОфОћОЎОћ ОфОюОЋОюОћ ОЎОЋОфОе, ОаОДОЉОю ОфОаОЋОЊОЋОф ОДОўОаОЋОф ОЎОЋОфОе ОбОЉОЋОе ОЊОЌОЎОцОћ ОќОћОћ ОЕОю ОћОЏОЊОЋОе.
ОбОЮ ОќОљОф, ОЎОдОЎОЉОЋОф ОњОЊОЋОюОћ ОъОЊОЎ ОњОЮ ОљОЎОаОћ ОўОЋОЉОћ, ОъОЕОЋОЮ ОЕОљОќ ОЎОћОЎОћ ОДОЕОћ ОюОЕОюОЋОў ОбОю ОћОъОбОеОЏОф РђЊ ОЏОъОЋ ОЕОфОњОЋОЉОф ОћОъОбОеОЏОф ОюОћОцОеОбОЋОф ОфОћОЎОћ ОДОўОаОћ, ОЏОџ ОњОЮ ОфОњОЋОЉОфОћ ОюОцОДОЋОЊОЋОф ОеОдОЋОЎОЋОф, ОЕОЏОЪ ОљОюОЋ ОћОЪ ОаОЎОАОЎОЋОаОЋОф ОюОћОЋОдОЎОљ ОљОЋОфОћ ОъОЕОЎОЋОЋОЎ ОъОЕОДОю. ОъОўОЋОА ОЎОдОЎОЉ ОъОЊОЎ, ОюОЊОЋОњОъОћ, ОюОљ ОЎОњОЎОЉ ОЉОдОЋОеОћ ОўОЋОЉОћ ОюОцОДОЋОЊОфОЎОЋ ОЕОю ОћОўОЎОЎОА ОЋОЎОДОЕОћ ОбОю ОћОЕОюОЎОўОћ ОЉОЋ.
ОћОЕОцОбОф ОЉОДОе PID ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЋОЎОдОЎОЉОЋОф ОћОъОбОеОЏОф
ОъОЏОЎОЋОЋОЪ ОЕОЏОю ОљОЌОЊ ОъОбОаОцОЎ ОЉОДОе PID ОъОЉОдОб ОцОбОЋОюОћ ОъОфОъОўОЎОф ОЕОЋОаОћ, ОћОЕОцОбОфОЋ ОЕОю ОЏОю ОбОаОБ ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОћОЎОљ ОљОЌОеОф. ОаОЎОфОЪ ОюОАОЏОЮ ОљОф ОћОЕОцОбОЋОф ОбОаОцОЎ ОћОЉОДОе ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе ОЉОўОЉОюОћ ОћОЉОљОћ[9], ОЏОљОЕОе ОћОћОЕОцОбОћ ОъОфОЎОЎОЌОАОф ОюОћОњОЊОюОф ОбОеОЏОЋ (ОЋОћОЕОцОбОфОЋ) ОЕОю ОћОбОаОБ:
| ОбОаОБ ОћОЉОДОе
|
ОћОЕОцОбОћ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе
|
| ОќОъОЪ ОбОюОЎОћ
|
ОфОњОЋОЉОф ОЎОфОе
|
ОќОъОЪ ОеОњОЎОбОћ
|
ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ
|
ОЎОдОЎОЉОЋОф
|
| ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ
( ) )
|
ОћОДОўОаОћ
|
ОћОњОЊОюОћ
|
ОћОЕОцОбОћ ОъОЋОбОўОћ
|
ОћОДОўОаОћ
|
ОфОюОЋОЎ ОъОбОеОЏОф
|
| ОљОЎОаОўОњОеОюОЎ
( ) )
|
ОћОДОўОаОћ
|
ОћОњОЊОюОћ
|
ОћОњОЊОюОћ
|
ОЉОЎОўОЋОю
|
ОћОДОўОаОћ
|
| ОЊОЎОцОеОаОдОЎОљОюОЎ
( ) )
|
ОћОЕОцОбОћ ОъОЋОбОўОћ
|
ОћОДОўОаОћ
|
ОћОДОўОаОћ
|
ОЌОАОе ОћОЕОцОбОћ
|
ОћОњОЊОюОћ ОбОЊ ОбОеОџ ОъОАОЋОЎОЮ
|
ОЌОЕОЋОЉ ОюОдОЎОЎОЪ ОЏОЎ ОъОЊОЋОЉОе ОЉОўОЉОюОћ ОЏОюОюОЎОф ОћОбОЋОАОДОф ОЉОъОбОеОЏОЋОф ОАОўОаОЊОеОўОЎОЋОф. ОћОћОЕОцОбОћ ОћОъОЊОЋОЎОДОф ОбОЕОЋОЎОћ ОюОћОЕОфОаОЋОф ОЏОфОюОЋОф ОЉОъОбОеОЏОф ОљОЋОфОћ ОљОаОЋ ОъОаОАОЎОЮ ОюОЉОДОе ОЋОЉОъОљОцОЎОЎОаОЎОћ (ОАОЊОе ОћОъОбОеОЏОф, ОћОЎОЋОфОћ ОъОЎОаОЎОъОЋОЮ ОцОљОќОћ ОЋОЏОЋ').
ОфОЎОљОЋОе ОъОфОъОўОЎ
ОъОЉОаОћ ОЏОюОюОЎ ОЕОю ОЉОДОе PID
ОћОдОЋОеОћ ОћОЏОюОюОЎОф ОЕОю ОЉОДОе PID ОъОфОЋОљОеОф ОбОю ОЎОЊОЎ ОћОцОЋОаОДОдОЎОћ:

ОЏОљОЕОе:
 ОћОЮ ОћОћОњОЉОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОљОЎОаОўОњОеОюОЎ ОЋОЊОЎОцОеОаОдОЎОљОюОЎ ОЉОћОфОљОъОћ, ОаОДОЉОбОЎОЮ ОбОю ОЎОЊОЎ ОћОъОфОЏОаОЪ ОљОЋ ОћОъОЕОфОъОЕ ОЋОДОЋОЉОбОЎОЮ ОљОф ОъОЎОЊОф ОћОЕОцОбОфОЋ ОЕОю ОЏОю ОбОаОБ ОЕОю ОћОЉОДОе (ОюОбОЎОфОЎОЮ ОъОАОЋОъОаОЎОЮ ОДОЉОЋОбОЎОЮ ОљОюОЋ ОЏ-
ОћОЮ ОћОћОњОЉОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ, ОљОЎОаОўОњОеОюОЎ ОЋОЊОЎОцОеОаОдОЎОљОюОЎ ОЉОћОфОљОъОћ, ОаОДОЉОбОЎОЮ ОбОю ОЎОЊОЎ ОћОъОфОЏОаОЪ ОљОЋ ОћОъОЕОфОъОЕ ОЋОДОЋОЉОбОЎОЮ ОљОф ОъОЎОЊОф ОћОЕОцОбОфОЋ ОЕОю ОЏОю ОбОаОБ ОЕОю ОћОЉОДОе (ОюОбОЎОфОЎОЮ ОъОАОЋОъОаОЎОЮ ОДОЉОЋОбОЎОЮ ОљОюОЋ ОЏ- ОЉОћОфОљОъОћ).
ОЉОћОфОљОъОћ). ОћОЋОљ ОљОЋОф ОћОЕОњОЎОљОћ ОћОаОЏОаОА ОюОЉОДОе,
ОћОЋОљ ОљОЋОф ОћОЕОњОЎОљОћ ОћОаОЏОаОА ОюОЉОДОе, ОћОЋОљ ОљОЋОф ОћОЉОДОеОћ ОћОЎОЋОдОљ ОъОћОЉОДОе ОЋОаОЏОаОА ОюОфОћОюОЎОџ.
ОћОЋОљ ОљОЋОф ОћОЉОДОеОћ ОћОЎОЋОдОљ ОъОћОЉОДОе ОЋОаОЏОаОА ОюОфОћОюОЎОџ. ОћОЋОљ ОъОЕОфОаОћ ОћОќОъОЪ.
ОћОЋОљ ОъОЕОфОаОћ ОћОќОъОЪ. ОћОЋОљ ОъОЕОфОаОћ ОћОљОЎОаОўОњОеОдОЎОћ.
ОћОЋОљ ОъОЕОфОаОћ ОћОљОЎОаОўОњОеОдОЎОћ.
ОћОдОњОћ ОаОЋОАОцОф ОЕОю ОћОцОЋОаОДОдОЎОћ ОЉОћ ОаОбОЕОћ ОЕОЎОъОЋОЕ ОъОфОДОЉОю ОбОю ОЎОЊОЎ ОћОћОдОЉОћ  :
:

ОћОЎОфОеОЋОЪ ОЉОћОдОњОћ ОќОЋ ОЕОю ОћОъОЕОЋОЋОљОћ ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОюОцОеОъОўОеОЎОЮ  ОЎОЕОаОћ ОъОЕОъОбОЋОф ОцОЎОќОЎОДОюОЎОф ОЕОю ОЎОЌОЎОЊОЋОф ОќОъОЪ.
ОЎОЕОаОћ ОъОЕОъОбОЋОф ОцОЎОќОЎОДОюОЎОф ОЕОю ОЎОЌОЎОЊОЋОф ОќОъОЪ.
ОбОю ОЎОЊОЎ ОЉОЎОдОЋОб ОћОфОъОеОф ОюОцОюОА ОбОю ОћОцОЋОаОДОдОЎОћ (ОЉОдОЋОеОфОћ ОћОеОљОЕОЋОаОћ ОЕОћОЋОЉОљОћ ОюОбОЎОю) ОъОфОДОЉОюОф ОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф ОЕОю ОћОЉОДОе:

ОцОЋОаОДОдОЎОћ ОќОЋ ОЌОЕОЋОЉОћ ОъОљОЋОЊ ОъОЏОЎОЋОЋОЪ ОЕОЉОфОЌОЋОЮ ОћОЉОДОеОћ ОбОЎОДОе ОћОфОЏОаОЋОЪ ОаОбОЕОћ ОЉОъОЎОЕОЋОе Оћ-s ОЋОюОљ ОЉОъОЎОЕОЋОе ОћОќОъОЪ.
ОЌОЕОЋОЉ ОюОдОЎОЎОЪ ОЏОЎ ОдОЋОеОфОЋ ОћОцОЕОЋОўОћ ОЕОю ОЉОДОе PID ОаОЋОЕОљОф ОбОЎОъОћ ОЏОъОћ ОЉОбОЎОЋОф, ОЋОюОЏОЪ ОЉОъОДОеОЎОЮ ОеОЉОЎОЮ ОаОбОЕОЎОЮ ОЕОЎОаОЋОЎОЎОЮ ОДОюОЎОЮ ОЉОЉОДОе ОбОю ОъОаОф ОюОцОфОЋОе ОЉОбОЎОЋОф ОљОюОЋ, ОћОъОфОЉОўОљОЎОЮ ОЏОъОЋОЉОЪ ОњОЮ ОЉОцОЋОаОДОдОЎОЋОф ОћОъОфОљОеОЋОф ОљОф ОцОбОЋОюОфОЋ. ОбОЮ ОќОљОф, ОЕОЎОаОЋОЎОЎОЮ ОљОюОЋ ОљОЎОаОЮ ОъОЕОаОЎОЮ ОљОф ОљОЋОцОЪ ОцОбОЋОюОфОЋ ОћОбОДОеОЋОаОЎОф, ОЋОаОЋОбОЊОЋ ОюОцОфОЋОе ОЉОбОЎОЋОф ОћОъОфОеОЌОЕОЋОф ОЉОЕОю ОАОЎОЉОЋОф ОЕОљОЎОаОЪ ОЌОюОД ОъОЌОЋОњ ОћОЉОДОеОћ ОћОљОЎОЊОЎОљОюОЎ, ОЏОњОЋОЪ ОеОбОЕОЎ ОъОЊОЎОЊОћ ОЋОфОЋОцОбОЋОф ОцОЎОќОЎОДОюОЎОЋОф ОЌОеОЎОњОЋОф.
ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ
 ОћОЕОцОбОф ОћОбОаОБ ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОЕОцОбОф ОћОбОаОБ ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОцОбОЋОюОћ ОћОъОфОъОўОЎОф ОћОъОфОЉОдОбОф ОбОю ОЎОЊОЎ ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОаОфОЋОаОћ Об"ОЎ:

ОЌОюОД ОќОћ ОЕОю ОћОЉОДОе ОъОДОЉОю ОљОф ОбОеОЏОћ ОћОаОЋОЏОЌОЎ ОЕОю ОћОЕОњОЎОљОћ, ОЋОъОЏОцОЎОю ОљОЋОфОЋ ОЉОДОЉОЋОб  . ОќОћОЋ "ОћОћОњОЉОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ" ОЕОю ОћОЉОДОе, ОЋОћОЋОљ ОЌОюОДОЋ ОћОцОЕОЋОў ОЉОЎОЋОфОе ОЕОю ОћОЉОДОе. ОЏОЏОю ОЕОбОеОџ ОћОЕОњОЎОљОћ ОЎОћОЎОћ ОњОЊОЋОю ОЎОЋОфОе, ОЏОџ ОЎОњОЊОю ОбОеОџ ОћОљОЋОф ОћОЎОЋОдОљ ОъОЪ ОћОЉОДОе ОЋОаОЏОаОА ОюОфОћОюОЎОџ. ОЎОфОеОЋОаОЋОфОЎОЋ ОЕОю ОћОњОЊОюОф ОћОцОеОъОўОе
. ОќОћОЋ "ОћОћОњОЉОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ" ОЕОю ОћОЉОДОе, ОЋОћОЋОљ ОЌОюОДОЋ ОћОцОЕОЋОў ОЉОЎОЋОфОе ОЕОю ОћОЉОДОе. ОЏОЏОю ОЕОбОеОџ ОћОЕОњОЎОљОћ ОЎОћОЎОћ ОњОЊОЋОю ОЎОЋОфОе, ОЏОџ ОЎОњОЊОю ОбОеОџ ОћОљОЋОф ОћОЎОЋОдОљ ОъОЪ ОћОЉОДОе ОЋОаОЏОаОА ОюОфОћОюОЎОџ. ОЎОфОеОЋОаОЋОфОЎОЋ ОЕОю ОћОњОЊОюОф ОћОцОеОъОўОе  ОћОЪ ОбОДОЎОЉОћ ОўОЋОЉОћ ОЎОЋОфОе ОЕОю ОЎОдОЎОљОф ОћОъОбОеОЏОф ОљОЌОе ОљОЋОф ОћОЎОЎОЌОЋОА (ОЕОњОЎОљОћ ОДОўОаОћ ОЎОЋОфОе), ОћОДОўОаОф ОќОъОЪ ОћОфОњОЋОЉОћ ОЕОю ОћОъОбОеОЏОф ОюОцОДОЋОЊОЋОф. ОбОЮ ОќОљОф, ОћОњОЊОюОћ ОЕОю ОцОеОъОўОе ОќОћ ОъОДОўОЎОаОћ ОљОф ОеОЎОАОЋОЪ ОћОъОбОеОЏОф ОЋОљОБ ОбОюОЋОюОћ ОюОћОЉОЎОљ ОюОљОЎ-ОЎОдОЎОЉОЋОф.
ОћОЪ ОбОДОЎОЉОћ ОўОЋОЉОћ ОЎОЋОфОе ОЕОю ОЎОдОЎОљОф ОћОъОбОеОЏОф ОљОЌОе ОљОЋОф ОћОЎОЎОЌОЋОА (ОЕОњОЎОљОћ ОДОўОаОћ ОЎОЋОфОе), ОћОДОўОаОф ОќОъОЪ ОћОфОњОЋОЉОћ ОЕОю ОћОъОбОеОЏОф ОюОцОДОЋОЊОЋОф. ОбОЮ ОќОљОф, ОћОњОЊОюОћ ОЕОю ОцОеОъОўОе ОќОћ ОъОДОўОЎОаОћ ОљОф ОеОЎОАОЋОЪ ОћОъОбОеОЏОф ОЋОљОБ ОбОюОЋОюОћ ОюОћОЉОЎОљ ОюОљОЎ-ОЎОдОЎОЉОЋОф.
ОЕОЎОъОЋОЕ ОЉОбОаОБ ОћОќОћ ОЉОюОЉОЊ ОъОЕОъОбОЋОфОЋ, ОЉОцОЋОбОю, ОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ. ОћОЌОАОеОЋОЪ ОћОъОЕОъОбОЋОфОЎ ОЉОЎОЋОфОе ОЕОю ОћОЉОДОе ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОбОЉОЋОе ОЏОаОЎОАОф ОъОЊОеОњОћ, ОћОаОцОЋОдОћ ОъОљОЋОЊ ОЉОъОбОеОЏОЋОф ОЉОДОеОћ, ОфОфОДОЉОю ОЉОћОЏОеОЌ ОЕОњОЎОљОф ОъОдОЉ ОъОфОъОЎОЊ, ОЏОюОЋОъОе РђЊ ОћОЉОДОе ОюОљ ОЎОдОюОЎОЌ ОюОћОЉОЎОљ ОљОф ОЎОдОЎОљОф ОћОъОбОеОЏОф ОюОбОеОЏОћ ОћОеОдОЋОЎ ОњОЮ ОюОљОЌОе ОќОъОЪ ОеОЉ. ОЊОЉОе ОќОћ ОаОЋОЉОб ОъОЏОџ ОЕОЉОЕОю ОћОДОЕОе ОћОЎОЕОЎОе ОЉОЎОЪ ОћОЕОаОЎОЎОЮ, ОЕОњОЎОљОћ ОљОцОАОЎОф (ОъОдОЉ ОЉОЋ ОћОЎОдОЎОљОћ ОЉОцОЋОбОю ОЕОЋОЋОћ ОюОЎОдОЎОљОћ ОћОеОдОЋОЎОћ) ОфОњОеОЋОЮ ОЉОћОЏОеОЌ ОюОљОЋОф ОЉОДОеОћ ОљОцОА, ОЏОюОЋОъОе, ОћОфОћОюОЎОџ ОЏОюОю ОюОљ ОЎОДОЉОю ОцОДОЋОЊОћ, ОЋОюОЏОЪ ОЎОфОЌОЎОю ОюОАОўОЋОф ОъОбОеОџ ОћОЎОдОЎОљОћ ОћОЊОеОЋОЕ. ОюОЕОЮ ОЊОЋОњОъОћ ОаОЎОфОЪ ОюОДОЌОф ОфОаОЋОе ОћОъОЉОЋОДОе ОбОю ОЎОЊОЎ ОЉОДОе ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ РђЊ ОъОЏОЎОЋОЋОЪ ОЕОћОфОаОЋОе ОфОъОЎОЊ ОъОљОЉОЊ ОЌОЋОЮ ОюОАОЉОЎОЉОћ, ОЉОъОЎОЊОћ ОЋОћОфОаОЋОе ОаОъОдОљ ОЉОЊОЎОЋОД ОЉОўОъОцОеОўОЋОеОћ ОћОЊОеОЋОЕОћ ОъОъОаОЋ, ОЎОњОеОЋОЮ ОћОЉОДОе ОюОћОцОАОДОф ОћОќОеОЮ, ОЋОўОъОцОеОўОЋОеОф ОћОфОаОЋОе ОфОеОЊ ОбОЊ ОюОћОцОбОюОћ ОъОЌОЋОЊОЕОф, ОЋОЌОЋОќОе ОЌОюОЎОюОћ. ОћОфОћОюОЎОџ ОћОЎОЌОЎОЊ ОЕОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОфОфОљОцОА ОЉОЋ ОЎОћОЎОћ ОфОћОюОЎОџ ОћОЏОЋОюОю ОљОЎОаОўОњОеОўОЋОе.
ОћОЌОюОД ОћОљОЎОаОўОњОеОюОЎ
 ОћОЕОцОбОф ОћОбОаОБ ОћОљОЎОаОўОњОеОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОЕОцОбОф ОћОбОаОБ ОћОљОЎОаОўОњОеОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОцОбОЋОюОћ ОћОъОфОъОўОЎОф ОћОъОЉОЋОдОбОф ОбОю ОЎОЊОЎ ОћОЌОюОД ОћОљОЎОаОўОњОеОюОЎ ОаОфОЋОаОћ Об"ОЎ:

ОЌОюОД ОќОћ ОЕОю ОћОЉОДОе ОъОЉОдОб ОљОЎОаОўОњОеОдОЎОћ ОЉОќОъОЪ ОЕОю ОћОЕОњОЎОљОћ ОъОфОЌОЎОюОф ОћОъОЊОЎОЊОћ ОЋОбОЊ ОеОњОб ОћОЌОЎОЕОЋОЉ, ОЋОъОЏОцОЎОю ОљОф ОћОфОЋОдОљОћ ОЉОДОЉОЋОб  . ОЏОЏОю ОЕОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОћОЎОћ ОеОЌОЋОДОћ ОЎОЋОфОе ОъОћОбОеОџ ОћОеОдОЋОЎ, ОЋОЏОЏОю ОЕОЎОфОљОеОџ ОћОќОъОЪ ОЉОЋ ОъОдОЉ ОќОћ ОЎОЎОъОЕОџ, ОфОњОЊОю ОћОЕОцОбОфОЋ ОЕОю ОћОЌОюОД ОћОљОЎОаОўОњОеОюОЎ ОбОю ОћОЉОДОе.
. ОЏОЏОю ОЕОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОћОЎОћ ОеОЌОЋОДОћ ОЎОЋОфОе ОъОћОбОеОџ ОћОеОдОЋОЎ, ОЋОЏОЏОю ОЕОЎОфОљОеОџ ОћОќОъОЪ ОЉОЋ ОъОдОЉ ОќОћ ОЎОЎОъОЕОџ, ОфОњОЊОю ОћОЕОцОбОфОЋ ОЕОю ОћОЌОюОД ОћОљОЎОаОўОњОеОюОЎ ОбОю ОћОЉОДОе.
ОћОЕОЎОаОЋОЎ ОћОъОЕОъОбОЋОфОЎ ОЕОаОбОЕОћ ОЉОъОбОеОЏОф ОЉОбОДОЉОЋОф ОћОЋОАОцОф ОЌОюОД ОќОћ ОЕОю ОћОЉОДОе ОћОЋОљ ОфОЋОАОцОф ОДОЋОўОЉ ОЉОеОљОЕОЎОф (ОљОЎОаОўОњОеОўОЋОе) ОюОЌОЋОњ ОћОцОфОЋОЌ, ОЏОюОЋОъОе РђЊ ОћОњОЊОюОф ОАОЋОњ ОћОъОбОеОЏОф (ОАОЋОњ ОћОъОбОеОЏОф ОъОЋОњОЊОе ОбОю ОЎОЊОЎ ОъОАОцОе ОћОљОЎОаОўОњОеОўОЋОеОЎОЮ ОЕОю ОћОЌОЋОњ ОћОцОфОЋОЌ, ОЋОъОЕОфОаОћ ОЏОфОюОЋОф ОЉОЏОаОЎОАОћ ОљОюОЎОћ ОљОаОЋ ОъОфОЎОЎОЌОАОЎОЮ. ОЉОљОЋОцОЪ ОЏОюОюОЎ ОаОЎОфОЪ ОюОЋОъОе ОЕОЏОЏОю ОЕОАОЋОњ ОћОъОбОеОЏОф ОњОЊОЋОю ОЎОЋОфОе, ОЎОЏОЋОюОф ОћОДОўОаОф ОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОўОЋОЉОћ ОЎОЋОфОе). ОфОЋОАОцОф ОќОћ ОъОЕОъОбОЋОфОћ ОљОЎОцОЋОА ОЕОњОЎОљОф ОћОъОдОЉ ОћОъОфОъОЎОЊ ОбОЉОЋОе ОЏОаОЎОАОф ОъОЊОеОњОћ, ОЏОюОЋОъОе РђЊ ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе (ОЏОфОюОЋОф ОЉОфОћОюОЎОџ ОћОъОЉОЋОДОе ОЋОЉОбОеОЏОЎ ОћОДОЉОЋОбОЎОЮ ОЕОю ОћОЉОДОе), ОЎОдОЎОљОф ОћОъОбОеОЏОф ОфОћОЎОћ ОЕОЋОЋОћ ОЉОЊОЎОЋОД ОюОЎОдОЎОљОћ ОЉОћ ОљОаОЋ ОъОбОЋОаОЎОЎОаОЎОЮ. ОюОеОЋОЉ ОќОЋ ОфОћОЎОћ ОъОўОеОф ОћОЋОАОцОф ОЌОюОД ОќОћ ОЕОю ОћОЉОДОе.
ОЌОАОеОЋОаОЋ ОЕОю ОЌОюОД ОќОћ ОаОЋОЉОбОф ОъОћОбОЋОЉОЊОћ ОЕОћОЋОАОцОф ОДОЋОўОЉ ОЉОеОљОЕОЎОф ОъОЋОАОЎОцОћ ОюОЌОЋОњ ОћОцОфОЋОЌ ОцОЎОњОЋОе ОцОљОќОћ ОЕОю ОЏ- , ОЋОЉОЏОџ ОъОДОўОЎОаОЎОЮ ОљОф ОбОЋОЊОБ ОћОцОљОќОћ ОЋОљОф ОЎОдОЎОЉОЋОф ОћОъОбОеОЏОф. ОЉОъОЎОЊОћ ОЋОћОъОбОеОЏОф ОъОљОЉОЊОф ОЎОдОЎОЉОЋОф ОбОДОЉ ОћОЋОАОцОф ОЌОюОД ОќОћ, ОЎОЎОфОЏОЪ ОЋОЎОћОЎОћ ОдОЋОеОџ ОюОћОЋОАОЎОБ ОљОф ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОбОю ОъОаОф ОюОцОдОЋОф ОбОю ОЏОџ.
, ОЋОЉОЏОџ ОъОДОўОЎОаОЎОЮ ОљОф ОбОЋОЊОБ ОћОцОљОќОћ ОЋОљОф ОЎОдОЎОЉОЋОф ОћОъОбОеОЏОф. ОЉОъОЎОЊОћ ОЋОћОъОбОеОЏОф ОъОљОЉОЊОф ОЎОдОЎОЉОЋОф ОбОДОЉ ОћОЋОАОцОф ОЌОюОД ОќОћ, ОЎОЎОфОЏОЪ ОЋОЎОћОЎОћ ОдОЋОеОџ ОюОћОЋОАОЎОБ ОљОф ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОбОю ОъОаОф ОюОцОдОЋОф ОбОю ОЏОџ.
ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ
 ОћОЕОцОбОф ОћОбОаОБ ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОЕОцОбОф ОћОбОаОБ ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОбОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ ОЕОю ОћОЌОЋОњ ОћОАОњОЋОе.
ОћОцОбОЋОюОћ ОћОъОфОъОўОЎОф ОћОъОЉОЋОдОбОф ОбОю ОЎОЊОЎ ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОаОфОЋОаОћ Об"ОЎ:

ОЌОюОД ОќОћ ОЕОю ОћОЉОДОе ОюОљ ОъОфОЎОЎОЌОА ОюОбОеОџ ОћОЕОњОЎОљОћ, ОљОюОљ ОюОДОдОЉ ОћОЕОЎОаОЋОЎ ОЕОюОЋ. ОЏОюОЋОъОе, ОЌОюОД ОќОћ ОъОаОАОћ "ОюОдОцОЋОф" ОљОф ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЉОћОЎОаОфОЪ ОДОдОЉ ОћОДОўОаОф ОћОЕОњОЎОљОћ ОћОаОЋОЏОЌОЎ, ОЋОЉОЏОџ ОюОћОЉОЎОљ ОюОЉОЎОдОЋОбОЎОЮ ОўОЋОЉОЎОЮ ОЎОЋОфОе ОЏОъОЋ ОќОъОЪ ОеОњОЎОбОћ ОДОўОЪ ОЎОЋОфОе ОЋОЎОдОЎОЉОЋОф ОњОЊОЋОюОћ ОЎОЋОфОе ОЕОю ОћОъОбОеОЏОф, ОЋОЉОЏОџ ОюОљОцОЕОе ОњОЮ ОљОф ОћОњОЉОеОф ОћОЌОюОД ОћОцОеОЋОцОЋОеОдОЎОЋОаОюОЎ. ОбОЉОЋОе ОЏОаОЎОАОф ОъОЊОеОњОћ ОаОЎОфОЪ ОюОеОљОЋОф ОќОљОф ОбОю ОЎОЊОЎ ОћОњОЊОеОф ОљОЋОф ОћОЕОњОЎОљОћ:

ОъОЏОЎОЋОЋОЪ ОЕОљОЋОф ОћОЏОаОЎОАОћ ОДОЉОЋОб ОЉОќОъОЪ (ОъОЊОеОњОћ), ОаОњОќОеОфОЋ ОъОфОљОцОАОф. ОаОЎОфОЪ ОюОеОљОЋОф ОъОЏОљОЪ ОЕОДОдОЉ ОЕОЎОаОЋОЎ ОћОЎОдОЎОљОћ ОаОъОдОљ ОЉОАОЎОъОЪ ОћОцОЋОџ ОюОДОдОЉ ОЕОЎОаОЋОЎ ОћОЕОњОЎОљОћ, ОЋОюОЏОЪ ОЌОюОД ОќОћ ОъОћОЋОЋОћ ОЉОбОдОЮ ОъОЕОЋОЉ ОЕОюОЎОюОЎ ОбОЉОЋОе ОћОЎОдОЎОљОћ РђЊ ОЏОљОЕОе ОћОЎОдОЎОљОћ ОъОЕОфОаОћ ОЉОъОћОЎОеОЋОф (ОћОъОбОеОЏОф ОъОфОДОеОЉОф ОЉОъОћОЎОеОЋОф ОюОбОеОџ ОћОеОдОЋОЎ), ОљОЋОф ОћОЕОњОЎОљОћ ОъОЕОфОаОћ ОъОћОе, ОЋОЉОЕОю ОћОАОЎОъОЪ ОћОћОцОЋОџ ОъОДОўОЎОЪ ОљОф ОљОЋОф ОћОЉОДОеОћ ОЋОъОъОфОЪ ОљОф ОћОЕОЎОаОЋОЎ ОЉОЎОдОЎОљОћ, ОЋОЉОЏОџ ОъОеОАОЪ ОљОф ОфОњОЋОЉОф ОћОъОбОеОЏОф. ОаОЎОфОЪ ОюОћОЉОЎОљ ОЏОЊОЋОњОъОћ ОъОдОЉ ОЉОЋ ОљОаОЋ ОъОбОЋОаОЎОЎОаОЎОЮ ОюОћОњОЎОб ОюОъОЎОДОЋОЮ ОъОАОЋОЎОЮ ОбОЮ ОъОЏОЋОаОЎОф ОъОъОдОЉ ОъОаОЋОЌОћ. ОЉОъОЎОЊОћ ОЋОаОюОЌОЦ ОбОю ОћОЊОЋОЋОЕОћ ОЌОќОД ОъОЊОЎ, ОљОъОаОЮ ОаОњОЎОб ОюОЎОбОЊ, ОљОЋОюОЮ ОљОаОЋ ОбОюОЋОюОЎОЮ ОњОЮ ОюОбОЉОЋОе ОљОЋОфОЋ ОЉОъОЎОЊОћ ОЋОюОљ ОаОфОЌОЕОЉ ОЉОъОћОЎОеОЋОф ОЉОћ ОљОаОЋ ОъОфОДОеОЉОЎОЮ ОюОЎОбОЊ. ОћОЌОюОД ОћОЊОЎОцОеОаОдОЎОљОюОЎ ОъОфОЌОЕОЉ ОЉОЏОџ ОЋОЉОЋОЊОД ОЏОъОћ ОъОћОе ОљОаОЋ ОъОфОДОеОЉОЎОЮ ОюОљОЎОцОЋОА ОћОЕОњОЎОљОћ ОЋОъОњОЊОЎОю/ОъОДОўОЎОЪ ОљОф ОљОЋОф ОћОЉОДОеОћ ОЉОћОфОљОЮ, ОЋОЉОбОдОЮ ОаОЎОфОЪ ОюОЋОъОе ОЕОћОЋОљ ОдОЋОцОћ ОљОф ОбОеОџ ОћОЕОњОЎОљОћ ОћОбОфОЎОЊОЎ ОЋОцОЋОбОю ОюОъОаОЎОбОф ОфОњОЋОЉОф ОЎОфОе ОњОЊОЋОюОћ ОбОЋОЊ ОюОцОаОЎ ОЕОќОЋ ОъОфОцОфОЌОф..
ОъОЕОъОбОЋОф ОћОЕОцОбОф ОЌОюОД ОќОћ ОЉОфОЌОЋОЮ ОћОфОЊОе ОћОЎОљ ОћОЋОАОцОф ОљОцОА, ОЕОъОЕОъОбОЋОфОћ ОћОЎОљ ОћОЋОАОцОф ОцОљОќОћ ОюОЌОЋОњ ОћОцОфОЋОЌ, ОъОћ ОЕОћОЋОцОџ ОљОф ОћОъОбОеОЏОф ОюОЎОдОЎОЉОћ ОЎОЋОфОе.
ОЏо┤о╝ОЎОЋОЋОаОЋо╝ОЪ ОћОЉОДОе
ОћОфОћОюОЎОџ ОЉОЋ ОаОДОЉОб ОъОЉОаОћ ОћОЉОДОе ОЋОљОЋОцОЪ ОћОЕОцОбОфОЋ ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОбОю ОЎОЊОЎ ОћОъОЕОфОъОЕ ОаОДОеОљ "ОЏОЋОЋОаОЋОЪ ОћОЉОДОе". ОЏОцОЎ ОЕОфОЋОљОе, ОюОЉОДОе ОъОАОцОе ОбОаОцОЎОЮ ОЋОљОЋОцОаОЎ ОћОЕОцОбОћ ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф, ОЋОбОю ОћОъОЕОфОъОЕ ОюОДОЉОЋОб ОЏОЎОдОЊ ОЎОЕОцОЎОб ОћОЉОДОе ОбОю ОћОъОбОеОЏОф.
 ОюОљОЌОе ОфОЌОЎОюОф ОћОцОбОюОфОЋ ОЕОю ОўОюОАОДОЋОц ОћОЌОюОю ОћОљОЉОю, ОћОфОЉОеОе ОЏОЎ ОћОфОъОЋОаОЋОф ОљОЋОфОЪ ОћОЋОљ ОъОцОЎОД ОеОЌОЋОДОЋОф ОъОћОеОќОЋОюОЋОдОЎОћ ОюОћ ОдОЎОцОЋ. ОћОфОЉОеОе ОЏОЎ ОЊОЉОе ОќОћ ОаОЉОб ОбОДОЉ ОъОЏОЕОЎОе ОЉОЊОЎОДОћ ОЕОћОЋОеОЏОЉ ОЉОъОеОЌОД ОЕОю ОЏ-1.308 Оъ"Оъ ОъОћОъОДОЋОЮ ОћОЊОеОЋОЕ, ОфОДОюОћ ОЕОЊОеОЕОћ ОЕОюОЎОЌОћ ОЕОю ОљОАОўОеОЋОаОљОЋОўОЎОЮ ОюОЌОюОю ОюОЕОЮ ОћОфОДОаОф ОъОбОеОЏОф ОљОЋОцОўОЎОф ОаОЋОАОцОф ОЉОўОюОАОДОЋОц. ОќОЋОћОЎ ОЊОЋОњОъОћ ОЎОЊОЋОбОћ ОюОъОДОеОћ ОЉОЋ ОфОћОюОЎОџ ОЉОаОЎОЎОф ОћОъОбОеОЏОф ОюОљ ОфОљОЮ ОљОф ОћОЊОеОЎОЕОЋОф ОћОъОЌОъОЎОеОЋОф ОЉОћОЪ ОћОЎОћ ОљОъОЋОе ОюОбОъОЋОЊ. ОфОъОЋОаОћ ОќОЋ ОъОеОљОћ ОљОф ОћОЕОЎОцОЋОе ОЉОеОќОЋОюОЋОдОЎОЎОф ОћОфОъОЋОаОЋОф ОюОцОаОЎ ОћОфОЎОДОЋОЪ ОЋОюОљОЌОеОЎОЋ.
ОюОљОЌОе ОфОЌОЎОюОф ОћОцОбОюОфОЋ ОЕОю ОўОюОАОДОЋОц ОћОЌОюОю ОћОљОЉОю, ОћОфОЉОеОе ОЏОЎ ОћОфОъОЋОаОЋОф ОљОЋОфОЪ ОћОЋОљ ОъОцОЎОД ОеОЌОЋОДОЋОф ОъОћОеОќОЋОюОЋОдОЎОћ ОюОћ ОдОЎОцОЋ. ОћОфОЉОеОе ОЏОЎ ОЊОЉОе ОќОћ ОаОЉОб ОбОДОЉ ОъОЏОЕОЎОе ОЉОЊОЎОДОћ ОЕОћОЋОеОЏОЉ ОЉОъОеОЌОД ОЕОю ОЏ-1.308 Оъ"Оъ ОъОћОъОДОЋОЮ ОћОЊОеОЋОЕ, ОфОДОюОћ ОЕОЊОеОЕОћ ОЕОюОЎОЌОћ ОЕОю ОљОАОўОеОЋОаОљОЋОўОЎОЮ ОюОЌОюОю ОюОЕОЮ ОћОфОДОаОф ОъОбОеОЏОф ОљОЋОцОўОЎОф ОаОЋОАОцОф ОЉОўОюОАОДОЋОц. ОќОЋОћОЎ ОЊОЋОњОъОћ ОЎОЊОЋОбОћ ОюОъОДОеОћ ОЉОЋ ОфОћОюОЎОџ ОЉОаОЎОЎОф ОћОъОбОеОЏОф ОюОљ ОфОљОЮ ОљОф ОћОЊОеОЎОЕОЋОф ОћОъОЌОъОЎОеОЋОф ОЉОћОЪ ОћОЎОћ ОљОъОЋОе ОюОбОъОЋОЊ. ОфОъОЋОаОћ ОќОЋ ОъОеОљОћ ОљОф ОћОЕОЎОцОЋОе ОЉОеОќОЋОюОЋОдОЎОЎОф ОћОфОъОЋОаОЋОф ОюОцОаОЎ ОћОфОЎОДОЋОЪ ОЋОюОљОЌОеОЎОЋ.
ОЉОљОЋОцОЪ ОЏОюОюОЎ, ОЉОфОЏОаОЋОЪ ОъОбОеОЏОЋОф ОЉОДОеОћ (ОЋОъОбОеОЏОЋОф ОћОаОЊОАОЎОЋОф ОЉОљОЋОцОЪ ОЏОюОюОЎ[10]), ОћОЊОЉОе ОћОеОљОЕОЋОЪ ОЉОЋ ОбОЋОАОДОЎОЮ ОћОЋОљ ОћОЊОеОЎОЕОЋОф РђЊ ОљОЎОюОЋ ОъОўОеОЋОф ОћОъОбОеОЏОф ОљОъОЋОеОћ ОюОћОЕОЎОњ, ОЋОЏОЎОдОЊ ОбОюОЎОћ ОюОбОЕОЋОф ОќОљОф[11]. ОЉОЉОаОЎОЎОф ОъОЏОЋОаОЎОф, ОюОЊОЋОњОъОћ, ОљОаОЋ ОъОњОЊОЎОеОЎОЮ ОъОбОеОЏОф ОћОъОљОцОЕОеОф ОюОћОАОЎОб ОљОаОЕОЎОЮ ОљОЋ ОъОўОбОЪ ОъОъОДОЋОЮ ОюОъОДОЋОЮ, ОЋОљОаОЋ ОЎОЏОЋОюОЎОЮ ОюОЊОеОЋОЕ ОъОћОЎОеОЋОф ОъОДОАОЎОъОюОЎОф ОљОюОЎОћ ОћОЎОљ ОЎОЏОЋОюОћ ОюОћОњОЎОб. ОЏОъОЋОЉОЪ ОЕОюОъОбОеОЏОф ОбОЕОЋОЎОЋОф ОюОћОЎОЋОф ОЊОеОЎОЕОЋОф ОеОЉОЋОф ОъОфОЌОЋОъОЎОЮ ОЕОЋОаОЎОЮ РђЊ ОбОЉОЋОе ОћОъОЏОЋОаОЎОф, ОюОЊОЋОњОъОћ, ОаОЎОфОЪ ОюОћОњОЊОЎОе ОЎОЏОЋОюОф ОћОљОдОћ, ОЎОЏОЋОюОф ОЉОюОЎОъОћ, ОбОъОЎОЊОћ ОЉОъОЉОЌОаОЎ ОЉОўОЎОЌОЋОф ОЏОљОюОЋ ОЋОљОЌОеОЎОЮ, ОЋОбОЋОЊ. ОеОД ОЏОљОЕОе ОаОфОЋОаОЋОф ОћОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф ОаОЎОфОЪ ОюОћОфОЌОЎОю ОюОЊОЋОЪ ОЉОљОЋОцОЪ ОЉОЋ ОаОЎОфОЪ ОюОъОюОљ ОљОЋОфОЪ. ОбОЮ ОќОљОф, ОЉОъОбОеОЏОЋОф ОЌОЋОЉОЉОаОЎОЋОф, ОюОЊОЋОњОъОћ, ОћОЊОеОЎОЕОЋОф ОюОљ ОдОеОЎОЏОЋОф ОюОћОЎОЋОф ОъОЋОњОЊОеОЋОф ОћОЎОўОЉ РђЊ ОљОЮ ОаОЉОаОћ ОъОЏОЋОаОЎОф ОбОю ОЕОюОў ОЏОфОЌОЉОЎОЉ, ОЉОЊОеОџ ОЏОюОю ОюОљ ОаОЊОеОЋОЕ ОъОћОЎОеОЋОф ОъОАОЋОЎОъОф, ОЋОаОЉОаОћ ОЋОаОЕОцОе ОљОф ОћОъОбОеОЏОф ОбОЊ ОЕОаОњОЎОб ОюОфОЋОдОљОЋОф ОЕОљОаОЋ ОъОеОЋОдОЎОЮ ОъОћОЪ. ОћОЉОЊОю ОќОћ ОњОЮ ОЎОЕОцОЎОб ОбОю ОћОљОЋОцОЪ ОЉОЋ ОљОаОЋ ОъОфОЏОаОаОЎОЮ ОљОф ОћОъОбОеОЏОф ОЋОбОю ОћОЊОЎОЋОД ОћОаОЊОеОЕ ОЉОфОЏОаОЋОЪ ОЋОЉОЉОЎОдОЋОб ОЕОю ОЉОаОЎОЎОфОћ.
ОбОЎОДОеОЋОЪ ОќОћ, ОЉОЋ ОћОЊОеОЎОЕОЋОф ОДОЋОЉОбОЋОф ОљОф ОљОЋОцОЪ ОфОЏОаОЋОЪ ОЋОЉОаОЎОЎОф ОћОъОбОеОЏОф ОфОДОБ ОњОЮ ОюОЉОДОеОЎ PID. ОюОљОЌОе ОаОЎОАОЋОЌ ОЕОю ОћОЊОеОЎОЕОЋОф ОЋОћОћОфОаОћОњОЋОф ОћОеОдОЋОЎОћ ОЕОю ОъОбОеОЏОф ОћОЉОДОеОћ, ОаОЎОфОЪ ОюОфОЏОаОЪ ОљОф ОћОЉОДОе ОЋОюОЉОЌОЋОЪ ОљОф ОљОЋОцОЪ ОћОЕОцОбОфОЋ ОбОю ОћОъОбОеОЏОф. ОцОбОъОЎОЮ ОеОЉОЋОф, ОЏОцОЎ ОЕОДОЋОеОћ ОЉОъОбОеОЏОЋОф ОћОаОЊОАОЎОЋОф ОеОЉОЋОф, ОћОфОћОюОЎОџ ОЎОфОЉОеОе ОЏОфОћОюОЎОџ ОљОЎОўОеОўОЎОЉОЎ, ОЉОЋ ОъОфОЋОЏОаОЪ ОЉОДОе, ОаОЉОЌОаОЋОф ОћОфОЋОдОљОЋОф, ОЋОюОљОЌОе ОъОЏОЪ ОаОбОЕОЎОЮ ОЕОЎОаОЋОЎОЎОЮ ОЉОъОЎОЊОћ ОЋОЎОЕ ОдОЋОеОџ ОЉОЏОџ. ОЎОЕОаОЪ ОЕОЎОўОЋОф ОЋОњОЎОЕОЋОф ОеОЉОЋОф ОюОЏОЋОЋОаОЋОЪ ОЉОДОеОЎ PID, ОЋОћОћОЌОюОўОћ ОЉОљОЎОќОЋ ОъОћОЪ ОюОћОЕОфОъОЕ ОбОЕОЋОЎОћ ОюОћОЕОфОаОЋОф ОЉОћОфОљОЮ ОюОъОбОеОЏОф ОЋОюОЊОеОЎОЕОЋОф ОъОъОаОћ, ОюОъОЎОЊОб ОћОаОфОЋОЪ ОЉОЎОЊОЎОЊ ОћОъОфОЏОаОЪ, ОЉОћОбОЊОцОЋОф ОћОъОфОЏОаОЪ ОЋОбОЋОЊ. ОЏОЕОљОаОЋ ОбОЋОАОДОЎОЮ ОЉОфОЏОаОЋОЪ ОЉОДОе ОюОъОбОеОЏОф, ОЎОЕ ОЉОЊОеОџ ОЏОюОю ОЕОаОЎ ОъОдОЉОЎОЮ ОљОцОЕОеОЎОЎОЮ:
- ОъОдОЉ ОљОЌОЊ ОћОЋОљ ОъОдОЉ ОЉОЋ ОЎОЕ ОюОаОЋ ОъОЋОЊОю ОъОфОъОўОЎ ОЕОю ОћОъОбОеОЏОф ОЏОъОЋ ОАОў ОъОЕОЋОЋОљОЋОф ОЊОЎОцОеОаОдОЎОљОюОЎОЋОф, ОъОеОЌОЉ ОъОдОЉ, ОцОЋОаОДОдОЎОЋОф ОфОъОАОЋОеОф ОљОЋ ОЊОЎОљОњОеОъОф ОЉОюОЋОДОЎОЮ. ОЎОЏОЋОю ОюОћОЎОЋОф ОЕОљОф ОћОъОЋОЊОю ОЉОаОЎОаОЋ ОЉОбОдОъОаОЋ ОљОЋ ОЕОДОЎОЉОюОаОЋ ОљОЋОфОЋ ОЏОцОЎ ОЕОћОЋОљ ОъОъОДОЋОЮ ОљОЌОе, ОЏОњОЋОЪ ОдОЋОЋОф ОъОАОЋОЎОЮ ОЉОЌОЉОеОћ ОЉОћ ОљОаОЋ ОбОЋОЉОЊОЎОЮ.
- ОъОдОЉ ОљОЌОе ОћОЋОљ ОЏОќОћ ОЉОЋ ОљОЎОЪ ОюОаОЋ ОъОЋОЊОю ОъОфОъОўОЎ ОЕОю ОћОъОбОеОЏОф, ОљОюОљ ОљОф ОћОъОбОеОЏОф ОЉОцОЋОбОю. ОюОЊОЋОњОъОћ, ОљОЮ ОаОДОаОћ ОеОЌОцОЪ ОЋОаОеОдОћ ОюОћОЋОАОЎОБ ОюОЋ ОъОбОеОЏОф ОЉОДОеОћ, ОюОљ ОаОДОЉОю ОЎОЌОЊ ОбОЮ ОћОеОЌОцОЪ ОъОЋОЊОю ОъОфОъОўОЎ ОљОф ОћОъОфОљОе ОљОф ОћОфОаОћОњОЋОф ОћОеОЌОцОЪ ОЏОфОюОЋОф ОЉОЏОаОЎОАОЋОф, ОљОюОљ ОљОф ОћОъОбОеОЏОф ОћОцОЎОќОЎОф ОЉОюОЉОЊ.
ОбОЉОЋОе ОЏОю ОљОЌОЊ ОъОъОдОЉОЎОЮ ОљОюОЋ ОЎОЕОаОЪ ОъОАОцОе ОЊОеОЏОЎОЮ ОЉОћОЪ ОљОцОЕОе ОаОЎОфОЪ ОюОћОъОЕОЎОџ ОюОбОЉОЋОЊ ОЋОюОфОЏОаОЪ ОљОф ОъОбОеОЏОф ОћОЉОДОеОћ. ОЌОЕОЋОЉ ОюОћОЊОњОЎОЕ ОЏОЎ ОцОбОъОЎОЮ ОеОЉОЋОф, ОюОљОЌОе ОЕОЎОъОЋОЕ ОЉОЏОю ОљОЌОф ОъОћОЕОЎОўОЋОф ОЕОЎОфОЋОљОеОЋ ОљОЋ ОЉОЕОЎОюОЋОЉ ОЕОюОћОЪ, ОЎОЎОЊОеОЕ ОћОъОфОЏОаОЪ ОюОћОЋОАОЎОБ ОЏОЋОЋОаОЋОЪ ОаОЋОАОБ ОюОљОЌОе ОЉОЌОЎОаОф ОЉОЎОдОЋОбОЎ ОћОъОбОеОЏОф ОЉОцОЋОбОю ОюОЕОЮ ОДОЉОюОф ОћОЉОЎОдОЋОбОЎОЮ ОћОЊОеОЋОЕОЎОЮ. ОЏОљОЪ ОЉОљОћ ОюОЎОЊОЎ ОЉОЎОўОЋОЎ ОъОЕОъОбОЋОфОЎ ОцОЕОўОЋОфОћ ОЕОю ОЉОДОеОф PID РђЊ ОњОЮ ОюОљОЌОе ОДОЉОЎОбОф ОбОеОЏОЎОЮ ОюОЉОДОе, ОаОЎОфОЪ ОюОћОъОЕОЎОџ ОЋОюОЕОаОЋОф ОљОЋОфОЮ ОфОЋОџ ОЎОЊОЎОбОф ОћОДОЕОеОЎОЮ ОЉОЎОЪ ОћОДОЉОЋОбОЎОЮ ОћОЕОЋОаОЎОЮ ОюОћОфОаОћОњОЋОф ОћОъОбОеОЏОф, ОњОЮ ОбОю ОЎОЊОЎ ОъОЕОфОъОЕ ОћОДОдОћ ОЕОъОЕОфОъОЕ ОЉОъОбОеОЏОф ОЉОцОЋОбОю. ОЊОЉОе ОќОћ ОъОљОцОЕОе ОюОЎОдОЋОе ОЉОДОе PID ОћОбОЋОаОћ ОюОдОеОЏОЎОЮ ОъОАОЋОЎОъОЎОЮ, ОЋОбОЮ ОќОљОф ОъОљОцОЕОе ОюОъОЕОфОъОЕОЎОЮ ОљОЌОеОЎОЮ ОюОЕОаОЋОф ОљОЋОфОЋ ОЉОћОфОљОЮ ОюОћОбОЊОцОЋОф ОљОЌОеОЋОф ОЉОДОюОЋОф ОеОЉОћ ОЋОъОЉОюОЎ ОюОћОЌОќОЎОД ОЉОЎОЊОб ОъОбОъОЎОД ОЉОъОЎОЋОЌОЊ ОЉОфОЎОљОЋОеОЎОћ ОћОбОЋОъОЊОф ОъОљОЌОЋОеОЎ ОћОЉОДОе.
ОЏОЋОЋОаОЋОЪ ОЉОДОе ОЉОћОЎОаОфОЪ ОъОЋОЊОю ОъОфОъОўОЎ ОЕОю ОћОъОбОеОЏОф
ОДОЎОЋОъОЋ ОЕОю ОъОЋОЊОю ОъОфОъОўОЎ ОЕОю ОћОъОбОеОЏОф ОљОЋОфОћ ОъОбОЋОаОЎОЎОаОЎОЮ ОюОЉОДОе ОцОЋОфОЌ ОљОцОЕОеОЋОЎОЋОф ОћОъОЕОфОъОЕОЋОф ОЉОЏОюОЎОЮ ОъОфОъОўОЎОЎОЮ ОбОю ОъОаОф ОюОфОЏОаОЪ ОљОф ОЌОЋОњ ОћОЉОДОеОћ ОЕОю ОћОъОбОеОЏОф. ОЏОюОЎОЮ ОљОюОЋ ОаОЏОюОюОЎОЮ ОЉОфОЌОЋОЮ ОфОЋОеОф ОћОЉОДОеОћ, ОЋОъОўОеОфОЮ ОюОъОдОЋОљ ОљОф ОбОеОЏОЎ ОћОЉОДОе ОћОљОЋОцОўОЎОъОюОЎОЮ ОћОъОъОюОљОЎОЮ ОљОф ОћОЊОеОЎОЕОЋОф. ОЉОљОЋОцОЪ ОЏОюОюОЎ, ОаОЎОфОЪ ОюОЌОюОД ОљОф ОЕОЎОўОЋОф ОћОЏОЋОЋОаОЋОЪ ОћОъОЉОЋОАОАОЋОф ОбОю ОъОЋОЊОю ОъОфОъОўОЎ ОюОЕОфОЎ ОДОЉОЋОдОЋОф ОЕОЋОаОЋОф:
- ОЏОЋОЋОаОЋОЪ ОЎОЊОаОЎ/ОљОаОюОЎОўОЎ: ОъОЕОъОбОЋОф ОћОЊОЉОе ОћОЎОљ ОЕОљОаОЋ ОъОаОфОЌОЎОЮ ОљОф ОћОъОЋОЊОю ОћОъОфОъОўОЎ ОЉОбОќОеОф ОбОДОеОЋОаОЋОф ОфОЋОеОф ОћОЉОДОеОћ, ОЋОъОфОЏОаОаОЎОЮ ОљОф ОћОЉОДОе ОЉОћОфОљОЮ. ОЎОЕОаОЪ ОЕОЎОўОЋОф ОеОЉОЋОф ОюОбОЕОЋОф ОќОљОф, ОљОЋОюОЮ ОаОЎОфОЪ ОюОћОќОЏОЎОе ОъОАОцОе ОЕОЎОўОЋОф ОаОцОЋОдОЋОф:
 ОљОЋОцОЪ ОћОдОњОф ОДОўОЉОЎ ОъОбОеОЏОф ОЉОъОЎОЕОЋОе ОюОцОюОА (ОъОЎОЕОЋОе ОъОеОЋОЏОЉ ОћОъОЕОъОЕ ОюОЎОЎОдОЋОњ ОћОфОъОеОЋОф ОюОцОюОА). ОДОўОЉОЎ ОћОъОбОеОЏОф ОъОАОЋОъОаОЎОЮ ОЉ-X ОЋОћОљОцОАОЎОЮ ОЕОюОћ ОЉ-O.ОъОЎОДОЋОЮ ОДОўОЉОЎОЮ: ОљОЌОф ОћОЊОеОЏОЎОЮ ОћОаОцОЋОдОЋОф ОюОфОЎОљОЋОе ОъОбОеОЏОф ОЉОДОеОћ ОћОЎОљ ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф. ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОћОЎОљ ОъОЕОЋОЋОљОћ ОъОфОъОўОЎОф ОћОъОфОДОЉОюОф ОбОю ОЎОЊОЎ ОЉОЎОдОЋОб ОћОфОъОеОф ОюОцОюОА ОбОю ОћОъОЕОЋОЋОљОЋОф ОћОЊОЎОцОеОаОдОЎОљОюОЎОЋОф ОћОъОфОљОеОЋОф ОљОф ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЉОќОъОЪ, ОЋОћОЎОљ ОъОфОљОеОф ОљОф ОћОДОЕОе ОЉОЎОЪ ОћОЏОаОЎОАОћ ОюОъОбОеОЏОф ОюОЎОдОЎОљОфОћ (ОЏОљОЕОе ОЕОфОЎ ОћОљОЌОеОЋОаОЋОф ОаОфОЋОаОЋОф ОЉОъОЎОЕОЋОе ОюОцОюОА ОњОЮ ОЏОЪ). ОљОЌОЊ ОћОЎОфОеОЋОаОЋОф ОћОъОЕОъОбОЋОфОЎОЎОЮ ОЉОЕОЎОъОЋОЕ ОЉОцОЋОаОДОдОЎОЋОф ОфОъОАОЋОеОф ОюОфОЎОљОЋОе ОъОбОеОЏОф ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОаОњОќОеОф ОЉОъОЎОЕОЋОе ОћОќОъОЪ ОћОЋОцОЏОЋОф ОюОъОЏОцОюОЋОф ОЉОъОЎОЕОЋОе ОюОцОюОА, ОЊОЉОе ОћОћОЋОцОџ ОъОЕОЋОЋОљОЋОф ОЊОЎОцОеОаОдОЎОљОюОЎОЋОф ОюОцОЋОюОЎОаОЋОъОЎОЮ, ОћОДОюОЎОЮ ОЉОћОеОЉОћ ОюОаОЎОфОЋОЌ ОъОфОъОўОЎ. ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОЏОюОюОЎОф ОаОЎОфОаОф ОюОфОЎОљОЋОе ОЉОљОЋОцОЪ ОћОЉОљ:
ОљОЋОцОЪ ОћОдОњОф ОДОўОЉОЎ ОъОбОеОЏОф ОЉОъОЎОЕОЋОе ОюОцОюОА (ОъОЎОЕОЋОе ОъОеОЋОЏОЉ ОћОъОЕОъОЕ ОюОЎОЎОдОЋОњ ОћОфОъОеОЋОф ОюОцОюОА). ОДОўОЉОЎ ОћОъОбОеОЏОф ОъОАОЋОъОаОЎОЮ ОЉ-X ОЋОћОљОцОАОЎОЮ ОЕОюОћ ОЉ-O.ОъОЎОДОЋОЮ ОДОўОЉОЎОЮ: ОљОЌОф ОћОЊОеОЏОЎОЮ ОћОаОцОЋОдОЋОф ОюОфОЎОљОЋОе ОъОбОеОЏОф ОЉОДОеОћ ОћОЎОљ ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф. ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОћОЎОљ ОъОЕОЋОЋОљОћ ОъОфОъОўОЎОф ОћОъОфОДОЉОюОф ОбОю ОЎОЊОЎ ОЉОЎОдОЋОб ОћОфОъОеОф ОюОцОюОА ОбОю ОћОъОЕОЋОЋОљОЋОф ОћОЊОЎОцОеОаОдОЎОљОюОЎОЋОф ОћОъОфОљОеОЋОф ОљОф ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЉОќОъОЪ, ОЋОћОЎОљ ОъОфОљОеОф ОљОф ОћОДОЕОе ОЉОЎОЪ ОћОЏОаОЎОАОћ ОюОъОбОеОЏОф ОюОЎОдОЎОљОфОћ (ОЏОљОЕОе ОЕОфОЎ ОћОљОЌОеОЋОаОЋОф ОаОфОЋОаОЋОф ОЉОъОЎОЕОЋОе ОюОцОюОА ОњОЮ ОЏОЪ). ОљОЌОЊ ОћОЎОфОеОЋОаОЋОф ОћОъОЕОъОбОЋОфОЎОЎОЮ ОЉОЕОЎОъОЋОЕ ОЉОцОЋОаОДОдОЎОЋОф ОфОъОАОЋОеОф ОюОфОЎОљОЋОе ОъОбОеОЏОф ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОаОњОќОеОф ОЉОъОЎОЕОЋОе ОћОќОъОЪ ОћОЋОцОЏОЋОф ОюОъОЏОцОюОЋОф ОЉОъОЎОЕОЋОе ОюОцОюОА, ОЊОЉОе ОћОћОЋОцОџ ОъОЕОЋОЋОљОЋОф ОЊОЎОцОеОаОдОЎОљОюОЎОЋОф ОюОцОЋОюОЎОаОЋОъОЎОЮ, ОћОДОюОЎОЮ ОЉОћОеОЉОћ ОюОаОЎОфОЋОЌ ОъОфОъОўОЎ. ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОЏОюОюОЎОф ОаОЎОфОаОф ОюОфОЎОљОЋОе ОЉОљОЋОцОЪ ОћОЉОљ:  . ОЕОЋОеОЕОЎ ОцОЋОюОЎОаОЋОЮ ОћОъОЋОаОћ ОаОДОеОљОЎОЮ ОЕОЋОеОЕОЎОЮ (ОЕОЏОЪ ОћОЮ ОњОЋОеОъОЎОЮ ОюОљОЎОцОЋОА ОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф), ОЋОЕОЋОеОЕОЎ ОцОЋОюОЎОаОЋОЮ ОћОъОЏОаОћ ОаОДОеОљОЎОЮ ОДОўОЉОЎОЮ (ОъОЕОЋОЮ ОЕОљОЎОцОЋОА ОћОъОЋОаОћ ОњОЋОеОЮ ОюОбОеОџ ОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф ОюОЕОљОЋОБ ОюОљОЎОаОАОЋОБ). ОбОеОЏОЎОћОЮ ОЕОю ОћОљОцОАОЎОЮ ОЋОћОЕОЋОеОЕОЎОЮ ОаОфОЋОаОЎОЮ ОбОю ОЎОЊОЎ ОъОАОцОеОЎОЮ ОъОеОЋОЏОЉОЎОЮ, ОЋОћОЮ ОљОюОЋ ОћОДОЋОЉОбОЎОЮ ОЏОЎОдОЊ ОфОфОаОћОњ ОћОъОбОеОЏОф РђЊ ОћОљОЮ ОћОЎОљ ОфОњОЎОЉ ОъОћОе ОюОЕОЎОаОЋОЎОЎОЮ ОЉОЏОаОЎОАОЋОф, ОћОљОЮ ОћОЎОљ ОфОфОаОЋОЊ, ОћОљОЮ ОћОЎОљ ОфОћОЎОћ ОЎОдОЎОЉОћ ОЋОбОЋОЊ. ОЎОЕ ОюОдОЎОЎОЪ ОЕОДОЕОеОЎОЮ ОЉОЎОЪ ОЏОаОЎОАОЋОф ОЕОЋОаОЋОф ОюОЎОдОЎОљОЋОф ОЕОЋОаОЋОф ОЉОљОЋОфОћ ОћОъОбОеОЏОф ОаОфОЋОаОЎОЮ ОбОю ОЎОЊОЎ ОцОЋОаОДОдОЎОЋОф ОфОъОАОЋОеОф ОЕОЋОаОЋОф, ОЏОюОЋОъОе РђЊ ОћОДОЕОе ОЉОЎОЪ ОћОцОеОбОћ ОюОЎОдОЎОљОф ОћОъОбОеОЏОф ОюОљ ОЎОћОЎОћ ОќОћОћ ОюОДОЕОе ОЕОЉОЎОЪ ОљОЋОф ОћОЎОЎОЌОЋОА ОюОЎОдОЎОљОфОћ, ОЋОћОЋОљ ОЎОфОЋОљОе ОбОю ОЎОЊОЎ ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОЕОЋОаОћ. ОъОЏОЎОЋОЋОЪ ОЕОћОЉОДОе ОћОЋОљ ОЉОбОю ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОъОЕОюОЋ, ОћОЏОаОАОфОЋ ОюОЌОЋОњ ОћОАОњОЋОе ОъОЕОцОЎОбОћ ОбОю ОцОЋОаОДОдОЎОЋОф ОћОфОъОАОЋОеОф ОћОЕОЋОаОЋОф ОЕОю ОћОъОбОеОЏОф. ОъОЏОЎОЋОЋОЪ ОЕОЏОџ, ОаОЎОфОЪ ОюОћОЕОцОЎОб ОбОю ОъОЎОДОЋОЮ ОћОДОўОЉОЎОЮ ОЋОћОљОцОАОЎОЮ ОЕОю ОћОъОбОеОЏОф ОбОю ОЎОЊОЎ ОЕОЎОаОЋОЎ ОбОеОЏОЎ ОћОЉОДОе, ОЋОЉОЏОџ ОюОћОЕОЎОњ ОЉОЎОдОЋОбОЎОЮ ОеОдОЋОЎОЎОЮ. ОћОЌОЎОАОеОЋОЪ ОЉОЕОЎОўОћ ОќОЋ ОћОЋОљ ОЕОћОЎОљ ОЊОЋОеОЕОф ОћОЉОаОћ ОўОЋОЉОћ ОЕОю ОћОбОДОеОЋОаОЋОф ОћОъОфОъОўОЎОЎОЮ ОћОДОЋОЕОеОЎОЮ ОЉОЎОЪ ОъОЎОДОЋОЮ ОћОДОўОЉОЎОЮ ОЋОћОљОцОАОЎОЮ ОЉОъОЎОЕОЋОе ОћОъОеОЋОЏОЉ ОюОЉОЎОЪ ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф, ОЋОюОЏОЪ ОћОЎОљ ОцОЌОЋОф ОљОЎОаОўОЋОљОЎОўОЎОЉОЎОф ОЋОДОюОћ ОюОЎОЎОЕОЋОЮ ОбОЉОЋОе ОъОЕОфОъОЕОЎОЮ ОЕОљОЎОаОЮ ОЉОДОЎОљОЎОЮ ОЉОДОЕОеОЎОЮ ОљОюОЋ.
. ОЕОЋОеОЕОЎ ОцОЋОюОЎОаОЋОЮ ОћОъОЋОаОћ ОаОДОеОљОЎОЮ ОЕОЋОеОЕОЎОЮ (ОЕОЏОЪ ОћОЮ ОњОЋОеОъОЎОЮ ОюОљОЎОцОЋОА ОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф), ОЋОЕОЋОеОЕОЎ ОцОЋОюОЎОаОЋОЮ ОћОъОЏОаОћ ОаОДОеОљОЎОЮ ОДОўОЉОЎОЮ (ОъОЕОЋОЮ ОЕОљОЎОцОЋОА ОћОъОЋОаОћ ОњОЋОеОЮ ОюОбОеОџ ОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф ОюОЕОљОЋОБ ОюОљОЎОаОАОЋОБ). ОбОеОЏОЎОћОЮ ОЕОю ОћОљОцОАОЎОЮ ОЋОћОЕОЋОеОЕОЎОЮ ОаОфОЋОаОЎОЮ ОбОю ОЎОЊОЎ ОъОАОцОеОЎОЮ ОъОеОЋОЏОЉОЎОЮ, ОЋОћОЮ ОљОюОЋ ОћОДОЋОЉОбОЎОЮ ОЏОЎОдОЊ ОфОфОаОћОњ ОћОъОбОеОЏОф РђЊ ОћОљОЮ ОћОЎОљ ОфОњОЎОЉ ОъОћОе ОюОЕОЎОаОЋОЎОЎОЮ ОЉОЏОаОЎОАОЋОф, ОћОљОЮ ОћОЎОљ ОфОфОаОЋОЊ, ОћОљОЮ ОћОЎОљ ОфОћОЎОћ ОЎОдОЎОЉОћ ОЋОбОЋОЊ. ОЎОЕ ОюОдОЎОЎОЪ ОЕОДОЕОеОЎОЮ ОЉОЎОЪ ОЏОаОЎОАОЋОф ОЕОЋОаОЋОф ОюОЎОдОЎОљОЋОф ОЕОЋОаОЋОф ОЉОљОЋОфОћ ОћОъОбОеОЏОф ОаОфОЋОаОЎОЮ ОбОю ОЎОЊОЎ ОцОЋОаОДОдОЎОЋОф ОфОъОАОЋОеОф ОЕОЋОаОЋОф, ОЏОюОЋОъОе РђЊ ОћОДОЕОе ОЉОЎОЪ ОћОцОеОбОћ ОюОЎОдОЎОљОф ОћОъОбОеОЏОф ОюОљ ОЎОћОЎОћ ОќОћОћ ОюОДОЕОе ОЕОЉОЎОЪ ОљОЋОф ОћОЎОЎОЌОЋОА ОюОЎОдОЎОљОфОћ, ОЋОћОЋОљ ОЎОфОЋОљОе ОбОю ОЎОЊОЎ ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОЕОЋОаОћ. ОъОЏОЎОЋОЋОЪ ОЕОћОЉОДОе ОћОЋОљ ОЉОбОю ОцОЋОаОДОдОЎОЎОф ОфОъОАОЋОеОф ОъОЕОюОЋ, ОћОЏОаОАОфОЋ ОюОЌОЋОњ ОћОАОњОЋОе ОъОЕОцОЎОбОћ ОбОю ОцОЋОаОДОдОЎОЋОф ОћОфОъОАОЋОеОф ОћОЕОЋОаОЋОф ОЕОю ОћОъОбОеОЏОф. ОъОЏОЎОЋОЋОЪ ОЕОЏОџ, ОаОЎОфОЪ ОюОћОЕОцОЎОб ОбОю ОъОЎОДОЋОЮ ОћОДОўОЉОЎОЮ ОЋОћОљОцОАОЎОЮ ОЕОю ОћОъОбОеОЏОф ОбОю ОЎОЊОЎ ОЕОЎОаОЋОЎ ОбОеОЏОЎ ОћОЉОДОе, ОЋОЉОЏОџ ОюОћОЕОЎОњ ОЉОЎОдОЋОбОЎОЮ ОеОдОЋОЎОЎОЮ. ОћОЌОЎОАОеОЋОЪ ОЉОЕОЎОўОћ ОќОЋ ОћОЋОљ ОЕОћОЎОљ ОЊОЋОеОЕОф ОћОЉОаОћ ОўОЋОЉОћ ОЕОю ОћОбОДОеОЋОаОЋОф ОћОъОфОъОўОЎОЎОЮ ОћОДОЋОЕОеОЎОЮ ОЉОЎОЪ ОъОЎОДОЋОЮ ОћОДОўОЉОЎОЮ ОЋОћОљОцОАОЎОЮ ОЉОъОЎОЕОЋОе ОћОъОеОЋОЏОЉ ОюОЉОЎОЪ ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф, ОЋОюОЏОЪ ОћОЎОљ ОцОЌОЋОф ОљОЎОаОўОЋОљОЎОўОЎОЉОЎОф ОЋОДОюОћ ОюОЎОЎОЕОЋОЮ ОбОЉОЋОе ОъОЕОфОъОЕОЎОЮ ОЕОљОЎОаОЮ ОЉОДОЎОљОЎОЮ ОЉОДОЕОеОЎОЮ ОљОюОЋ. ОъОдОЎОљОф ОбОЋОЊОцОЎ ОЎОдОЎОЉОЋОф ОЉОбОќОеОф ОЊОЎОљОњОеОъОф ОЉОЋОЊОћ. ОЊОеОЎОЮ ОаОцОЋОдОЋОф ОаОЋОАОцОф ОюОЉОЊОЎОДОф ОбОЋОЊОцОЎ ОЎОдОЎОЉОЋОф ОћОЌОЋОњ ОћОАОњОЋОе ОћОЎОљ ОбОДОЋОъОф ОаОЎОЎОДОЋОЋОЎОАОў ОЋОбОДОЋОъОф ОаОЎОДОЋОюОА.ОбОЎОдОЋОЉ ОЌОЋОњ: ОљОЌОф ОћОЕОЎОўОЋОф ОћОаОцОЋОдОЋОф ОюОфОЏОаОЋОЪ ОъОбОеОЏОф ОЉОДОеОћ ОћОЎОљ ОЕОЎОъОЋОЕ ОЉОфОЏОЋОаОЋОф ОћОЌОЋОњ ОћОцОфОЋОЌ (ОЕОљОЎОаОЋ ОЏОЋОюОю ОъОЕОЋОЉ) ОбОю ОъОаОф ОюОћОЉОЎОЪ ОЋОюОдОцОЋОф ОЏОЎОдОЊ ОЎОфОаОћОњ ОћОЌОЋОњ ОћОАОњОЋОе. ОЕОЎОўОЋОф ОљОюОЋ ОцОЋОфОЌОЋ ОЉОЕОю ОћОбОЋОЉОЊОћ ОЕОцОбОъОЎОЮ ОеОЉОЋОф ОДОю ОЎОЋОфОе ОюОаОфОЌ ОъОфОъОўОЎОф ОљОф ОћОфОаОћОњОЋОф ОћОЌОЋОњ ОћОцОфОЋОЌ ОЋОъОЕОЮ ОюОћОЉОЎОЪ ОЏОЎОдОЊ ОфОфОаОћОњ ОћОъОбОеОЏОф ОЉОћОЎОаОфОЪ ОЌОЋОњ ОАОњОЋОе, ОЏОљОЕОе ОћОЊОЉОе ОћОЎОћ ОъОЕОъОбОЋОфОЎ ОбОЋОЊ ОЎОЋОфОе ОЏОљОЕОе ОЎОЏОЋОюОЋОф ОћОъОЌОЕОЋОЉ ОюОљ ОћОЎОЋ ОъОфОДОЊОъОЋОф ОЏОцОЎ ОЕОћОЪ ОћОЎОЋОЮ, ОЋОћОњОЎОЕОћ ОюОъОЌОЕОЉОЎОЮ ОћОЎОЎОфОћ ОъОЋОњОЉОюОф ОЉОћОеОЉОћ[12]. ОЏОюОЎОЮ ОљОюОЋ ОъОљОцОЕОеОЎОЮ ОЉОЊОЎОДОћ ОъОћОЎОеОћ ОЕОю ОбОЋОЊОцОЎ ОћОЎОдОЎОЉОЋОф ОЕОю ОћОъОбОеОЏОф (ОћОДОЋОЉОбОЎОЮ, ОЉОљОЋОцОЪ ОбОДОеОЋОаОЎ, ОбОЊ ОЏОъОћ ОћОъОбОеОЏОф ОЎОдОЎОЉОћ) ОЋОбОЋОЊ. ОћОЏОюОЎОЮ ОЉОћОЮ ОаОЎОфОЪ ОюОћОЕОфОъОЕ ОюОбОЎОдОЋОЉ ОћОЌОЋОњ ОеОЉОЎОЮ, ОЏОљОЕОе ОћОЉОЋОюОўОЎОЮ ОЕОЉОћОЮ ОћОЮОЮ ОбОДОЋОъОф ОЉОЋОЊОћ, ОбОДОЋОъОф ОаОЎОЎОДОЋОЋОЎОАОў ОЋОбОДОЋОъОф ОаОЎОДОЋОюОА. ОЉОаОЋОАОБ ОюОљОюОЋ ОаОЎОфОЪ ОюОћОќОЏОЎОе ОњОЮ ОљОф ОДОеОЎОўОеОЎОЋОЪ ОеОљОЋОў-ОћОЋОеОЋОЉОЎОЦ ОюОЎОдОЎОЉОЋОф ОъОбОеОЏОЋОф ОЋОљОф ОћОЕОЎОъОЋОЕ ОЉОъОњ"ОЕ (ОъОЎОДОЋОЮ ОњОљОЋОъОўОеОЎ ОЕОЋОеОЕОЎОЮ[13]) ОћОъОфОљОе ОљОф ОћОЕОфОаОЋОф ОъОЎОДОЋОЮ ОДОўОЉОЎ ОћОЌОЋОњ ОћОАОњОЋОе ОЏОфОюОЋОф ОЉОћОњОЉОе ОћОЉОДОе.
ОъОдОЎОљОф ОбОЋОЊОцОЎ ОЎОдОЎОЉОЋОф ОЉОбОќОеОф ОЊОЎОљОњОеОъОф ОЉОЋОЊОћ. ОЊОеОЎОЮ ОаОцОЋОдОЋОф ОаОЋОАОцОф ОюОЉОЊОЎОДОф ОбОЋОЊОцОЎ ОЎОдОЎОЉОЋОф ОћОЌОЋОњ ОћОАОњОЋОе ОћОЎОљ ОбОДОЋОъОф ОаОЎОЎОДОЋОЋОЎОАОў ОЋОбОДОЋОъОф ОаОЎОДОЋОюОА.ОбОЎОдОЋОЉ ОЌОЋОњ: ОљОЌОф ОћОЕОЎОўОЋОф ОћОаОцОЋОдОЋОф ОюОфОЏОаОЋОЪ ОъОбОеОЏОф ОЉОДОеОћ ОћОЎОљ ОЕОЎОъОЋОЕ ОЉОфОЏОЋОаОЋОф ОћОЌОЋОњ ОћОцОфОЋОЌ (ОЕОљОЎОаОЋ ОЏОЋОюОю ОъОЕОЋОЉ) ОбОю ОъОаОф ОюОћОЉОЎОЪ ОЋОюОдОцОЋОф ОЏОЎОдОЊ ОЎОфОаОћОњ ОћОЌОЋОњ ОћОАОњОЋОе. ОЕОЎОўОЋОф ОљОюОЋ ОцОЋОфОЌОЋ ОЉОЕОю ОћОбОЋОЉОЊОћ ОЕОцОбОъОЎОЮ ОеОЉОЋОф ОДОю ОЎОЋОфОе ОюОаОфОЌ ОъОфОъОўОЎОф ОљОф ОћОфОаОћОњОЋОф ОћОЌОЋОњ ОћОцОфОЋОЌ ОЋОъОЕОЮ ОюОћОЉОЎОЪ ОЏОЎОдОЊ ОфОфОаОћОњ ОћОъОбОеОЏОф ОЉОћОЎОаОфОЪ ОЌОЋОњ ОАОњОЋОе, ОЏОљОЕОе ОћОЊОЉОе ОћОЎОћ ОъОЕОъОбОЋОфОЎ ОбОЋОЊ ОЎОЋОфОе ОЏОљОЕОе ОЎОЏОЋОюОЋОф ОћОъОЌОЕОЋОЉ ОюОљ ОћОЎОЋ ОъОфОДОЊОъОЋОф ОЏОцОЎ ОЕОћОЪ ОћОЎОЋОЮ, ОЋОћОњОЎОЕОћ ОюОъОЌОЕОЉОЎОЮ ОћОЎОЎОфОћ ОъОЋОњОЉОюОф ОЉОћОеОЉОћ[12]. ОЏОюОЎОЮ ОљОюОЋ ОъОљОцОЕОеОЎОЮ ОЉОЊОЎОДОћ ОъОћОЎОеОћ ОЕОю ОбОЋОЊОцОЎ ОћОЎОдОЎОЉОЋОф ОЕОю ОћОъОбОеОЏОф (ОћОДОЋОЉОбОЎОЮ, ОЉОљОЋОцОЪ ОбОДОеОЋОаОЎ, ОбОЊ ОЏОъОћ ОћОъОбОеОЏОф ОЎОдОЎОЉОћ) ОЋОбОЋОЊ. ОћОЏОюОЎОЮ ОЉОћОЮ ОаОЎОфОЪ ОюОћОЕОфОъОЕ ОюОбОЎОдОЋОЉ ОћОЌОЋОњ ОеОЉОЎОЮ, ОЏОљОЕОе ОћОЉОЋОюОўОЎОЮ ОЕОЉОћОЮ ОћОЮОЮ ОбОДОЋОъОф ОЉОЋОЊОћ, ОбОДОЋОъОф ОаОЎОЎОДОЋОЋОЎОАОў ОЋОбОДОЋОъОф ОаОЎОДОЋОюОА. ОЉОаОЋОАОБ ОюОљОюОЋ ОаОЎОфОЪ ОюОћОќОЏОЎОе ОњОЮ ОљОф ОДОеОЎОўОеОЎОЋОЪ ОеОљОЋОў-ОћОЋОеОЋОЉОЎОЦ ОюОЎОдОЎОЉОЋОф ОъОбОеОЏОЋОф ОЋОљОф ОћОЕОЎОъОЋОЕ ОЉОъОњ"ОЕ (ОъОЎОДОЋОЮ ОњОљОЋОъОўОеОЎ ОЕОЋОеОЕОЎОЮ[13]) ОћОъОфОљОе ОљОф ОћОЕОфОаОЋОф ОъОЎОДОЋОЮ ОДОўОЉОЎ ОћОЌОЋОњ ОћОАОњОЋОе ОЏОфОюОЋОф ОЉОћОњОЉОе ОћОЉОДОе.- ОЕОЎОўОЋОф ОћОЎОЋОеОЎОАОўОЎОЋОф: ОЕОЎОўОЋОф ОљОюОЋ ОъОдОЎОбОЋОф "ОъОфОЏОЋОЪ" ОюОЏОЋОЋОаОЋОЪ ОЕОю ОЉОДОе PID (ОљОЋ ОЉОДОе PID ОЌОюОДОЎ) ОбОю ОЉОАОЎОА ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф. ОъОЕОъОбОЋОф ОћОЊОЉОе ОћОЎОљ ОЕОъОфОЉОдОб ОаОЎОАОЋОЎ ОбОю ОћОъОЋОЊОю ОюОДОЉОЎОбОф ОбОеОЏОЎОЮ ОъОАОЋОЎОъОЎОЮ ОћОъОљОцОЎОЎОаОЎОЮ ОљОф ОћОъОбОеОЏОф, ОЋОюОљОЌОе ОъОЏОЪ, ОЉОћОЎОаОфОЪ ОћОбОеОЏОЎОЮ ОЕОћОфОДОЉОюОЋ, ОаОЎОфОЪ ОюОДОЉОЋОб ОљОф ОДОЉОЋОбОЎ ОћОбОаОцОЎОЮ ОћОЕОЋОаОЎОЮ ОЕОю ОћОЉОДОе ОбОю ОцОЎОћОЮ. ОћОЎОфОеОЋОЪ ОЉОЕОЎОўОЋОф ОљОюОЋ ОћОЋОљ ОДОюОЋОф ОћОЏОЋОЋОаОЋОЪ, ОљОЋОюОЮ ОъОЏОЎОЋОЋОЪ ОЕОћОЪ ОюОљ ОфОЋОЏОаОаОЋ ОбОЉОЋОе ОъОбОеОЏОф ОъОАОЋОЎОъОф, ОбОю ОъОфОЏОаОЪ ОъОбОеОЏОф ОћОЉОДОеОћ ОюОЋОЋОЊОљ ОЕОћОфОЋОдОљОЋОф ОћОъОфОДОЉОюОЋОф ОбОю ОЎОЊОЎОћОЪ ОбОЋОаОЋОф ОбОю ОЊОеОЎОЕОЋОфОЎОЋ ОћОАОцОдОЎОцОЎОЋОф. ОЕОфОЎОЎОЮ ОъОћОЕОЎОўОЋОф ОћОЎОЊОЋОбОЋОф ОЉОЎОЋОфОе ОЉОфОЌОЋОЮ ОќОћ ОћОЪ ОЕОЎОўОф ОќОЎОњОюОе-ОаОЎОДОЋОюОА (Ziegler-Nichols method) ОЋОЕОЎОўОф ОЏОћОЪ ОДОЋОЪ (Cohen-Coon method).
- ОЏОЋОЋОаОЋОЪ ОљОЋОўОЋОъОўОЎ: ОЏОЋОЋОаОЋОЪ ОќОћ ОаОбОЕОћ ОбОю ОЎОЊОЎ ОЕОЎОъОЋОЕ ОЉОфОЋОЏОаОћ ОЎОЎОбОЋОЊОЎОф, ОћОъОДОЉОюОф ОљОф ОћОъОЋОЊОю ОћОъОфОъОўОЎ ОЕОю ОћОъОбОеОЏОф ОЋОъОфОљОеОф ОљОф ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЏОфОюОЋОф ОЉОбОеОЏОЎ ОћОЉОДОе ОћОЕОЋОаОЎОЮ. ОЉОъОДОеОЎОЮ ОеОЉОЎОЮ, ОћОљОњОюОЋОеОЎОфОЮ ОћОбОЋОъОЊ ОЉОЉОАОЎОА ОћОфОЋОЏОаОћ ОъОЉОЋОАОА ОбОю ОЕОЎОўОЋОф ОћОЏОЋОЋОаОЋОЪ ОћОЎОЊОаОЎ, ОљОЋОюОЮ ОЕОЎОъОЋОЕ ОЉОфОЋОЏОаОћ ОъОљОцОЕОе ОюОфОЏОаОЪ ОљОф ОЌОЋОњ ОћОЉОДОеОћ ОЉОљОЋОцОЪ ОљОЎОаОўОЋОљОЎОўОЎОЉОЎ ОЋОаОЋОЌ ОЉОћОеОЉОћ ОюОЕОЎОъОЋОЕ. ОюОЊОЋОњОъОћ РђЊ ОЉОЕОЎОъОЋОЕ ОЉОфОЋОЏОаОЋОф ОЏОЋОЋОаОЋОЪ, ОаОЎОфОЪ ОюОљОцОЎОЎОЪ ОљОф ОћОЊОеОЎОЕОЋОф ОъОћОъОбОеОЏОф ОЉОъОЎОЕОЋОе ОћОќОъОЪ (ОЏОњОЋОЪ ОъОљОцОЎОЎОаОЎОЮ ОЕОю ОфОњОЋОЉОф ОћОъОЊОеОњОћ), ОЋОюОДОЉОю ОЉОЌОќОеОћ ОљОф ОбОеОЏОЎ ОћОЉОДОе ОћОЊОеОЋОЕОЎОЮ ОбОю ОъОаОф ОюОћОЕОЎОњ ОЊОеОЎОЕОЋОф ОљОюОЋ.
ОљОЌОЊ ОћОЎОфОеОЋОаОЋОф ОћОњОЊОЋОюОЎОЮ ОЉОбОЉОЋОЊОћ ОбОЮ ОъОЋОЊОю ОъОфОъОўОЎ ОЕОю ОъОбОеОЏОф ОЉОДОеОћ ОћОЋОљ ОћОбОЋОЉОЊОћ ОЕОЉОЎОдОЋОб ОАОЎОъОЋОюОдОЎОЋОф ОъОъОЋОЌОЕОЉОЋОф ОЕОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОЋОф ОДОюОЋОф ОЉОћОеОЉОћ ОюОЉОЎОдОЋОб ОъОљОЕОе ОЉОЎОдОЋОб ОаОЎОАОЋОЎОЎОЮ ОЉОцОЋОбОю РђЊ ОъОЉОЌОЎОаОћ ОъОбОЕОЎОф ОћОЪ ОаОбОЕОЋОф ОюОюОљ ОбОюОЋОф, ОћОЪ ОљОЎОаОЪ ОаОЋОЕОљОЋОф ОАОЎОЏОЋОЪ, ОљОЎОЪ ОдОЋОеОџ ОЉОЌОЋОъОеОћ ОЎОДОеОћ ОЕОцОбОъОЎОЮ ОеОЉОЋОф ОюОљ ОаОЎОфОаОф ОюОЕОЌОќОЋОе ОюОљОЌОе ОаОЎОАОЋОЎ, ОЋОЎОЏОЋОюОЋОф ОюОфОљОе ОфОћОюОЎОЏОЎОЮ ОљОеОЋОЏОЎОЮ ОЉОќОъОЪ ОДОдОе ОъОљОЋОЊ. ОбОЮ ОќОљОф, ОЏОъОЋ ОЉОЏОю ОфОЌОЋОЮ ОћОаОЊОАОЎ, ОЏОъОбОў ОљОБ ОцОбОЮ ОюОљ ОаОЎОфОЪ ОюОЉОАОА ОъОбОеОЏОф ОбОю ОАОЎОъОЋОюОдОЎОЋОф ОЉОюОЉОЊ. ОЊОЉОе ОќОћ ОаОЋОЉОб ОъОњОЋОеОъОЎОЮ ОеОЉОЎОЮ, ОљОЋОюОЮ ОћОбОЎОДОеОЎ ОЕОЉОћОЮ ОћОЋОљ ОћОЎОЏОЋОюОф ОћОъОЋОњОЉОюОф ОюОфОљОе ОљОф ОћОъОдОЎОљОЋОф ОћОљОъОЎОфОЎОф ОЉОЕОюОъОЋОфОћ ОЉОбОќОеОф ОъОЋОЊОюОЎОЮ ОъОфОъОўОЎОЎОЮ, ОъОЋОеОЏОЉОЎОЮ ОЏОЏОю ОЕОЎОћОЎОЋ. ОюОЏОЪ, ОњОЮ ОюОљОЌОе ОЏОЋОЋОаОЋОЪ ОЎОЊОаОЎ ОљОЋ ОљОЋОўОЋОъОўОЎ, ОЏОю ОЌОЋОњ ОЉОДОеОћ ОЎОдОўОеОџ ОюОћОЎОЉОЌОЪ ОбОю ОћОъОбОеОЏОф ОћОљОъОЎОфОЎОф, ОЏОљОЕОе ОцОбОъОЎОЮ ОеОЉОЋОф ОЎОфОЉОеОе ОЕОЎОЕ ОдОЋОеОџ ОЉОЕОЎОаОЋОЎОЎОЮ ОЉОбОеОЏОЎ ОћОЉОДОе ОЕОаОДОЉОбОЋ ОбОю ОАОъОџ ОћОъОЋОЊОю.
ОЏОЋОЋОаОЋОЪ ОЉОДОе ОЉОћОЎОаОфОЪ ОћОъОбОеОЏОф ОЉОцОЋОбОю
ОЏОљОЕОе ОаОфОЋОаОћ ОюОъОЕОфОъОЕ ОћОъОбОеОЏОф ОћОљОъОЎОфОЎОф ОбОюОЎОћ ОЎОЕ ОдОЋОеОџ ОюОЕОюОЋОў, ОаОЎОфОЪ ОюОћОЕОфОъОЕ ОЉОъОАОцОе ОЊОеОЏОЎОЮ ОбОю ОъОаОф ОюОфОЏОаОЪ ОЉОДОе ОъОфОљОЎОЮ:
- ОЏОЋОЋОаОЋОЪ ОЎОЊОаОЎ: ОЏОЋОЋОаОЋОЪ ОъОЕОфОаОЎ ОћОЉОДОе ОфОЋОџ ОЉОЊОЎОДОћ ОЕОю ОљОЋОцОЪ ОћОЕОцОбОфОЮ ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф ОЉОцОЋОбОю. ОћОЎОфОеОЋОЪ ОЉОЕОЎОўОћ ОќОЋ ОћОЋОљ ОћОЉОаОћ ОљОЎОаОўОЋОљОЎОўОЎОЉОЎОф ОЋОЎОЕОЎОеОћ ОЕОю ОљОЋОцОЪ ОћОЕОцОбОф ОЏОю ОљОЌОЊ ОъОћОњОЉОеОЎ ОћОЉОДОе ОбОю ОћОфОаОћОњОЋОф ОћОъОбОеОЏОф, ОЋОЎОЏОЋОюОф ОюОбОЕОЋОф ОќОљОф ОбОю ОЎОЊОЎ ОъОЕОфОъОЕ ОДОдОћ ОЕОљОЎОаОЋ ОъОЉОЎОЪ ОюОбОЋОъОДОЮ ОљОф ОћОДОЕОеОЎОЮ ОћОъОфОъОўОЎОЎОЮ ОЉОЎОЪ ОбОаОцОЎ ОћОЉОДОе ОюОљОЋОцОЪ ОћОЕОцОбОфОЮ ОбОю ОћОъОбОеОЏОф. ОбОЮ ОќОљОф, ОЏОъОЋОЉОЪ ОЕОаОЎОАОЎОЋОЪ ОДОЋОЊОЮ ОЋОћОЉОаОћ ОЕОю ОДОЕОеОЎОЮ ОљОюОЋ ОЎОДОдОеОЋ ОљОф ОћОфОћОюОЎОџ, ОЋОљОБ ОбОЕОЋОЎОЋОф ОюОћОЎОЋОф ОћОЏОеОЌОЎОЋОф ОЉОъОЎОЊОћ ОЋОћОцОбОюОћ ОЕОњОЋОЎОћ ОЕОю ОћОъОбОеОЏОф ОбОюОЋОюОћ ОюОњОеОЋОЮ ОюОаОќОДОЎОЮ.
- ОъОдОЎОљОф ОбОеОЏОЎОЮ ОћОфОЌОюОфОЎОЎОЮ: ОљОцОЕОеОЋОф ОаОЋОАОцОф ОћОЎОљ ОћОцОбОюОћ ОЕОю ОћОъОбОеОЏОф ОбОю ОЎОЊОЎ ОљОЋОфОЋОф ОЏОаОЎОАОћ ОъОАОЋОЎОъОЎОЮ, ОЋОЌОЎОюОЋОЦ ОбОеОЏОЎОЮ ОћОфОЌОюОфОЎОЎОЮ ОюОћОњОЉОеОЎ ОћОЉОДОе ОЉОћОфОљОЮ ОюОфОЋОдОљОЋОф ОћОъОфОДОЉОюОЋОф ОбОю ОцОЎ ОЕОЎОўОЋОф ОЕОЋОаОЋОф. ОЉОъОЎОЊОћ ОЋОъОбОЋОаОЎОЎОаОЎОЮ ОюОЕОцОе ОљОф ОћОфОЋОдОљОЋОф ОаОЎОфОЪ ОюОћОъОЕОЎОџ ОЋОюОЏОЋОЋОаОЪ ОљОф ОћОЉОДОе ОбОЊ ОюОћОњОбОћ ОюОфОЋОдОљОћ ОћОеОдОЋОЎОћ. ОЕОЎОўОЋОф ОаОцОЋОдОЋОф ОюОъОдОЎОљОф ОбОеОЏОЎОЮ ОћОфОЌОюОфОЎОЎОЮ ОћОЪ ОЕОЎОўОф ОќОЎОњОюОе-ОаОЎОДОЋОюОА ОЋОЕОЎОўОф ОЏОћОЪ-ОДОЋОЪ (ОЕОћОЋОќОЏОеОЋ ОњОЮ ОЏОљОцОЕОеОЋОф ОюОЕОЎОъОЋОЕ ОЉОћОЎОаОфОЪ ОъОЋОЊОю ОъОфОъОўОЎ РђЊ ОъОЊОЋОЉОе ОЉОљОЋОфОЪ ОЕОЎОўОЋОф, ОљОЋОюОЮ ОЉОъОДОеОћ ОћОќОћ ОћОбОеОЏОЎОЮ ОћОћОфОЌОюОфОЎОЎОЮ ОъОфОДОЉОюОЎОЮ ОъОаОЎОАОЋОЎ ОљОъОЎОфОЎ ОЕОю ОћОъОбОеОЏОф. ОЉОЕОЎОўОф ОќОЎОњОюОе-ОаОЎОДОЋОюОА ОЎОЕ ОюОћОЎОќОћОе ОЏОљОЕОе ОъОЉОдОбОЎОЮ ОљОЋОфОћ ОбОю ОъОбОеОЏОф ОљОъОЎОфОЎОф, ОъОЏОЎОЋОЋОЪ ОЕОћОЎОљ ОЊОЋОеОЕОф ОћОЉОљОћ ОЕОю ОћОъОбОеОЏОф ОюОАОБ ОћОЎОдОЎОЉОЋОф ОЕОюОћ, ОЊОЉОе ОћОбОюОЋОю ОюОћОќОЎОД ОюОъОбОеОЏОф ОцОЎОќОЎОДОюОЎОф ОљОъОЎОфОЎОф).
 ОЊОЎОљОњОеОъОћ ОћОъОфОљОеОф ОљОф ОћОъОфОЋОЊОЋОф ОћОЕОЋОаОЋОф ОюОќОЎОћОЋОЎ ОъОбОеОЏОЋОф. ОЉОъОДОеОћ ОЕОю "ОДОЋОцОАОћ ОюОЉОаОћ" ОљОаОЋ ОеОЋОљОЎОЮ ОћОЎОўОЉ ОљОф ОъОЉОаОћ ОћОъОбОеОЏОф, ОЋОЉ"ОДОЋОцОАОћ ОЕОЌОЋОеОћ" ОљОЎОаОаОЋ ОЎОЋОЊОбОЎОЮ ОбОюОЎОћ ОЊОЉОе ОъОюОЉОЊ ОљОЋОцОЪ ОћОфОњОЋОЉОћ ОЕОюОћ ОюОЏОаОЎОАОћ. ОъОдОЉ ОЉОЎОаОЎОЎОЮ ОћОЋОљ ОъОдОЉ ОЕОю "ОДОЋОцОАОћ ОљОцОЋОеОћ" ОЉОЋ ОћОЎОЊОб ОЕОюОаОЋ ОбОю ОъОЉОаОћ ОћОъОбОеОЏОф ОЌОюОДОЎ.
ОЊОЎОљОњОеОъОћ ОћОъОфОљОеОф ОљОф ОћОъОфОЋОЊОЋОф ОћОЕОЋОаОЋОф ОюОќОЎОћОЋОЎ ОъОбОеОЏОЋОф. ОЉОъОДОеОћ ОЕОю "ОДОЋОцОАОћ ОюОЉОаОћ" ОљОаОЋ ОеОЋОљОЎОЮ ОћОЎОўОЉ ОљОф ОъОЉОаОћ ОћОъОбОеОЏОф, ОЋОЉ"ОДОЋОцОАОћ ОЕОЌОЋОеОћ" ОљОЎОаОаОЋ ОЎОЋОЊОбОЎОЮ ОбОюОЎОћ ОЊОЉОе ОъОюОЉОЊ ОљОЋОцОЪ ОћОфОњОЋОЉОћ ОЕОюОћ ОюОЏОаОЎОАОћ. ОъОдОЉ ОЉОЎОаОЎОЎОЮ ОћОЋОљ ОъОдОЉ ОЕОю "ОДОЋОцОАОћ ОљОцОЋОеОћ" ОЉОЋ ОћОЎОЊОб ОЕОюОаОЋ ОбОю ОъОЉОаОћ ОћОъОбОеОЏОф ОЌОюОДОЎ.
- ОЉОаОЎОЎОф ОъОЋОЊОю ОъОфОъОўОЎ: ОюОбОЎОфОЎОЮ, ОаОЎОфОЪ ОюОЉОаОЋОф ОъОЋОЊОю ОъОфОъОўОЎ ОбОю ОАОъОџ ОћОъОбОеОЏОф ОћОљОъОЎОфОЎОф. ОюОљОЌОе ОЉОаОЎОЎОф ОћОъОЋОЊОю, ОаОЎОфОЪ ОюОћОЕОфОъОЕ ОЉОЕОЎОўОЋОф ОћОъОфОЋОљОеОЋОф ОъОбОюОћ ОюОЏОЋОЋОаОЋОЪ ОЉОДОе ОЉОћОЎОаОфОЪ ОъОЋОЊОю ОъОфОъОўОЎ. ОЎОЕОаОЪ ОЕОфОЎ ОЊОеОЏОЎОЮ ОаОцОЋОдОЋОф ОюОЉОаОЎОЎОф ОъОЋОЊОю ОъОфОъОўОЎ ОъОфОЋОџ ОъОбОеОЏОф ОцОЎОќОЎОДОюОЎОф:
- ОЎОЊОЎОбОф ОъОЕОЋОЋОљОЋОф ОћОъОбОеОЏОф ОЋОћОњОЊОеОф ОћОаОбОюОъОЎОЮ ОћОЊОеОЋОЕОЎОЮ ОюОЉОбОЎОћ. ОюОљОЌОе ОъОЏОЪ ОаОЎОфОЪ ОюОЉОЌОЋОЪ ОљОф ОћОъОбОеОЏОф ОЋОюОаОАОЋОф ОюОЌОюОЦ ОъОъОаОћ ОљОф ОћОњОЊОюОЎОЮ ОљОЋОфОЮ ОљОаОЋ ОдОеОЎОЏОЎОЮ ОбОю ОъОаОф ОюОфОљОе ОљОф ОћОъОбОеОЏОф ОЉОъОюОЋОљОћ ОЉОљОъОдОбОЋОф ОъОЕОЋОЋОљОЋОф ОЊОЎОаОъОЎОЋОф. ОюОЊОЋОњОъОћ, ОљОЮ ОаОЎОДОЌ ОъОЏОЋОаОЎОф ОбОю ОЕОюОў ОЋОаОеОдОћ ОюОЉОаОЋОф ОъОЋОЊОю ОъОфОъОўОЎ ОЕОюОћ, ОаОЋОЏОю ОюОЉОЊОЋОД ОљОф ОћОАОцОД ОћОъОаОЋОб, ОДОЋОўОе ОћОњОюОњОюОЎОЮ ОЋОъОДОЊОъОЎ ОћОЌОЎОЏОЋОџ ОЕОюОћОЮ, ОъОАОф ОћОъОЏОЋОаОЎОф ОЋОЏОЋ', ОЋОюОћОдОЎОЉ ОљОф ОћОъОЕОфОаОЎОЮ ОћОюОюОЋ ОЉОъОЕОЋОЋОљОЋОф ОћОъОфОљОеОЋОф ОљОф ОфОаОЋОбОфОћ ОЕОю ОъОЏОЋОаОЎОф ОЋОюОДОЉОю ОъОЋОЊОю ОЕОю ОћОъОЏОЋОаОЎОф ОћОАОцОдОЎОцОЎОф ОЉОћ ОљОаОЋ ОъОЌОќОЎОДОЎОЮ. ОЕОЎОўОћ ОќОЋ ОаОДОеОљОф ОюОбОЎОфОЎОЮ "ОДОЋОцОАОћ ОюОЉОаОћ", ОъОЕОЋОЮ ОЕОюОбОЋОъОф ОДОЋОцОАОћ ОЕОЌОЋОеОћ ОљОаОЋ ОЎОЏОЋОюОЎОЮ ОюОеОљОЋОф ОъОћ ОаОъОдОљ ОЉОфОЋОЏОћ. ОЕОЎОўОћ ОќОЋ ОбОЕОЋОЎОћ ОюОћОЎОЋОф ОъОбОЕОЎОф ОбОЉОЋОе ОъОбОеОЏОЋОф ОцОЕОЋОўОЋОф, ОљОЋОюОЮ ОћОЋОцОЏОф ОцОЌОЋОф ОЋОцОЌОЋОф ОљОцОЕОеОЎОф ОЏОЏОю ОЕОћОъОбОеОЏОф ОъОЋОеОЏОЉОф ОЎОЋОфОе.
- ОќОЎОћОЋОЎ ОъОбОеОЏОЋОф (ОљОа'): ОЉОЕОЎОўОћ ОќОЋ ОъОЏОаОЎОАОЎОЮ ОюОъОбОеОЏОф ОЏОаОЎОАОЋОф ОъОАОЋОЎОъОф ОЋОъОЋОЊОЊОЎОЮ ОљОф ОћОЎОдОЎОљОЋОф ОЕОюОћ. ОЏОюОЎ ОћОќОЎОћОЋОЎ (ОюОеОЋОЉ ОфОЋОЏОаОЋОф) ОъОДОЉОюОЎОЮ ОљОф ОћОЏОаОЎОАОЋОф ОЋОћОЎОдОЎОљОЋОф ОЕОю ОћОъОбОеОЏОф ОЋОъОфОљОЎОъОЎОЮ ОљОф ОћОъОЋОЊОю ОћОъОфОъОўОЎ ОћОъОфОљОЎОЮ ОЉОЎОЋОфОе ОюОъОбОеОЏОф ОќОЋ. ОбОЉОЋОе ОЏОюОЎОЮ ОцОЕОЋОўОЎОЮ ОЎОЎОфОЏОЪ ОдОЋОеОџ ОюОћОњОЊОЎОе ОцОеОъОўОеОЎОЮ ОаОЋОАОцОЎОЮ ОЏОъОЋ ОАОЊОе ОћОъОбОеОЏОф (ОћОаОњОќОеОф ОћОњОЉОЋОћОћ ОЉОЎОЋОфОе ОЕОю ОћОъОЕОЋОЋОљОћ ОћОЊОЎОцОеОаОдОЎОљОюОЎОф / ОЊОеОњОф ОћОцОЋОюОЎОаОЋОЮ ОћОњОЉОЋОћОћ ОЉОЎОЋОфОе ОЉОцОЋОаОДОдОЎОЎОф ОћОфОъОАОЋОеОф), ОЋОЉОЏОюОЎОЮ ОъОфОДОЊОъОЎОЮ ОЎОЋОфОе ОћОфОЋОЏОаОћ ОфОќОћОћ ОњОЮ ОљОф ОдОЋОеОф ОћОъОбОеОЏОф ОЉОаОЋОАОБ ОюОъОДОЊОъОЎОЮ ОЕОюОћ. ОћОЎОфОеОЋОЪ ОЕОю ОЕОЎОўОћ ОќОЋ ОюОбОЋОъОф ОћОЕОЎОўОћ ОћОеОљОЕОЋОаОћ ОћОЎОљ ОћОЎОЏОЋОюОф ОюОДОЉОю ОъОЋОЊОю ОъОфОъОўОЎ ОъОЉОюОЎ ОЕОЎОћОЎОћ ОдОЋОеОџ ОюОћОЉОЎОЪ ОюОбОЋОъОД ОљОф ОћОЊОЎОаОъОЎОДОћ ОЕОю ОћОъОбОеОЏОф, ОЊОЉОе ОЕОбОЕОЋОЎ ОцОбОъОЎОЮ ОеОЉОЋОф ОюОћОЋОЋОф ОъОњОЉОюОћ ОбОю ОћОЎОЏОЋОюОф ОюОћОцОЎОД ОъОЋОЊОю. ОЉОЕОю ОЏОџ ОаОДОеОљОф ОюОбОЎОфОЎОЮ ОЕОЎОўОћ ОќОЋ "ОДОЋОцОАОћ ОЕОЌОЋОеОћ", ОЕОЏОЪ ОљОаОЋ ОъОфОЎОЎОЌОАОЎОЮ ОюОъОбОеОЏОф ОЏОљОю ОДОЋОцОАОћ ОЕОљОЎОаОаОЋ ОЎОЋОЊОбОЎОЮ ОъОћ ОаОъОдОљ ОЉОфОЋОЏОћ, ОЋОеОД ОъОбОЋОаОЎОЎОаОЎОЮ ОюОћОЉОЎОЪ ОљОф ОћОДОЕОе ОЉОЎОЪ ОћОЏОаОЎОАОћ ОюОЎОдОЎОљОћ ОЕОюОћ. ОюОбОЎОфОЎОЮ ОљОЋОцОЪ ОЉОаОЎОЎОф ОћОъОЋОЊОю ОЎОфОЋОљОе ОЏ"ОДОЋОцОАОћ ОљОцОЋОеОћ", ОћОъОфОљОе ОъОдОЉ ОЉОЎОаОЎОЎОЮ ОЉОЋ ОљОаОЋ ОъОЉОЎОаОЎОЮ ОљОф ОљОЋОцОЪ ОцОбОЋОюОфОћ ОЕОю ОЌОюОД ОъОћОъОбОеОЏОф ОљОЋОюОЮ ОъОЕОфОъОЕОЎОЮ ОЉОЏОюОЎ ОќОЎОћОЋОЎ ОбОю ОъОаОф ОюОћОЕОюОЎОЮ ОљОф ОћОЎОЊОб ОћОЌОАОе ОюОаОЋ ОюОњОЉОЎОћ.
ОеОљОЋ ОњОЮ
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ
ОћОбОеОЋОф ОЕОЋОюОЎОЎОЮ
- ^ Khaled Sailan and Klaus.Dieter Kuhnert, Modeling and design of cruise control system with feedforward for all terrian vehicles
- ^ Understanding PID Control, Part 1: What is PID Control? - YouTube, www.youtube.com
- ^ Techbriefs Media Group, The Modern Industrial Workhorse: PID Controllers, www.techbriefs.com (ОЉОљОаОњОюОЎОф)
- ^ Understanding PID Control, Part 4: A PID Tuning Guide - YouTube, www.youtube.com
- ^ Wayback Machine, web.archive.org, 2016-08-09
- ^ A Brief Building Automation History, web.archive.org, 2011-07-08
- ^ Brian Douglas - The step response
- ^ Brian Douglas - Introduction to System Stability and Control
- ^ Control Tutorials for MATLAB and Simulink - Introduction: PID Controller Design, ctms.engin.umich.edu
- ^ Systems Engineering, Part 1: What Is Systems Engineering?
- ^ Understanding PID Control, Part 4: A PID Tuning Guide
- ^ Stability of Closed Loop Control Systems
- ^ ОфОЋОеОф ОћОЉОДОеОћ/ОЕОЎОўОф ОюОЋОДОЋОА ОћОЕОЋОеОЕОЎОЮ РђЊ ОЋОЎОДОЎОАОцОе, ОЉОљОфОе he.wikibooks.org