תשעת הפרקים של אמנות המתמטיקה

תשעת הפרקים של אמנות המתמטיקה (סינית מסורתית: 九章算術, סינית מפושטת: 九章算术, פין-יין: Jiǔzhāng Suànshù, תעתיק עברי: גְ'יו גָא'נְג סוָּאן שוּ) הוא ספר מתמטיקה סיני שחובר בידי מספר דורות של מלומדים החל מהמאה ה-2 לפנה"ס ועד למאה ה-1 לספירה. הגישה המתמטית המגולמת ב"תשעת הפרקים של אמנות המתמטיקה" (להלן: "תשעת הפרקים") היא מציאת השיטות הכלליות ביותר לפתרון בעיות מעשיות. זוהי הגישה הסינית העתיקה האופיינית שהתרכזה במתמטיקה תכליתית, בניגוד לגישה המתמטית היוונית של אותה התקופה - זאת של יוון ההלניסטית - שהתמקדה בעיקר בהסקת משפטים מקבוצה נתונה של אקסיומות.

ראשי הפרקים בספר מתחילים, בדרך-כלל, עם הצהרה של בעיה, ממשיכים עם פתרון לבעיה ומסתיימים עם ניתוח התהליך שהוביל לפתרון זה.

היסטוריה

הכותרת המלאה הנוכחית של הספר מופיעה על שני לוחות ארד המתוארכים לשנת 179 לספירה, אך ישנן השערות שהספר הופיע אף בתקופה מוקדמת יותר בשם אחר[1].

כיום, רוב החוקרים סבורים שהמתמטיקה הסינית והמתמטיקה העתיקה של אגן הים התיכון התפתחו באופן עצמאי, פחות או יותר, עד לתקופה בה "תשעת הפרקים" לבש את צורתו הסופית. לכן יש אך מעט ערך היסטורי בהשערות על איזו מן התרבויות הייתה "יותר מתקדמת" בתקופת זמן כלשהי. אף-על-פי-כן, ניתן להעיר שהשיטה המתוארת בפרק 7 של הספר לא התגלתה באירופה עד למאה ה-13, והשיטה המתוארת בפרק 8 לא נמצאה לפני המאה ה-16. כמו כן, בין הכתבים ניתן למצוא הוכחה מתמטית למשפט פיתגורס[2]. ישנם גם עניינים מתמטיים של המתמטיקה המערבית הקדומה שלא נמצאו בסין העתיקה. ההשפעה של "תשעת הפרקים" סייעה רבות להתפתחותה של המתמטיקה העתיקה באזורי קוריאה ויפן. השפעתו של הספר על החשיבה המתמטית בסין ארכה זמן-רב, עד לתקופתה של שושלת צ'ינג.

בשנת 263, המתמטיקאי הסיני בן המאה ה-3 לִיאוּ הוּאַי כתב פרשנות מפורטת מאוד על הספר. הוא ניתח את התהליכים המתוארים ב"תשעת הפרקים" צעד אחר צעד, בצורה המכוונת לתת לקורא ביטחון מלא באמינותן - אם-כי, הוא לא הוכיח את אמיתותן של השיטות במובן האוקלידי הקלאסי. לפרשנות של לִיאוּ יש עניין מתמטי רב בפני-עצמה. לִיאוּ גם מזכיר את המתמטיקאים שקדמו לו, ז'אנג קאנג (נולד בין 165 לפנה"ס ל-142 לפנה"ס) וגֶנְג שאוּ-צ'אנג (נולד בין 75 לפנה"ס ל-49 לפנה"ס) (ראו גם הספירה הארמילרית), כאלו שסידרו את הפרקים של הספר בסדר הופעתם הנוכחי, וככותבי פרשנויות מוקדמות; אך רשימות מתקופת שושלת הָאן לא מזכירות שמות של מחברי פרשנויות כלשהם, וכאלה אינם מוזכרים עד למאה ה-3[3].

"תשעת הפרקים" נכתב בעילום שם ומקורותיו של הספר אינם ברורים. עד לשנים האחרונות לא היו כל ראיות מוצקות בדבר כתב מתמטי שקדם לו, אך פני-הדברים השתנו. ה"סוּאַן שוּ שוּה" (סינית מסורתית: 算數書), או "כתבים על התחשבנות", הוא חיבור מתמטי עתיק בן 7,000 תווים לערך, שנכתב על 190 רצועות במבוק. "כתבים על התחשבנות" התגלה לצד כתבים נוספים ב-1983 כשארכאולוגים פתחו קבר בזַ'אנְגגִ'יאָשַאן שבמחוז חוביי. מעדויות כתובות ידוע שקבר זה נסגר בשנת 186 לפנה"ס, בתחילת שושלת הָאן המערבית. ניתן בבירור לראות מספר דברים מקבילים בין שני הכתבים, אם כי יחסו של הספר ל"תשעת הפרקים" עדיין נדון על ידי חוקרים. לעומת זאת, ה"סואן שו שוה" הוא הרבה פחות עקבי מ"תשעת הפרקים", ונראה כי הוא מורכב מכמה חיבורים עצמאיים קצרים שנלקחו ממספר מקורות וצורפו יחדיו.

פרקי הספר

תוכנם של תשעת הפרקים הוא כדלהלן:

  1. 方田 פַאנְג טִיאַן - שדות מלבניים. בפרק זה, העוסק במדידת שטחיהם של שדות בצורות שונות, ישנם הסברים על ביצוע ארבע פעולות החשבון על שברים, כמו גם את האלגוריתם האוקלידי למציאת מחלק משותף מקסימלי.
  2. 粟米 סוּ מִי - דֹחַן ואורז. בפרק השני, העוסק בסחר ותמחור טובין, מובאות דוגמאות לשימוש בחוקי הפרופורציות והאחוזים.
  3. 衰分 קוּאַי פֶן - חלוקה פרופורציונלית. הפרק עוסק בחלוקות של סחורה וכסף. הפרק מתאר שימוש בחוקי פרופורציות, הן ישרות והן הפוכות, ואף שימוש בטורים חשבוניים והנדסיים.
  4. 少廣 שֵאוֹ גוּאַנְג - הרוחב הפחוּת. הפרק הרביעי עוסק בבעיות בהן ישנה תלות בין אורך לשטח ועוסק ביישומים של נושאים כגון שברי יחידה ושורשים מסדר שני ושלישי, ובמציאת השטח והנפח של מעגל וכדור. בפרק זה ניתן למצוא את רעיון הגבול והאינפיניטסימל[4].
  5. 商功 שַאנְג גוֹנְג - ייעוץ על עבודות. פרק זה עוסק בהנדסה אזרחית ובנושאים של הנדסת המרחב, כגון מציאת הנפח של גופים מצורות שונות.
  6. 均輸 ג'וּן שוּ - מיסוי הוגן. הפרק עוסק בבעיות מתקדמות יותר המשלבות נושאים כמו קצב ופרופורציה.
  7. 盈不足 יִינְג בּוּ זוּ - עודף וגרעון. הפרק השביעי עוסק בפתירת בעיות ליניאריות באמצעות השיטה שלימים תיקרא False position method או Regula falsi method, במתמטיקה המערבית.
  8. 方程 פַאנְג צֵ'נְג - המערך המלבני. פרק זה ממשיך את הפרק השביעי ודן בשיטות נוספות לפתרון בעיות ליניאריות בכמה משתנים. הספר מציג מספר שיטות הדומות לאלימינציית גאוס-ג'ורדן המודרנית.
  9. 勾股 גוּאַי גוּ - בסיס וגובה. הפרק התשיעי עוסק במשולשים ישרי זווית וכולל יישומים של מה שידוע במערב כמשפט פיתגורס, שלשות פיתגוראיות וחפיפת משולשים. כמו כן, ניתן למצוא בפרק זה משוואות ריבועיות ואת פתרונן באמצעות האלגוריתם הסיני להוצאת שורש ריבועי, ולא באמצעים אלגבריים.

תרגומים

עיון, מחקר ותרגום מלא לאנגלית של "תשעת הפרקים של אמנות המתמטיקה" ושל הפרשנות של לִיאוּ הוּאַי יצא בהוצאת Oxford בשנת 1999, בעריכתו של Shen Kangshen (עורך ראשי), תחת השם ‎"The Nine Chapters on the Mathematical Art: Companion and Commentary", ISBN 0-19-853936-3.‎.

כמו כן, בשנת 2004 יצא לאור תרגום לצרפתית המכיל גם נספחים מפורטים שנכתבו בידי חוקרים רבים, מהדורה מדעית של הטקסט הסיני והפרשנות של ליאו הואי. Chemla, Karine, and Shuchun Guo. 2004. Les neuf chapitres: le classique mathématique de la Chine ancienne et ses commentaires. Paris: Dunod.‎.

ראו גם

לקריאה נוספת

  • Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.

קישורים חיצוניים

ויקישיתוף מדיה וקבצים בנושא תשעת הפרקים של אמנות המתמטיקה בוויקישיתוף

הערות שוליים

  1. ^ Needham, Volume 3, 24-25.
  2. ^ Needham, Volume 3, 22.
  3. ^ Needham, Volume 3, 24.
  4. ^ [1]

Read other articles:

Dani Hernández

Dani Hernández Informasi pribadiNama lengkap Daniel Hernández SantosTanggal lahir 21 Oktober 1985 (umur 38)Tempat lahir Caracas, VenezuelaTinggi 1,96 m (6 ft 5 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini TenerifeNomor 25Karier junior TenerifeKarier senior*Tahun Tim Tampil (Gol)2002–2003 Rayo Majadahonda 2003–2004 Guadalajara 2004–2005 Collado Villaba 2005–2007 Real Madrid C 1 (0)2007–2008 Rayo B 28 (0)2007–2008 Rayo Vallecano 0 (0)2008–2009...

 

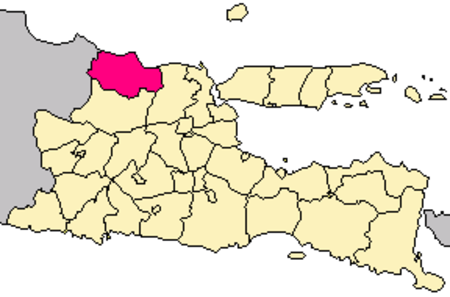
Daftar kecamatan dan kelurahan di Kabupaten Tuban

Peta lokasi Kabupaten Tuban Berikut adalah daftar kecamatan dan kelurahan/desa di Kabupaten Tuban, Provinsi Jawa Timur, Indonesia. Kabupaten Tuban terdiri dari 20 kecamatan, 17 kelurahan, dan 311 desa (dari total 666 kecamatan, 777 kelurahan, dan 7.724 desa di Jawa Timur). Pada tahun 2017, jumlah penduduknya mencapai 1.189.855 jiwa dengan luas wilayah 1.834,15 km² dan sebaran penduduk 648 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Tuban, adalah sebagai berik...

 

Ethylnorepinephrine

Chemical compound EthylnorepinephrineClinical dataOther namesβ,3,4-trihydroxy-N-ethyl-2-phenylethylamineATC codeNoneLegal statusLegal status In general: ℞ (Prescription only) Identifiers IUPAC name 4-(2-amino-1-hydroxybutyl)benzene-1,2-diol CAS Number536-24-3 NPubChem CID18538ChemSpider17508 YUNIIM6AY4VCZ0AChEMBLChEMBL31159 YCompTox Dashboard (EPA)DTXSID10968369 Chemical and physical dataFormulaC10H15NO3Molar mass197.234 g·mol−13D model (JSmol)Interactive i...

Reinado Internacional del Café

Reinado Internacional del CaféReinado Internacional del Café 2008, Jessica Jordan dari BoliviaTanggal pendirian1957TipeKontes kecantikanKantor pusatManizalesLokasi KolombiaBahasa resmi Bahasa Inggris Kontes kecantikan Reinado Internacional del Café (Bahasa Inggris: International Queen of Coffee; Bahasa Indonesia: Ratu Kopi Internasional), merupakan kontes kecantikan bagi negara-negara penghasil kopi di seluruh dunia. Secara internasional diluncurkan sebagai Reinado Continental del Caf...

 

The Jackal (soundtrack)

1997 soundtrack album by Various ArtistsThe JackalSoundtrack album by Various ArtistsReleased28 October 1997GenreBig beat, electronica, breakbeat, trip hop, alternative rockLabelMCA Records The Jackal soundtrack features music from and inspired by the 1997 remake of the film of the same name. It was released in 1997 on MCA Records. Track listing Going Out of My Head - Fatboy Slim Poison - The Prodigy Superpredators (Metal Postcard) - Massive Attack (based on samples of Siouxsie and th...

 

Pantao Ragat

Municipality in Lanao del Norte, Philippines Municipality in Northern Mindanao, PhilippinesPantao RagatMunicipalityMunicipality of Pantao Ragat SealMap of Lanao del Norte with Pantao Ragat highlightedOpenStreetMapPantao RagatLocation within the PhilippinesCoordinates: 8°03′N 124°09′E / 8.05°N 124.15°E / 8.05; 124.15CountryPhilippinesRegionNorthern MindanaoProvinceLanao del NorteDistrict 2nd districtFoundedJune 1, 1966Barangays20 (see Barangays)Government ...

Temperate broadleaf and mixed forests

Biome Extent of temperate broadleaf and mixed forests An example of temperate broadleaf and mixed forest in La Mauricie National Park, Quebec. Temperate broadleaf and mixed forest is a temperate climate terrestrial habitat type defined by the World Wide Fund for Nature, with broadleaf tree ecoregions, and with conifer and broadleaf tree mixed coniferous forest ecoregions.[1] These forests are richest and most distinctive in central China and eastern North America, with some other glob...

 

Lingua pitcairnese

Questa voce o sezione sull'argomento lingue non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: voce priva di fonti a supporto. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. PitcairnesePitkernParlato in Isole Pitcairn LocutoriTotale50 TassonomiaFilogenesiLingue creole Creole inglesi  Creole del Pacifico   Pitcairne...

 

华盛顿州

  关于与「华盛顿州」標題相近或相同的条目页，請見「华盛顿」。   此條目介紹的是美國西北部太平洋沿岸的州。关于与之同名的美国首都所在地，请见「華盛頓哥伦比亚特区」。 此條目需要擴充。 (2007年9月26日)请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 华盛顿州 美國联邦州State of Washington...

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

 

Beach golf

Golf-based beach sport Beach Golf event 2002 Special Beach Golf Ball Beach golf is a variation of golf mainly played on sandy beaches. It was devised with the aim of a simplified and more accessible version of golf. The game is played along a distance of about 2 kilometres (1.2 miles) on which the players, two per team, with as few strokes as possible, have to reach the final hole, hitting a soft polyurethane ball with a classic golf club. History Beach golf was created in Pescara, Italy in 1...

 

Peter the Aleut

Christian martyr and saint Saint Peter the AleutIcon of St. Peter the AleutMartyr of San Francisco and Protomartyr of AmericaBornCungagnaqc. 1800[citation needed]Died1815Venerated inEastern Orthodox ChurchCanonized1980 by Orthodox Church in AmericaFeastSeptember 24; December 12Attributesportrayed as an Aleut youth, wearing a traditional gut parka[1] Cungagnaq (Russian: Чукагнак, romanized: Chukagnak; date of birth unknown - d. 1815) is venerated as a martyr an...

Julian Casablancas

American singer (born 1978) Julian CasablancasCasablancas in 2022BornJulian Fernando Casablancas (1978-08-23) August 23, 1978 (age 45)New York City, U.S.OccupationsSingersongwritermusicianYears active1998–presentSpouse Juliet Joslin ​ ​(m. 2005; div. 2019)​Children2ParentJohn Casablancas (father)Musical careerGenresIndie rockpost-punk revivalgarage rock revivalnew waveexperimental rockneo-psychedeliaMember ofThe StrokesThe VoidzWebsi...

 

متلازمة وولف -باركنسون -وايت

متلازمة وولف -باركنسون -وايت موجة دلتا مميزة في شخص يعانون من متلازمة وولف باركنسون وايت. .موجة دلتا مميزة في شخص يعانون من متلازمة وولف باركنسون وايت. . معلومات عامة الاختصاص طب القلب  من أنواع المتلازمة السابقة للإثارة،  وإحصار القلب،  واضطراب جيني،  ومرض  الإ...

 

伊凡一世

此條目没有列出任何参考或来源。 (2012年2月7日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 伊凡一世 伊凡一世·丹尼洛维奇（钱袋）（Ива́н I Дани́лович Калита́，1288年—1340年3月31日），是莫斯科大公（约1325年－1340年3月31日在位），亚历山大·涅夫斯基幼子丹尼尔·亚历山德罗维奇�...

قائمة مدن أوكلاهوما

هذه قائمة مدن ولاية أوكلاهوما في الولايات المتحدة، والتي يسكنها أكثر من 10000 نسمة حسب إحصاء 2010.   †  مقر المقاطعة   ††  عاصمة ومقر المقاطعة — أوكلاهوما سيتي (أوكلاهوما), عاصمة أوكلاهوما تلسا (أوكلاهوما) ترتيب 2012 المدينة تقدير 2012[1] إحصاء 2010[2] التغيير ال...

 

Diakonie Deutschland

Logo The Diakonie Deutschland is a charitable organization of Protestant churches in Germany (Protestant Church in Germany), Austria as well as numerous free churches. Its Roman Catholic equivalent is the Caritas. vteHumanitarian partners of the European Commission Humanitarian partners DG ECHO NGOsInternational Action Against Hunger (France, Spain) ADRA (Czech Republic, Denmark, Germany) CARE International (Austria, Denmark, France, Germany, Netherlands, Norway) Caritas Internationalis (Aust...

 

貴景勝貴信

貴景勝 貴信 基礎情報四股名 佐藤 貴信→貴景勝 光信→貴景勝 貴信本名 佐藤 貴信愛称 タカノブ[1]、ケーショー、芦屋の暴れん坊[2]、貴乃花親方の秘蔵っ子[3]生年月日 1996年8月5日　(28歳)出身 兵庫県芦屋市身長 175cm体重 165kgBMI 53.88所属部屋 貴乃花部屋→千賀ノ浦部屋→常盤山部屋得意技 突き、押し成績現在の番付 西関脇2最高位 東大関生涯戦歴 441勝2...

Академия труда и социальных отношений

Академия труда и социальных отношений(АТиСО) Прежнее название Высшая школа профсоюзного движения ВЦСПС им. Н. М. Шверника Год основания 1919 год Ректор Нина Николаевна Кузьмина Бакалавриат Есть Магистратура Есть Аспирантура Есть Юридический адрес 119454, Москва, ул. Лобачевс...

 

三菱重工業

三菱グループ > 三菱重工業 三菱重工業株式会社Mitsubishi Heavy Industries, Ltd. 丸の内二重橋ビル種類 株式会社機関設計 監査等委員会設置会社[1]市場情報 東証プライム 70111950年5月29日上場 名証プレミア 70111950年8月29日上場 福証 70111949年7月1日上場 札証 70111950年6月1日上場 略称 三菱重工・三重・重工・MHI本社所在地 日本〒100-8332東京都千代田区丸の内三丁目2番3号...