ОъОАОюОЋОю ОЏОЉОЎОЊОфОЎ
| ||||||
Read other articles:

Aghire┼Ъu EgeresDesaReruntuhan Kastil Aghire┼ЪuLocation of the settlement on County mapLua error in Modul:Location_map at line 425: Kesalahan format nilai koordinat.Koordinat: Lua error in package.lua at line 80: module 'Module:ISO 3166/data/RO' not found.Country RumaniaCountyCluj CountyStatusCommune (Comun─Ѓ)Settled1263Commune seatAghire┼ЪuVillagesAghire┼Ъu, Aghire┼Ъu-Fabrici, Arghi┼Ъu, B─Ѓgara, D├бncu, Dorol┼Бu, Inucu, Leghia, Mac─Ѓu, Ticu, Ticu-ColoniePemerintahan Рђб MayorL...
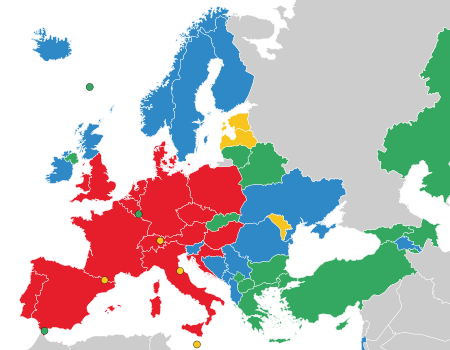
Liga Negara UEFA 2022РђЊ2023Informasi turnamenJadwalpenyelenggaraanFase liga:1 Juni РђЊ 27 September 2022Babak final:14РђЊ18 Juni 2023Perebutan tempat degradasi:21РђЊ26 Maret 2024Jumlahtim peserta55Hasil turnamenJuara Spanyol (gelar ke-1)Tempat kedua KroasiaTempat ketiga ItaliaTempat keempat BelandaStatistik turnamenJumlahpertandingan160Jumlah gol423 (2,64 per pertandingan)Jumlahpenonton3.219.559 (20.122 per pertandingan)Pencetak golterbanyak Erling Haaland Aleks...

Halaman ini berisi artikel tentang permainan video. Untuk kegunaan lain, lihat Psychonaut (disambiguasi). Psychonauts Publikasi 19 April 2005 Microsoft WindowsNA: 19 April 2005EU: 10 Februari 2006 XboxNA: 20 April 2005EU: 10 Februari 2006 PlayStation 2NA: 22 Juni 2005EU: 10 Februari 2006 PlayStation 4WW: 7 Juni 2016 GenrePlatformBahasa Daftar Inggris, Jerman dan Prancis 60 Karakteristik teknisPlatformXbox, Windows, PlayStation 2, Linux, Xbox 360, macOS, PlayStation 4 dan PlayStation 3 ModePer...

Piala SoeratinLogo piala soeratinPenyelenggaraPSSIMulai digelar1965; 59 tahun lalu (1965)WilayahIndonesiaJumlah timNasional32 (U-17)27 (U-15)Juara bertahanU-18/U-17: Persikasi Bekasi (gelar ke-4)U-15: ASIOP FC (gelar pertama)Tim tersuksesU-18/U-17 Persikasi Bekasi (4 gelar)Persijap JeparaPersebaya Surabaya(masing-masing 3 gelar)U-15Persib BandungPSSA Asahan(masing masing 7 gelar)Televisi penyiarMola Piala Soeratin 2023 Piala Soeratin adalah sebuah turnamen kompetisi sepak bola di Indones...

F├Еd├Еration Internationale F├ЕlineLogo FIFeSingkatanFIFeTanggal pendirian1949Wilayah layanan Seluruh negaraSitus webwww.fifeweb.org F├Еd├Еration Internationale F├Еline (atau FIFe, Indonesia: Federasi Kucing Internasional) adalah federasi pendaftaran dan pengakuan ras kucing. FIFe diatur ke dalam sub-federasi nasional, misalnya Felis Britannica di Inggris, yang menangani pendaftaran silsilah, kontes kucing dan penghargaan di setiap negara. Sejarah FIFe didirikan oleh Marguerite Ravel pada tah...

пг┘ЁпД┘ё п▓┘іп»пД┘є ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» 28 пБпеп▒┘і┘ё 1955 (пД┘ёп╣┘Ёп▒ 68 п│┘єпЕ)пД┘ёпгп▓пДпдп▒пї пД┘ёпгп▓пДпдп▒ пД┘ёпи┘ѕ┘ё 1.80 ┘Ё (5 ┘ѓп»┘Ё 11 пе┘ѕпхпЕ) ┘Ёп▒┘Ѓп▓ пД┘ё┘ёп╣пе ┘Ё┘ЄпДпг┘Ё пД┘ёпг┘єп│┘іпЕ пД┘ёпгп▓пДпдп▒ ┘Ёп│┘іп▒пЕ пД┘ёп┤пепДпе п│┘є┘ѕпДпф ┘Ђп▒┘і┘ѓ 1967РђЊ1972 пДпфпГпДп» пД┘ёпгп▓пДпдп▒ пД┘ё┘Ёп│┘іп▒пЕ пД┘ёпДпГпфп▒пД┘Ђ┘іпЕ1 п│┘є┘ѕпДпф ┘Ђп▒┘і┘ѓ ┘Ё. (┘Є┘ђ.) 1967РђЊ1972 пДпфпГпДп» пД┘ёпгп▓пДпдп▒ 0 (0) 1976РђЊ1977 AS Corbeil-Essonnes 1977РђЊ1978...

American conspiracy theory and political movement QAnon flag featuring an American flag defaced with the Q logo alongside the slogan Where we go one, we go all, at a Second Amendment rally in Richmond, 2020 QAnon[a] (/╦ѕkju╦љ╔Ўn╔њn/ KYOO-╔Ў-non or /╦ѕkju╦љ├дn╔њn/ KYOO-an-on) is a far-right American political conspiracy theory and political movement that originated in 2017.[1][2] QAnon centers on fabricated claims made by an anonymous individual or individuals known as ...

Business information kept secret to gain or maintain a competitive advantage For other uses, see Trade secret (disambiguation). This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2023) Intellectual property Authors' rights Copyleft Copyright Database right Farmers' rights Geographical indication Indigenous intellectual property Industrial desi...

Jacek Rostowski Jacek Rostowski en 2009. Fonctions Vice-pr├Еsident du Conseil des ministres polonais 25 f├Еvrier РђЊ 21 novembre 2013(8 mois et 27 jours) Pr├Еsident du Conseil Donald Tusk Gouvernement Tusk II Successeur El┼╝bieta Bie┼ёkowska D├Еput├Е ├а la Di├еte 8 novembre 2011 РђЊ 11 novembre 2015(4 ans et 3 jours) ├Ѕlection 9 octobre 2011 L├Еgislature VIIe Groupe politique PO Ministre des Finances 16 novembre 2007 РђЊ 21 novembre 2013(6 ans et 5 jours) Pr├Еsi...

лБ ЛЇЛѓлЙл│лЙ ЛѓлхЛђл╝лИлйл░ ЛЂЛЃЛЅлхЛЂЛѓл▓ЛЃЛјЛѓ лИ л┤ЛђЛЃл│лИлх лилйл░ЛЄлхлйлИЛЈ, ЛЂл╝. лАлхл▓лхЛђЛЂЛѓл░л╗Лї (лилйл░ЛЄлхлйлИЛЈ). лЪлљлъ ┬ФлАлхл▓лхЛђЛЂЛѓл░л╗Лї┬╗ лблИл┐ лЪЛЃл▒л╗лИЛЄлйл░ЛЈ л║лЙл╝л┐л░лйлИЛЈ лЏлИЛЂЛѓлИлйл│ лйл░ л▒лИЛђлХлх MCX: CHMFLSE: SVST[1] лъЛЂлйлЙл▓л░лйлИлх 1955 лал░ЛЂл┐лЙл╗лЙлХлхлйлИлх лалЙЛЂЛЂлИЛЈ: лДлхЛђлхл┐лЙл▓лхЛє, лњлЙл╗лЙл│лЙл┤ЛЂл║л░ЛЈ лЙл▒л╗л░ЛЂЛѓЛї лџл╗ЛјЛЄлхл▓ЛІлх ЛёлИл│ЛЃЛђЛІ лљл╗лхл║ЛЂлхл╣ люлЙЛђл┤л░ЛѕлЙл▓ (лЪЛђлхл┤ЛЂлхл┤л░Лѓлхл╗Лї ЛЂлЙл▓лхЛѓл░ л┤...

Fictional cartoon character Fictional character Dick DastardlyWacky Races characterDick Dastardly as seen in Wacky RacesFirst appearanceSee-Saw To Arkansas (1968)Created byWilliam HannaJoseph BarberaPortrayed byPorter Flynn (2013)Voiced byPaul Winchell (1968РђЊ1991)Malcolm McNeill (Spin a Magic Tune)[1][2]Michael Bell (1990)Rob Paulsen (1991)Jim Cummings (2000РђЊ2008)Jeff Bergman (Cartoon Network)Trey Parker (South Park)Eric Bauza (Uncle Grandpa)Peter Woodward (2017РђЊ2019)Jas...

2015 2028 ├Ѕlections d├Еpartementales de 2021 dans le Lot 34 si├еges au sein du Conseil d├Еpartemental du Lot les 20 et 27 juin 2021 Type dРђЎ├Еlection ├Ѕlections d├Еpartementales Campagne Du 31 mai 2021 au 18 juin 2021 Du 21 juin 2021 au 25 juin 2021 Corps ├Еlectoral et r├Еsultats Population 173 828 Inscrits 136 740 Votants au 1er tour 59 960 43,85 % 15,6 Votes exprim├Еs au 1er tour 53 586 Votes blancs au 1er tour 3 836 Votes nuls au 1er tou...

Motorway in the Netherlands This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: A7 motorway Netherlands РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (November 2016) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in Dutch. Cli...
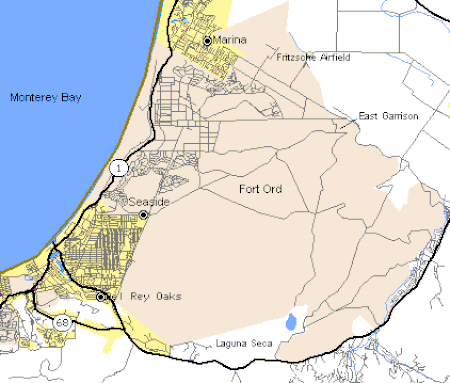
Former U.S. Army Fort in California This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fort Ord РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (December 2014) (Learn how and when to remove this message) Fort Ord National MonumentMonterey Bay area, California Abandoned Army barracks at Fort OrdFort Ord National M...

пг┘ѕпДп▓ п│┘Ђп▒ ┘є┘іпгп▒┘іпД┘ёп║┘ёпД┘Ђ пД┘ёпБ┘ЁпД┘Ё┘і ┘ё┘ёпг┘ѕпДп▓ пД┘ё┘є┘іпгп▒┘і┘Ёп╣┘ё┘ѕ┘ЁпДпф п╣пД┘ЁпЕ┘є┘ѕп╣ пД┘ё┘Ёп│пф┘єп» пг┘ѕпДп▓ п│┘Ђп▒пхпДп»п▒ п╣┘є пД┘ё┘є┘іпгп▒пхпД┘ёпГ ┘Ђ┘і пД┘ё┘є┘іпгп▒┘Ёпфпи┘ёпепДпф пД┘ёпДп│пфпГ┘ѓпД┘ѓ пД┘ё┘Ё┘ѕпДпи┘єпЕ пД┘ё┘є┘іпгп▒┘іпЕпД┘ёпД┘єпф┘ЄпДпА ┘ЁпГп»п»пфп╣п»┘і┘ё - пфп╣п»┘і┘ё ┘Ёпхп»п▒┘і - пфп╣п»┘і┘ё ┘ѕ┘і┘Ѓ┘і пе┘іпД┘єпДпф пг┘ѕпДп▓ пД┘ёп│┘Ђп▒ пД┘ё┘є┘іпгп▒┘і ┘Є┘ѕ ┘ѕпФ┘і┘ѓпЕ п▒п│┘Ё┘іпЕ пфпхп»п▒ ┘ё┘Ё┘ѕпДпи┘є┘і пД┘ё┘є┘іпгп▒пї ┘ё┘ёп│┘Ђп▒ пД┘ёп»┘ѕ┘ё┘і. ┘ѕпфпипеп╣...

тє░С║║IcemanсђіAll-New X-MenсђІ#31уџётє░С║║ућ▒Тќ»тюќуѕЙуЅ╣┬иУњЎтФЕ№╝ѕУІ▒У»Г№╝џStuart Immonen№╝ЅсђЂжЪІтЙи┬ижд«┬иТа╝тІъти┤тѓЉ№╝ѕУІ▒У»Г№╝џWade Von Grawbadger№╝ЅтњїждгуЅ╣┬иТа╝ТІЅУЦ┐С║ъу╣фУБйСйютЊЂС┐АТЂ»ждќТгАуЎ╗та┤сђіUncanny X-MenсђІугг1ТюЪ№╝ѕ1963т╣┤9Тюѕ№╝ЅтѕЏСйюУђЁтЈ▓СИ╣┬иТЮјтѓЉтЁІ┬иуДЉТ»ћТЋЁС║ІС┐АТЂ»уюЪтљЇуЙЁС╝»уЅ╣┬иУи»ТўЊТќ»┬исђїж«ЉТ»ћсђЇ┬иТЮюуЉътЁІ№╝ѕRobert Louis Bobby Drake№╝ЅуДЇу▒╗У«іуе«С║║ТЅђт▒ътЏбжўЪXТѕ░УГдXтЏатГљ№╝ѕУІ▒У»Г№╝џX-Factor (comics)№╝ЅтєаУ╗Ї№╝ѕУІ▒У»Г№╝џChampions (1975 team)№╝Ѕ№┐й...

Athletic teams representing Southern Arkansas University Southern Arkansas MuleridersUniversitySouthern Arkansas UniversityConferenceGreat American ConferenceNCAADivision IIAthletic directorSteve BrowningLocationMagnolia, ArkansasVarsity teams16 (8 men's, 8 women's)Football stadiumWilkins Stadium (capacity: 6,000)Basketball arenaW.T. Watson Athletic Center (capacity: 2,500)Baseball stadiumWalker Stadium at Goodheart Field (capacity: 1,000)MascotMolly AnnNicknameMuleriders/Lady MuleridersFigh...

Pour un article plus g├Еn├Еral, voir Dioc├еse de Saint-Papoul. Carte du dioc├еse de Saint-Papoul en 1781. Ancien palais ├Еpiscopal de Saint-Papoul. Voici la Liste des ├Еv├фques de Saint-Papoul. Le dioc├еse de Saint-Papoul, ├Еrig├Е en 1317 et supprim├Е en 1801 ├Еtait situ├Е dans l'actuel d├Еpartement de l'Aude. Moyen ├ѓge XIVe si├еcle Bernard de La Tour, du 11 juillet 1317 au 27 d├Еcembre 1317 Raymond de Mostu├еjouls 1319-1329, transf├Еr├Е de Saint-Flour (bulle du 16 avril 1319), cardina...

пД┘ёп»┘ѕп▒┘і пД┘ё┘Ѓп▒┘ѕпДпф┘і пД┘ё┘Ё┘ЁпфпДп▓ 2010РђЊ11 пф┘ЂпДпх┘і┘ё пД┘ё┘Ё┘ѕп│┘Ё пД┘ёп»┘ѕп▒┘і пД┘ё┘Ѓп▒┘ѕпДпф┘і пД┘ё┘Ё┘ЁпфпДп▓ пД┘ё┘єп│п«пЕ 20 пД┘ёпе┘ёп» ┘Ѓп▒┘ѕпДпф┘іпД пД┘ёпфпДп▒┘іп« пеп»пД┘іпЕ:24 ┘і┘ѕ┘ё┘і┘ѕ 2010 ┘є┘ЄпД┘іпЕ:21 ┘ЁпД┘і┘ѕ 2011 пД┘ё┘Ё┘єпИ┘Ё пДпфпГпДп» ┘Ѓп▒┘ѕпДпф┘іпД ┘ё┘Ѓп▒пЕ пД┘ё┘ѓп»┘Ё пД┘ёпепи┘ё п»┘і┘єпД┘Ё┘ѕ п▓п║п▒пе ┘ЁпепДп▒┘іпДпф ┘Ё┘ёп╣┘ѕпепЕ 240 п╣п»п» пД┘ё┘Ёп┤пДп▒┘Ѓ┘і┘є 16 пД┘ёп»┘ѕп▒┘і пД┘ё┘Ѓп▒┘ѕпДпф┘і пД┘ё┘Ё┘ЁпфпДп▓ 2...

Giorgio MichettiNascitaFrancavilla al Mare, 29 maggio 1888 MorteRoma, 4 febbraio 1966 Dati militariPaese servito Italia Forza armataRegio Esercito CorpoCorpo aeronautico militare Reparto43┬ф Squadriglia Caccia76┬ф Squadriglia Caccia GradoTenente GuerrePrima guerra mondiale DecorazioniMedaglia d'argento al valor militare (2) wwiaviation.com[1] voci di militari presenti su Wikipedia Manuale Giorgio Michetti (Francavilla al Mare, 29 maggio 1888 РђЊ Roma, 4 febbraio 1966...


