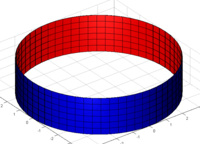
כיסוי האוריינטציות
| ||||||||||||||||||||||
Read other articles:

Ini adalah sebuah nama Islandia. Nama terakhirnya adalah sebuah nama keluarga, namun tokoh ini biasa disebut dengan nama panggilannya, Baltasar. Baltasar KormákurBaltasar Kormákur di FFIKV ke-42, 2007LahirBaltasar Kormákur Samper27 Februari 1966 (umur 58)Reykjavík, IslandiaPekerjaanAktor, sutradara, produserTahun aktif1992–sekarang Baltasar Kormákur Samper (kelahiran 27 Februari 1966) adalah seorang aktor, sutradara film dan teater Islandia. Ia dikenal secara profesional seba...

Questa voce sull'argomento calciatori ciprioti è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Giōrgos Savvidīs Nazionalità Cipro Altezza 181 cm Calcio Ruolo Attaccante Termine carriera 1996 - giocatore2008 - allenatore Carriera Squadre di club1 1981-1987 Omonia190 (101)1987-1992 AEK Atene135 (33)1992-1996 Omonia93 (19) Nazionale 1982-1995 Cipro46 (2) Carriera da allenatore 1999...

English cricketer George LohmannLohmann c. 1895Personal informationFull nameGeorge Alfred LohmannBorn(1865-06-02)2 June 1865Kensington, Middlesex, EnglandDied1 December 1901(1901-12-01) (aged 36)Worcester, British Cape ColonyBattingRight-handedBowlingRight arm medium-fastInternational information National sideEnglandTest debut (cap 51)5 July 1886 v AustraliaLast Test24 June 1896 v Australia Domestic team information YearsTeam1884–1896Surrey1894–1897W...

Eighth meeting of the G-20 heads of government 2013 G20 Russia summitLogo of the G20 Russia 2013 summitHost countryRussiaDate5–6 SeptemberMottoBoosting Economic Growth and Job CreationVenue(s)Constantine PalaceCitiesSaint PetersburgParticipantsG20 members Guest invitees: Spain, Kazakhstan, Singapore; ASEAN, African Union, NEPADFollows2012 G20 Los Cabos summitPrecedes2014 G20 Brisbane summitWebsiteRussia G20 The 2013 G20 Saint Petersburg summit was the eighth meeting of the G20 heads of gove...

Fictional world This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is like...

La rilevanza enciclopedica di questa voce o sezione sull'argomento Marvel Comics è stata messa in dubbio. Motivo: voce priva di fonti terze che dimostrino una rilevanza del personaggio al di fuori delle opere Puoi aiutare aggiungendo informazioni verificabili e non evasive sulla rilevanza, citando fonti attendibili di terze parti e partecipando alla discussione. Se ritieni la voce non enciclopedica, puoi proporne la cancellazione. Segui i suggerimenti del progetto di riferimento. Per i...

Il collegioLogo del programma televisivoPaeseItalia Anno2017 – in produzione Generedocu-reality Edizioni8 Puntate49 (al 5 novembre 2023) Durata120-130 min (2017-2019)130-150 min (2020-2022)90-120 min (dal 2023) Lingua originaleitaliano RealizzazioneNarratoreGiancarlo Magalli (2017-2019, 2020-2021)Eric Alexander e Simona Ventura (2019)Nino Frassica (2022)Stefano De Martino (dal 2023) RegiaFederico Favaron (notturna), Fabrizio De Plano, Fabio Calvi, Giam Paolo Marconato Aiuto regiaFabrizio De...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

20th and 21st-century Norwegian bishop The Right ReverendFinn WagleBishop Emeritus of NidarosFormer Primate of the Church of NorwayFinn WagleChurchChurch of NorwayIn office1991–2008PredecessorKristen Kyrre BremerSuccessorTor SingsaasOrdersConsecration28 April 1991by Andreas AarflotPersonal detailsBorn (1941-06-19) 19 June 1941 (age 82)Oslo, NorwayDenominationLutheranOccupationBishopEducationcand.theol. (1968)Alma materMF Norwegian School of Theology Finn Wagle (born 19 June 1941) ...

Bandar Udara Frans KaisiepoFrans Kaisiepo AirportIATA: BIKICAO: WABBInformasiJenisPublikPemilikPT Aviasi Pariwisata Indonesia (Persero)PengelolaPT Angkasa Pura I[1]MelayaniPulau BiakLokasiBiak, Kabupaten Biak Numfor, Papua, IndonesiaZona waktuWIT (UTC+09:00)Ketinggian dpl14 mdplKoordinat01°11′24″S 136°06′27″E / 1.19000°S 136.10750°E / -1.19000; 136.10750Koordinat: 01°11′24″S 136°06′27″E / 1.19000°S 136.10750°E&#...

Bus manufacturer based in the United Kingdom This article is about the Scottish bus manufacturer. For the English football player, see Dennis Alexander. Not to be confused with Denis Alexander or Denis Alexander, 6th Earl of Caledon. Alexander DennisCompany typeSubsidiaryIndustryBus manufacturingPredecessorTransBus InternationalFounded2004; 20 years ago (2004)HeadquartersLarbert, ScotlandKey peoplePaul Davies, President & Managing Director[1]ProductsBusesRevenue...

هذه المقالة هي تمهيدٌ ومدخلٌ غير مُفصل إلى الموضوع. من أجل المقالة الموسوعيّة، طالع تطور. جزء من سلسلة مقالات حولالتطور مواضيع رئيسية مدخل إلى التطور نظرية التطور سلف مشترك أدلة السلف المشترك عمليات ونتائج وراثيات سكانية تنوع جيني طفرة تكيف اصطفاء طبيعي انحراف وراثي انسي...

Compatibility of anarchism with capitalism and possible resulting problems Part of a series onAnarchism History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Free-market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Agorism Illegalism Insurrectionary Communization Expropriative Pacifist Platformism Especifismo...

Katedral Iskitim Eparki Iskitim adalah sebuah eparki Gereja Ortodoks Rusia yang terletak di Iskitim, Federasi Rusia. Eparki tersebut didirikan pada 2011.[1] Referensi ^ http://www.patriarchia.ru/db/text/1909396.html lbsKeuskupan Gereja Ortodoks RusiaPatriark MoskwaEparki di Rusia Abakan dan Khakassia Akhtubinsk Alapayevsk Alatyr Alexdanrov Almetyevsk Amur Anadyr Ardatov Arkhangelsk Armavir Arsenyev Astrakhan Balashov Barnaul Barysh Belgorod Belyov Bezhetsk Birobidzhan Birsk Biysk Blag...

Moritz HeyerNazionalità Germania Altezza184 cm Peso78 kg Calcio RuoloDifensore, centrocampista Squadra Amburgo CarrieraGiovanili 2008-2014 Osnabrück Squadre di club1 2014-2018 Sportfreunde Lotte98 (9)2018-2019 Hallescher36 (3)2019-2020 Osnabrück33 (6)2020- Amburgo85 (10)[1] 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Statistiche aggiornate all'8 aprile...

Battle during the First World War Not to be confused with Battle of the Crna Bend (1916). Battle of the Crna Bend (1917)Part of Macedonian front (World War I)Date5–9 May 1917LocationCrna LoopResult Central Powers victoryBelligerents Bulgaria Germany France Italy Russia Commanders and leaders H. von Ziegesar Karl Suren Georges Lebouc Paul Grossetti Giuseppe Pennella Mikhail Dieterichs Strength Central Powers:[1] 27 battalions 19 batteries 115 machine gun...

Royal Navy Admiral of the Fleet (1841–1920) Admiral Fisher redirects here. For other uses, see Admiral Fisher (disambiguation). Admiral of the Fleet The Right HonourableThe Lord FisherGCB, OM, GCVOFisher by Hubert von HerkomerNickname(s)JackyBorn(1841-01-25)25 January 1841Ramboda, CeylonDied10 July 1920(1920-07-10) (aged 79)London, EnglandAllegiance United KingdomService/branch Royal NavyYears of service1854–19111914–1915RankAdmiral of the FleetComman...

Nota: Para a série de televisão inspirada na história da Casa de Tudor, veja The Tudors. Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW • CAPES • Google (N • L • A)). (Fevereiro de 2021) Casa de Tudor House of Tudor (em inglês) Casa de TudorA Rosa de Tudor, uma junção da rosa vermelha e branca das casas reais Lencastre e Iorque respectivamente. Status...

Theory in social psychology Part of a series onDiscrimination Forms Institutional Structural Statistical Taste-based Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti-left handedness Anti-Masonry Ap...

French politician Portrait by Ary Scheffer, 1855 Abel-François Villemain (French pronunciation: [abɛl fʁɑ̃swa vilmɛ̃]; 9 June 1790 – 8 May 1870) was a French politician and writer. Biography Villemain was born in Paris and educated at the Lycée Louis-le-Grand. He became assistant master at the Lycée Charlemagne, and subsequently at the École Normale. In 1812 he gained a prize from the academy with an essay on Michel de Montaigne. Under the restoration he was a...